204 KiB
Uczenie maszynowe
4. Sieci neuronowe – wprowadzenie
# Przydatne importy
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline4.1. Perceptron



Pierwszy perceptron liniowy
- Frank Rosenblatt, 1957
- aparat fotograficzny podłączony do 400 fotokomórek (rozdzielczość obrazu: 20 x 20)
- wagi – potencjometry aktualizowane za pomocą silniczków
Uczenie perceptronu
Cykl uczenia perceptronu Rosenblatta:
- Sfotografuj planszę z kolejnym obiektem.
- Zaobserwuj, która lampka zapaliła się na wyjściu.
- Sprawdź, czy to jest właściwa lampka.
- Wyślij sygnał „nagrody” lub „kary”.
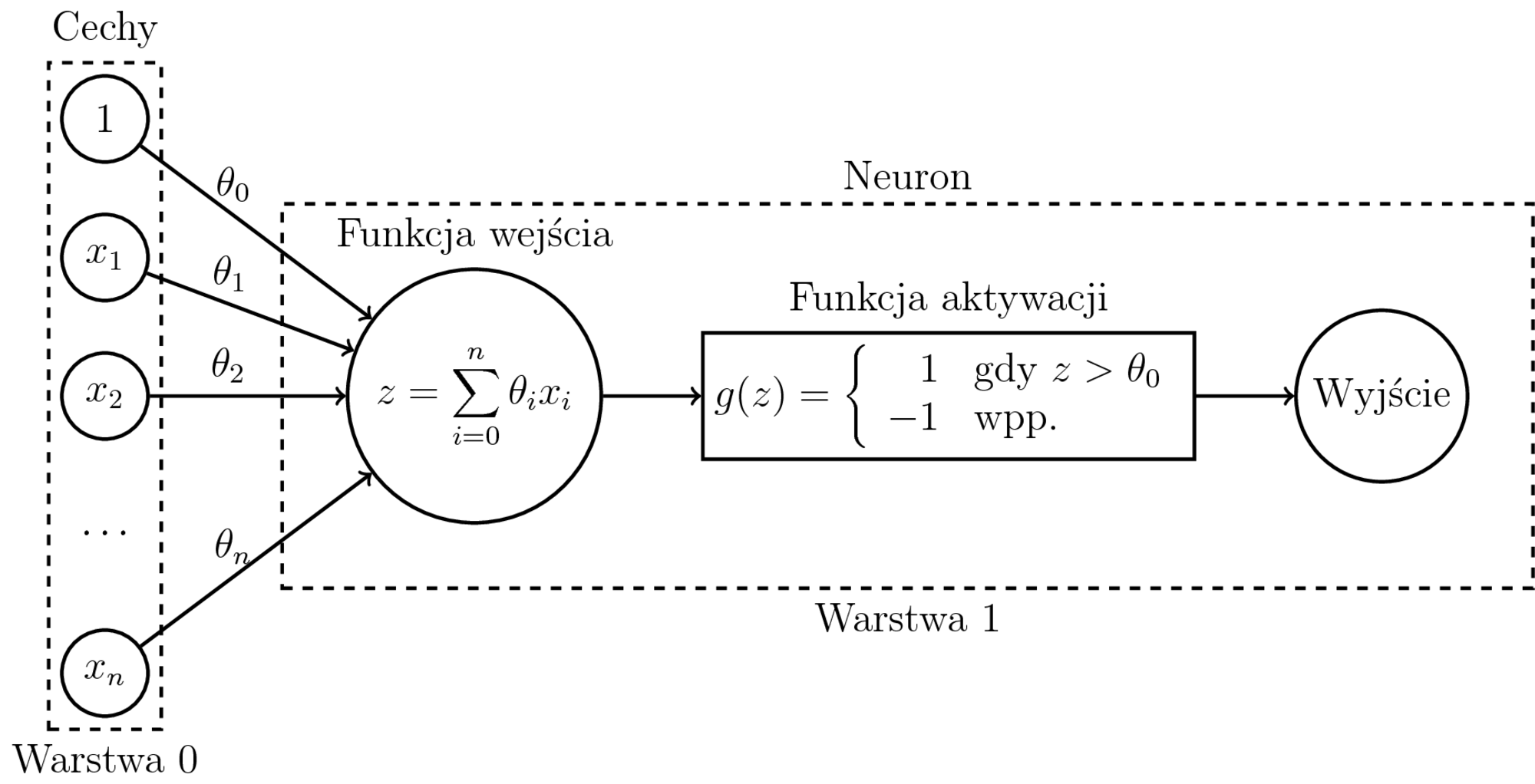
Funkcja aktywacji
Funkcja bipolarna:
$$ g(z) = \left\{ \begin{array}{rl} 1 & \textrm{gdy $z > \theta_0$} \\ -1 & \textrm{wpp.} \end{array} \right. $$
gdzie $z = \theta_0x_0 + \ldots + \theta_nx_n$,
$\theta_0$ to próg aktywacji,
$x_0 = 1$.
def bipolar_plot():
matplotlib.rcParams.update({'font.size': 16})
plt.figure(figsize=(8,5))
x = [-1,-.23,1]
y = [-1, -1, 1]
plt.ylim(-1.2,1.2)
plt.xlim(-1.2,1.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.step(x, y, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.show()bipolar_plot()Perceptron – zasada działania
- Ustal wartości początkowe $\theta$ (wektor 0 lub liczby losowe blisko 0).
- Dla każdego przykładu $(x^{(i)}, y^{(i)})$, dla $i=1,\ldots,m$
- Oblicz wartość wyjścia $o^{(i)} = g(\theta^{T}x^{(i)}) = g(\sum_{j=0}^{n} \theta_jx_j^{(i)})$
- Wykonaj aktualizację wag (tzw. _perceptron rule): $$ \theta := \theta + \Delta \theta $$ $$ \Delta \theta = \alpha(y^{(i)}-o^{(i)})x^{(i)} $$
$$\theta_j := \theta_j + \Delta \theta_j $$
Jeżeli przykład został sklasyfikowany poprawnie:
- $y^{(i)}=1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(1 - 1)x_j^{(i)} = 0$$
- $y^{(i)}=-1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(-1 - -1)x_j^{(i)} = 0$$
Czyli: jeżeli trafiłeś, to nic nie zmieniaj.
$$\theta_j := \theta_j + \Delta \theta_j $$
Jeżeli przykład został sklasyfikowany niepoprawnie:
- $y^{(i)}=1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(1 - -1)x_j^{(i)} = 2 \alpha x_j^{(i)}$$
- $y^{(i)}=-1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(-1 - 1)x_j^{(i)} = -2 \alpha x_j^{(i)}$$
Czyli: przesuń wagi w odpowiednią stronę.
Perceptron – zalety
- intuicyjny i prosty
- łatwy w implementacji
- jeżeli dane można liniowo oddzielić, algorytm jest zbieżny w skończonym czasie
Perceptron – wady
- jeżeli danych nie można oddzielić liniowo, algorytm nie jest zbieżny
def plot_perceptron():
plt.figure(figsize=(12,3))
plt.subplot(131)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.title('AND')
plt.plot([1,0,0], [0,1,0], 'ro', markersize=10)
plt.plot([1], [1], 'go', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.subplot(132)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.plot([1,0,1], [0,1,1], 'go', markersize=10)
plt.plot([0], [0], 'ro', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.title('OR')
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.subplot(133)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.title('XOR')
plt.plot([1,0], [0,1], 'go', markersize=10)
plt.plot([0,1], [0,1], 'ro', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.show()plot_perceptron()Funkcje aktywacji
Zamiast funkcji bipolarnej możemy zastosować funkcję sigmoidalną jako funkcję aktywacji.
def plot_activation_functions():
plt.figure(figsize=(16,7))
plt.subplot(121)
x = [-2,-.23,2]
y = [-1, -1, 1]
plt.ylim(-1.2,1.2)
plt.xlim(-2.2,2.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.step(x, y, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.subplot(122)
x2 = np.linspace(-2,2,100)
y2 = np.tanh(x2+ 0.23)
plt.ylim(-1.2,1.2)
plt.xlim(-2.2,2.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.plot(x2, y2, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.show()plot_activation_functions()Perceptron a regresja liniowa
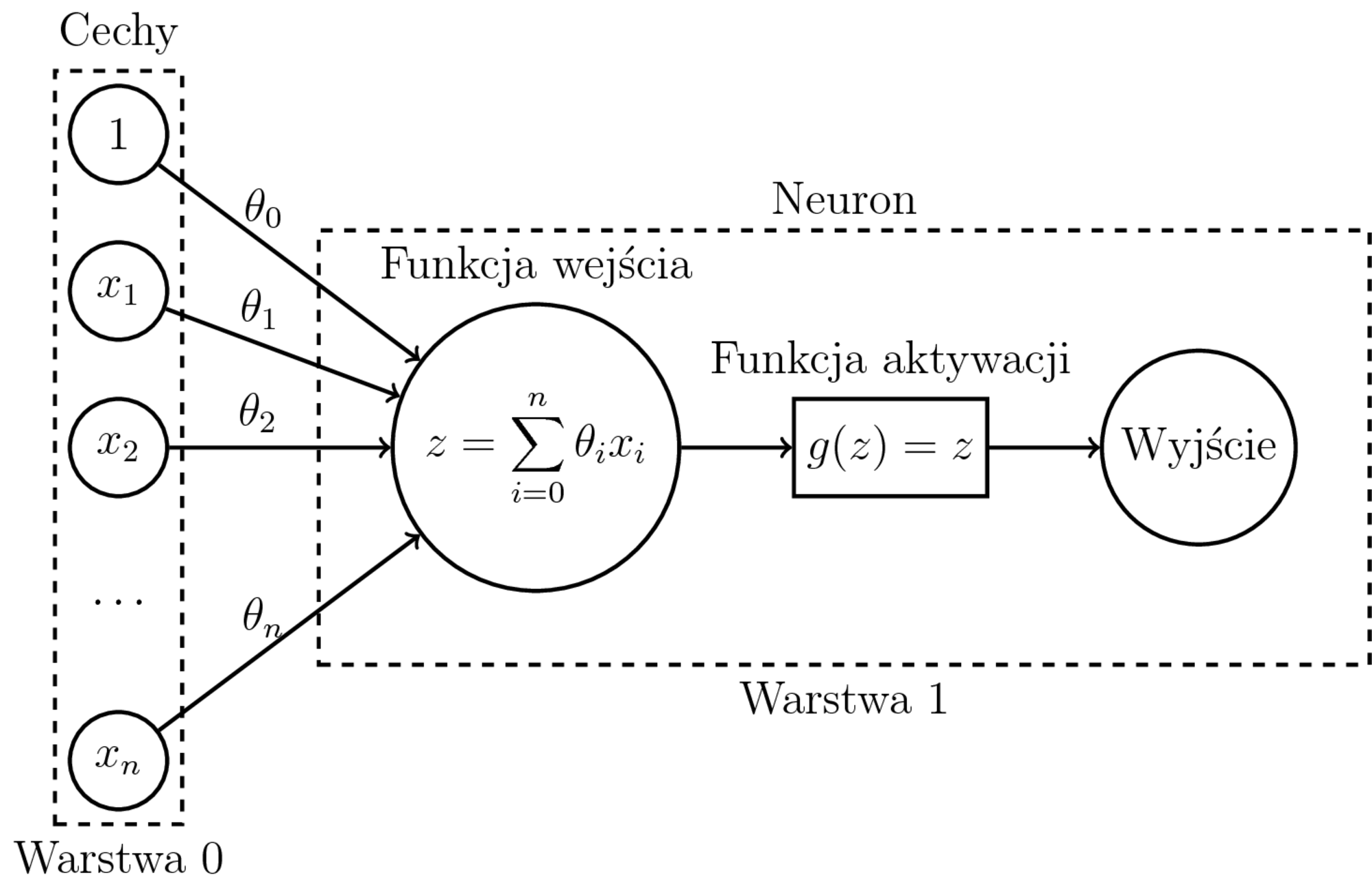
Uczenie regresji liniowej:
- Model: $$h_{\theta}(x) = \sum_{i=0}^n \theta_ix_i$$
- Funkcja kosztu (błąd średniokwadratowy): $$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$
- Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.
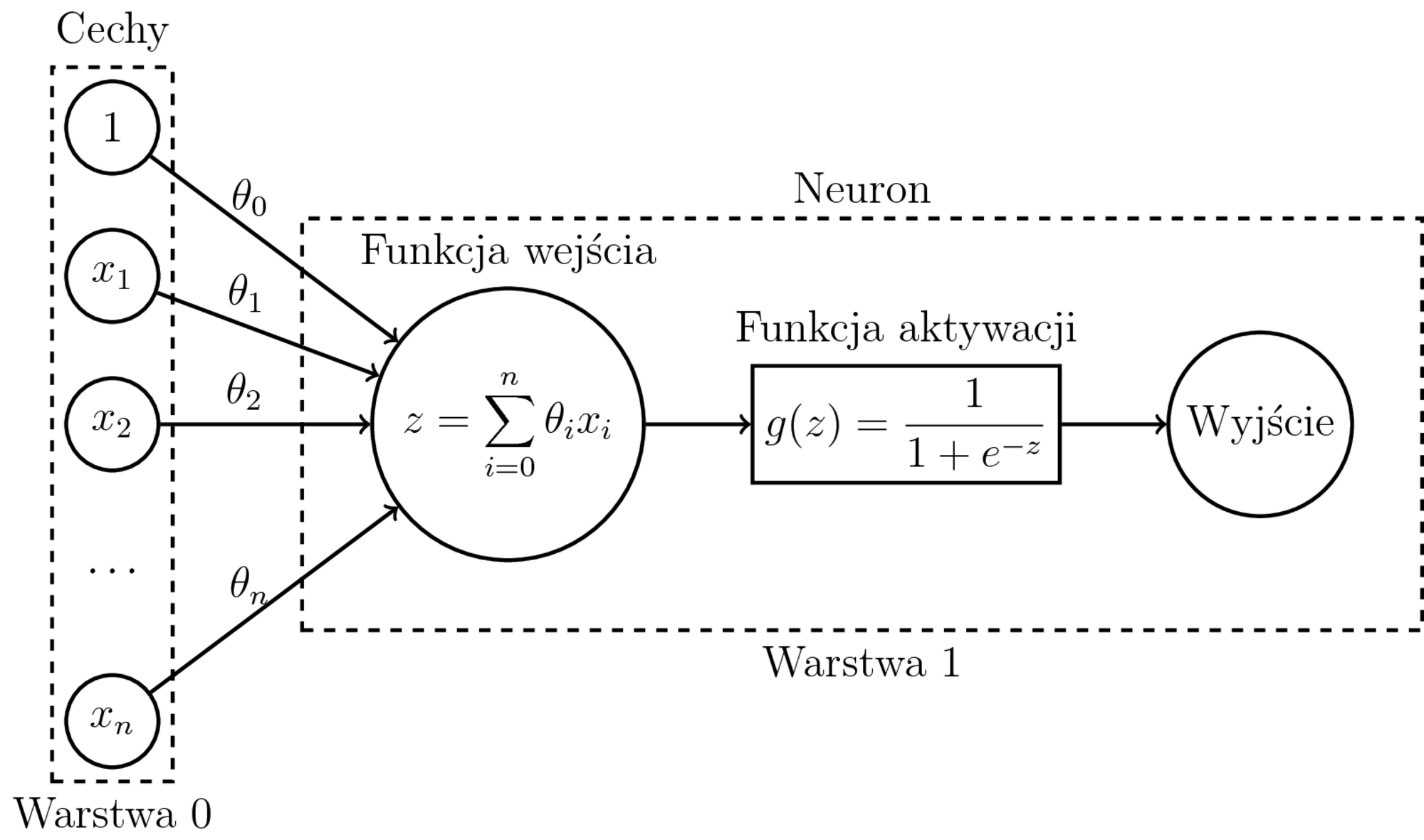
Perceptron a dwuklasowa regresja logistyczna
Uczenie dwuklasowej regresji logistycznej:
- Model: $h_{\theta}(x) = \sigma(\sum_{i=0}^n \theta_ix_i) = P(1|x,\theta)$
- Funkcja kosztu (entropia krzyżowa): $$\begin{eqnarray} J(\theta) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(1|x^{(i)},\theta) \\ && + (1-y^{(i)})\log(1-P(1|x^{(i)},\theta)) \big) \end{eqnarray}$$
- Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.
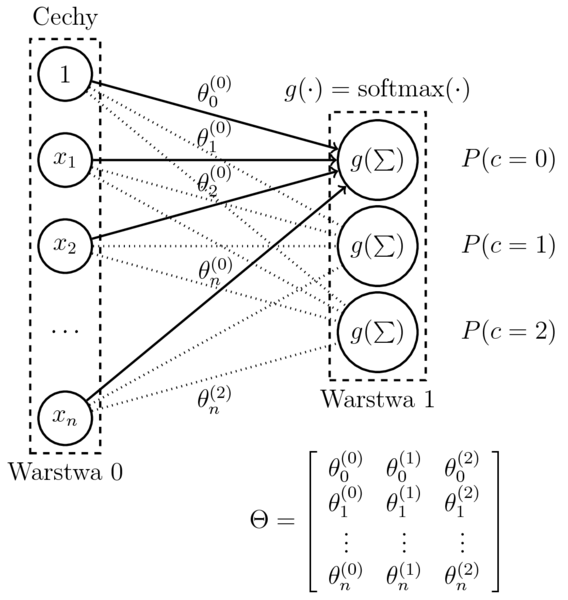
Perceptron a wieloklasowa regresja logistyczna
Wieloklasowa regresja logistyczna
- Model (dla $c$ klasyfikatorów binarnych): $$\begin{eqnarray} h_{(\theta^{(1)},\dots,\theta^{(c)})}(x) &=& \mathrm{softmax}(\sum_{i=0}^n \theta_{i}^{(1)}x_i, \ldots, \sum_{i=0}^n \theta_i^{(c)}x_i) \\ &=& \left[ P(k|x,\theta^{(1)},\dots,\theta^{(c)}) \right]_{k=1,\dots,c} \end{eqnarray}$$
- Funkcja kosztu (przymując model regresji binarnej): $$\begin{eqnarray} J(\theta^{(k)}) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(k|x^{(i)},\theta^{(k)}) \\ && + (1-y^{(i)})\log P(\neg k|x^{(i)},\theta^{(k)}) \big) \end{eqnarray}$$
- Po obliczeniu $\nabla J(\theta)$, c-krotne uruchomienie SGD, zastosowanie $\mathrm{softmax}(X)$ do niezależnie uzyskanych klasyfikatorów binarnych.
- Przyjmijmy: $$ \Theta = (\theta^{(1)},\dots,\theta^{(c)}) $$
$$h_{\Theta}(x) = \left[ P(k|x,\Theta) \right]_{k=1,\dots,c}$$
$$\delta(x,y) = \left\{\begin{array}{cl} 1 & \textrm{gdy } x=y \\ 0 & \textrm{wpp.}\end{array}\right.$$
- Wieloklasowa funkcja kosztu $J(\Theta)$ (kategorialna entropia krzyżowa): $$ J(\Theta) = -\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{c} \delta({y^{(i)},k}) \log P(k|x^{(i)},\Theta) $$
Gradient $\nabla J(\Theta)$: $$ \dfrac{\partial J(\Theta)}{\partial \Theta_{j,k}} = -\frac{1}{m}\sum_{i = 1}^{m} (\delta({y^{(i)},k}) - P(k|x^{(i)}, \Theta)) x^{(i)}_j $$
Liczymy wszystkie wagi jednym uruchomieniem SGD
Podsumowanie
- W przypadku jednowarstowej sieci neuronowej wystarczy znać gradient funkcji kosztu.
- Wtedy liczymy tak samo jak w przypadku regresji liniowej, logistycznej, wieloklasowej logistycznej itp. (wymienione modele to szczególne przypadki jednowarstwowych sieci neuronowych).
- Regresja liniowa i binarna regresja logistyczna to jeden neuron.
- Wieloklasowa regresja logistyczna to tyle neuronów, ile klas.
Funkcja aktywacji i funkcja kosztu są dobierane do problemu.
4.2. Funkcje aktywacji
- Każda funkcja aktywacji ma swoje zalety i wady.
- Różne rodzaje funkcji aktywacji nadają się do różnych zastosowań.
%matplotlib inline
import math
import matplotlib.pyplot as plt
import numpy as np
import random
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, SimpleRNN, LSTM
from keras.optimizers import Adagrad, Adam, RMSprop, SGD
from IPython.display import YouTubeVideo/home/pawel/.local/lib/python2.7/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`. from ._conv import register_converters as _register_converters Using TensorFlow backend.
def plot(fun):
x = np.arange(-3.0, 3.0, 0.01)
y = [fun(x_i) for x_i in x]
fig = plt.figure(figsize=(14, 7))
ax = fig.add_subplot(111)
fig.subplots_adjust(left=0.1, right=0.9, bottom=0.1, top=0.9)
ax.set_xlim(-3.0, 3.0)
ax.set_ylim(-1.5, 1.5)
ax.grid()
ax.plot(x, y)
plt.show()Funkcja logistyczna
$$ g(x) = \frac{1}{1 + e^{-x}} $$
- Przyjmuje wartości z przedziału $(0, 1)$.
Funkcja logistyczna – wykres
plot(lambda x: 1 / (1 + math.exp(-x)))Tangens hiperboliczny
$$ g(x) = \tanh x = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} $$
- Przyjmuje wartości z przedziału $(-1, 1)$.
- Powstaje z funkcji logistycznej przez przeskalowanie i przesunięcie.
Tangens hiperboliczny – wykres
plot(lambda x: math.tanh(x))ReLU (_Rectifier Linear Unit)
$$ g(x) = \max(0, x) $$
ReLU – zalety
- Mniej podatna na problem zanikającego gradientu (_vanishing gradient) niż funkcje sigmoidalne, dzięki czemu SGD jest szybciej zbieżna.
- Prostsze obliczanie gradientu.
- Dzięki zerowaniu ujemnych wartości, wygasza neurony, „rozrzedzając” sieć (_sparsity), co przyspiesza obliczenia.
ReLU – wady
- Dla dużych wartości gradient może „eksplodować”.
- „Wygaszanie” neuronów.
ReLU – wykres
plot(lambda x: max(0, x))Softplus
$$ g(x) = \log(1 + e^{x}) $$
- Wygładzona wersja ReLU.
Softplus – wykres
plot(lambda x: math.log(1 + math.exp(x)))Problem zanikającego gradientu (_vanishing gradient problem)
- Sigmoidalne funkcje aktywacji ograniczają wartości na wyjściach neuronów do niewielkich przedziałów ($(-1, 1)$, $(0, 1)$ itp.).
- Jeżeli sieć ma wiele warstw, to podczas propagacji wstecznej mnożymy przez siebie wiele małych wartości → obliczony gradient jest mały.
- Im więcej warstw, tym silniejszy efekt zanikania.
Sposoby na zanikający gradient
- Modyfikacja algorytmu optymalizacji (_RProp, RMSProp)
- Użycie innej funckji aktywacji (ReLU, softplus)
- Dodanie warstw _dropout
- Nowe architektury (LSTM itp.)
- Więcej danych, zwiększenie mocy obliczeniowej
4.3. Wielowarstwowe sieci neuronowe
czyli _Artificial Neural Networks (ANN) lub Multi-Layer Perceptrons (MLP)
Architektura sieci
- Sieć neuronowa jako graf neuronów.
- Organizacja sieci przez warstwy.
- Najczęściej stosowane są sieci jednokierunkowe i gęste.
- $n$-warstwowa sieć neuronowa ma $n+1$ warstw (nie liczymy wejścia).
- Rozmiary sieci określane poprzez liczbę neuronów lub parametrów.
Sieć neuronowa jednokierunkowa (_feedforward)
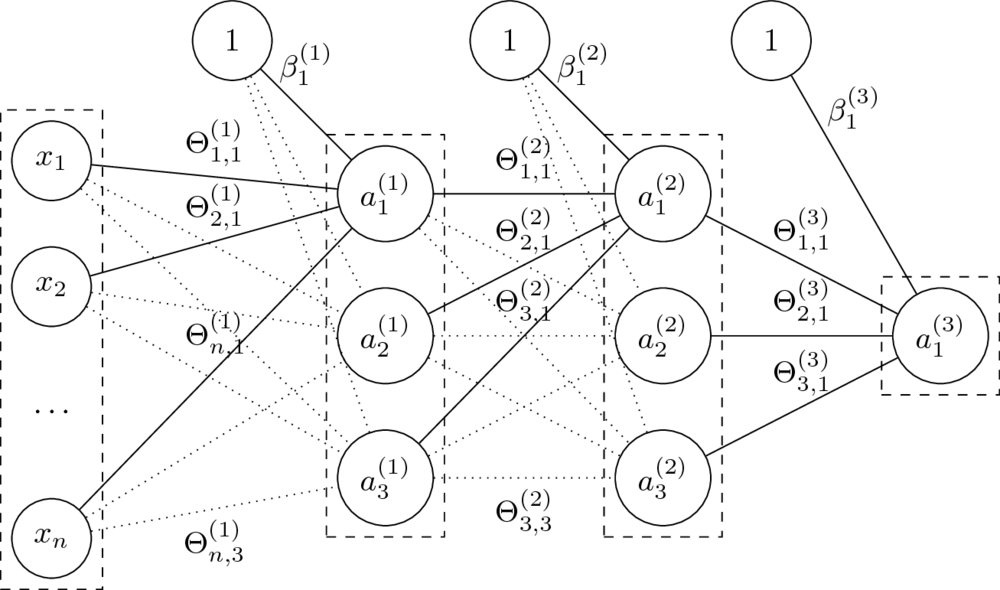
- Mając daną $n$-warstwową sieć neuronową oraz jej parametry $\Theta^{(1)}, \ldots, \Theta^{(L)} $ oraz $\beta^{(1)}, \ldots, \beta^{(L)} $ liczymy:
$$a^{(l)} = g^{(l)}\left( a^{(l-1)} \Theta^{(l)} + \beta^{(l)} \right). $$
- Funkcje $g^{(l)}$ to tzw. funkcje aktywacji.
Dla $i = 0$ przyjmujemy $a^{(0)} = \mathrm{x}$ (wektor wierszowy cech) oraz $g^{(0)}(x) = x$ (identyczność).
- Parametry $\Theta$ to wagi na połączeniach miedzy neuronami dwóch warstw.
Rozmiar macierzy $\Theta^{(l)}$, czyli macierzy wag na połączeniach warstw $a^{(l-1)}$ i $a^{(l)}$, to $\dim(a^{(l-1)}) \times \dim(a^{(l)})$.
- Parametry $\beta$ zastępują tutaj dodawanie kolumny z jedynkami do macierzy cech.
Macierz $\beta^{(l)}$ ma rozmiar równy liczbie neuronów w odpowiedniej warstwie, czyli $1 \times \dim(a^{(l)})$.
- Klasyfikacja: dla ostatniej warstwy $L$ (o rozmiarze równym liczbie klas) przyjmuje się $g^{(L)}(x) = \mathop{\mathrm{softmax}}(x)$.
- Regresja: pojedynczy neuron wyjściowy jak na obrazku. Funkcją aktywacji może wtedy być np. funkcja identycznościowa.
- Pozostałe funkcje aktywacji najcześciej mają postać sigmoidy, np. sigmoidalna, tangens hiperboliczny.
- Mogą mieć też inny kształt, np. ReLU, leaky ReLU, maxout.
Jak uczyć sieci neuronowe?
- W poznanych do tej pory algorytmach (regresja liniowa, regresja logistyczna) do uczenia używaliśmy funkcji kosztu, jej gradientu oraz algorytmu gradientu prostego (GD/SGD)
- Dla sieci neuronowych potrzebowalibyśmy również znaleźć gradient funkcji kosztu.
- Sprowadza się to do bardziej ogólnego problemu:
jak obliczyć gradient $\nabla f(x)$ dla danej funkcji $f$ i wektora wejściowego $x$?
4.4. Metoda propagacji wstecznej – wprowadzenie
Pochodna funkcji
- Pochodna mierzy, jak szybko zmienia się wartość funkcji względem zmiany jej argumentów:
$$ \frac{d f(x)}{d x} = \lim_{h \to 0} \frac{ f(x + h) - f(x) }{ h } $$
Pochodna cząstkowa i gradient
- Pochodna cząstkowa mierzy, jak szybko zmienia się wartość funkcji względem zmiany jej _pojedynczego argumentu.
- Gradient to wektor pochodnych cząstkowych:
$$ \nabla f = \left( \frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right) $$
Gradient – przykłady
$$ f(x_1, x_2) = x_1 + x_2 \qquad \to \qquad \frac{\partial f}{\partial x_1} = 1, \quad \frac{\partial f}{\partial x_2} = 1, \quad \nabla f = (1, 1) $$
$$ f(x_1, x_2) = x_1 \cdot x_2 \qquad \to \qquad \frac{\partial f}{\partial x_1} = x_2, \quad \frac{\partial f}{\partial x_2} = x_1, \quad \nabla f = (x_2, x_1) $$
$$ f(x_1, x_2) = \max(x_1 + x_2) \hskip{12em} \\ \to \qquad \frac{\partial f}{\partial x_1} = \mathbb{1}_{x \geq y}, \quad \frac{\partial f}{\partial x_2} = \mathbb{1}{y \geq x}, \quad \nabla f = (\mathbb{1}{x \geq y}, \mathbb{1}{y \geq x}) $$
Własności pochodnych cząstkowych
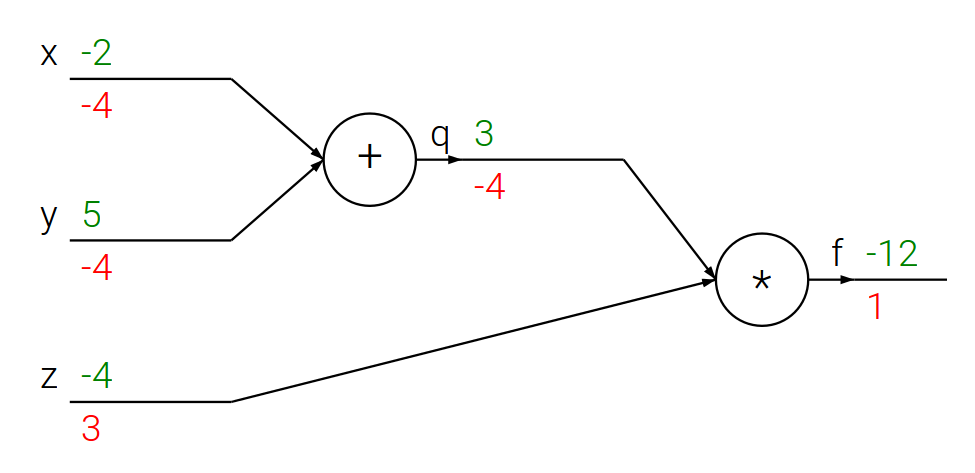
Jezeli $f(x, y, z) = (x + y) , z$ oraz $x + y = q$, to: $$f = q z, \quad \frac{\partial f}{\partial q} = z, \quad \frac{\partial f}{\partial z} = q, \quad \frac{\partial q}{\partial x} = 1, \quad \frac{\partial q}{\partial y} = 1 $$
Reguła łańcuchowa
$$ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} , \frac{\partial q}{\partial x}, \quad \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} , \frac{\partial q}{\partial y} $$
Propagacja wsteczna – prosty przykład
# Dla ustalonego wejścia
x = -2; y = 5; z = -4# Krok w przód
q = x + y
f = q * z
print(q, f)(3, -12)
# Propagacja wsteczna dla f = q * z
dz = q
dq = z
# Propagacja wsteczna dla q = x + y
dx = 1 * dq # z reguły łańcuchowej
dy = 1 * dq # z reguły łańcuchowej
print([dx, dy, dz])[-4, -4, 3]
- Właśnie tak wygląda obliczanie pochodnych metodą propagacji wstecznej!
- Spróbujmy czegoś bardziej skomplikowanego:
metodą propagacji wstecznej obliczmy pochodną funkcji sigmoidalnej.
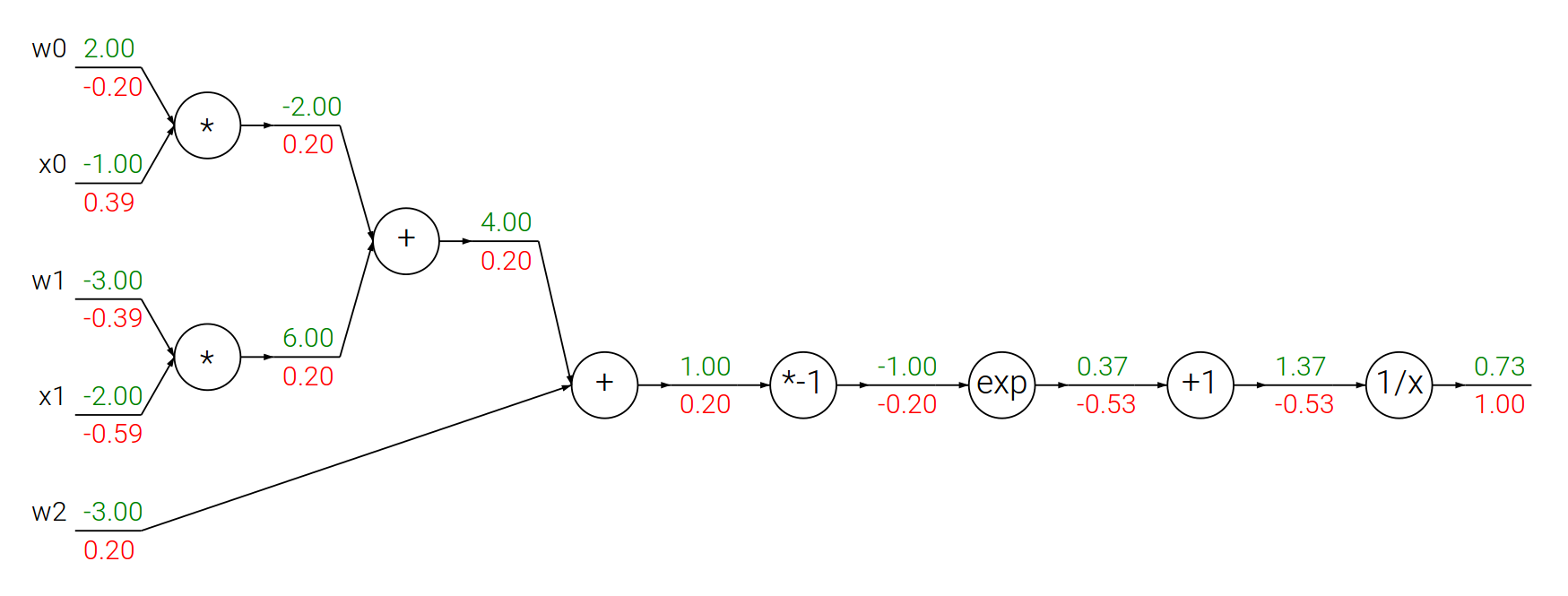
Propagacja wsteczna – funkcja sigmoidalna
Funkcja sigmoidalna:
$$f(\theta,x) = \frac{1}{1+e^{-(\theta_0 x_0 + \theta_1 x_1 + \theta_2)}}$$
$$ \begin{array}{lcl} f(x) = \frac{1}{x} \quad & \rightarrow & \quad \frac{df}{dx} = -\frac{1}{x^2} \\ f_c(x) = c + x \quad & \rightarrow & \quad \frac{df}{dx} = 1 \\ f(x) = e^x \quad & \rightarrow & \quad \frac{df}{dx} = e^x \\ f_a(x) = ax \quad & \rightarrow & \quad \frac{df}{dx} = a \\ \end{array} $$
# Losowe wagi i dane
w = [2,-3,-3]
x = [-1, -2]
# Krok w przód
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # funkcja sigmoidalna
# Krok w tył
ddot = (1 - f) * f # pochodna funkcji sigmoidalnej
dx = [w[0] * ddot, w[1] * ddot]
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot]
print(dx)
print(dw)[0.3932238664829637, -0.5898357997244456] [-0.19661193324148185, -0.3932238664829637, 0.19661193324148185]
Obliczanie gradientów – podsumowanie
- Gradient $f$ dla $x$ mówi, jak zmieni się całe wyrażenie przy zmianie wartości $x$.
- Gradienty łączymy, korzystając z reguły łańcuchowej.
- W kroku "wstecz" gradienty informują, które części grafu powinny być zwiększone lub zmniejszone (i z jaką siłą), aby zwiększyć wartość na wyjściu.
- W kontekście implementacji chcemy dzielić funkcję $f$ na części, dla których można łatwo obliczyć gradienty.
4.5. Uczenie wielowarstwowych sieci neuronowych metodą propagacji wstecznej
Mając algorytm SGD oraz gradienty wszystkich wag, moglibyśmy trenować każdą sieć.
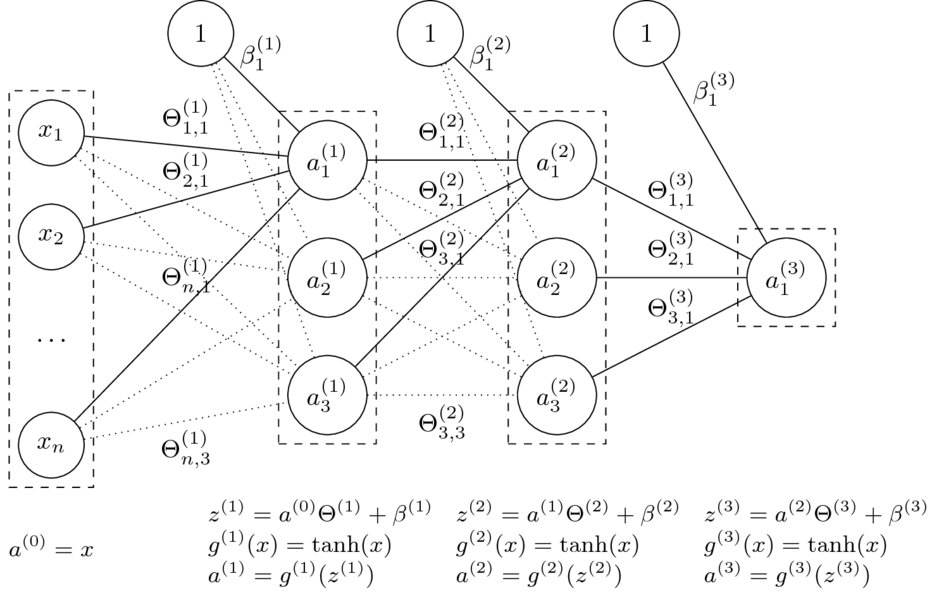
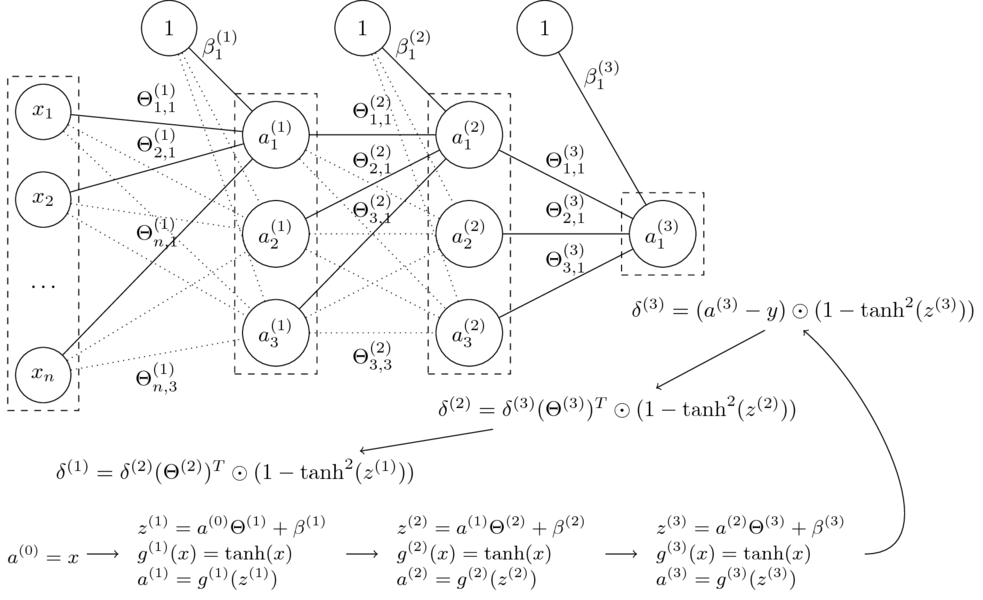
- Niech $\Theta = (\Theta^{(1)},\Theta^{(2)},\Theta^{(3)},\beta^{(1)},\beta^{(2)},\beta^{(3)})$
- Funkcja sieci neuronowej z grafiki: $$\small h_\Theta(x) = \tanh(\tanh(\tanh(x\Theta^{(1)}+\beta^{(1)})\Theta^{(2)} + \beta^{(2)})\Theta^{(3)} + \beta^{(3)})$$
- Funkcja kosztu dla regresji: $$J(\Theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h_\Theta(x^{(i)})- y^{(i)})^2 $$
- Jak obliczymy gradienty?
$$\nabla_{\Theta^{(l)}} J(\Theta) = ? \quad \nabla_{\beta^{(l)}} J(\Theta) = ?$$
W kierunku propagacji wstecznej
- Pewna (niewielka) zmiana wagi $\Delta z^l_j$ dla $j$-ego neuronu w warstwie $l$ pociąga za sobą (niewielką) zmianę kosztu:
$$\frac{\partial J(\Theta)}{\partial z^{l}_j} \Delta z^{l}_j$$
- Jeżeli $\frac{\partial J(\Theta)}{\partial z^{l}_j}$ jest duża, $\Delta z^l_j$ ze znakiem przeciwnym zredukuje koszt.
- Jeżeli $\frac{\partial J(\Theta)}{\partial z^l_j}$ jest bliska zeru, koszt nie będzie mocno poprawiony.
- Definiujemy błąd $\delta^l_j$ neuronu $j$ w warstwie $l$:
$$\delta^l_j := \dfrac{\partial J(\Theta)}{\partial z^l_j}$$ $$\delta^l := \nabla_{z^l} J(\Theta) \quad \textrm{ (zapis wektorowy)} $$
Podstawowe równania propagacji wstecznej
$$ \begin{array}{rcll} \delta^L & = & \nabla_{a^L}J(\Theta) \odot { \left( g^{L} \right) }^{\prime} \left( z^L \right) & (BP1) \\[2mm] \delta^{l} & = & \left( \left( \Theta^{l+1} \right) ! ^\top , \delta^{l+1} \right) \odot {{ \left( g^{l} \right) }^{\prime}} \left( z^{l} \right) & (BP2)\\[2mm] \nabla_{\beta^l} J(\Theta) & = & \delta^l & (BP3)\\[2mm] \nabla_{\Theta^l} J(\Theta) & = & a^{l-1} \odot \delta^l & (BP4)\\ \end{array} $$
(BP1)
$$ \delta^L_j ; = ; \frac{ \partial J }{ \partial a^L_j } , g' !! \left( z^L_j \right) $$ $$ \delta^L ; = ; \nabla_{a^L}J(\Theta) \odot { \left( g^{L} \right) }^{\prime} \left( z^L \right) $$ Błąd w ostatniej warstwie jest iloczynem szybkości zmiany kosztu względem $j$-tego wyjścia i szybkości zmiany funkcji aktywacji w punkcie $z^L_j$.
(BP2)
$$ \delta^{l} ; = ; \left( \left( \Theta^{l+1} \right) ! ^\top , \delta^{l+1} \right) \odot {{ \left( g^{l} \right) }^{\prime}} \left( z^{l} \right) $$ Aby obliczyć błąd w $l$-tej warstwie, należy przemnożyć błąd z następnej ($(l+1)$-szej) warstwy przez transponowany wektor wag, a uzyskaną macierz pomnożyć po współrzędnych przez szybkość zmiany funkcji aktywacji w punkcie $z^l$.
(BP3)
$$ \nabla_{\beta^l} J(\Theta) ; = ; \delta^l $$ Błąd w $l$-tej warstwie jest równy wartości gradientu funkcji kosztu.
(BP4)
$$ \nabla_{\Theta^l} J(\Theta) ; = ; a^{l-1} \odot \delta^l $$ Gradient funkcji kosztu względem wag $l$-tej warstwy można obliczyć jako iloczyn po współrzędnych $a^{l-1}$ przez $\delta^l$.
Algorytm propagacji wstecznej
Dla pojedynczego przykładu $(x,y)$:
- Wejście: Ustaw aktywacje w warstwie cech $a^{(0)}=x$
- Feedforward: dla $l=1,\dots,L$ oblicz $z^{(l)} = a^{(l-1)} \Theta^{(l)} + \beta^{(l)}$ oraz $a^{(l)}=g^{(l)} !! \left( z^{(l)} \right)$
- Błąd wyjścia $\delta^{(L)}$: oblicz wektor $$\delta^{(L)}= \nabla_{a^{(L)}}J(\Theta) \odot {g^{\prime}}^{(L)} !! \left( z^{(L)} \right) $$
- Propagacja wsteczna błędu: dla $l = L-1,L-2,\dots,1$ oblicz $$\delta^{(l)} = \delta^{(l+1)}(\Theta^{(l+1)})^T \odot {g^{\prime}}^{(l)} !! \left( z^{(l)} \right) $$
- Gradienty:
- $\dfrac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = a_i^{(l-1)}\delta_j^{(l)} \textrm{ oraz } \dfrac{\partial}{\partial \beta_{j}^{(l)}} J(\Theta) = \delta_j^{(l)}$
W naszym przykładzie:
$$\small J(\Theta) = \frac{1}{2} \left( a^{(L)} - y \right) ^2 $$ $$\small \dfrac{\partial}{\partial a^{(L)}} J(\Theta) = a^{(L)} - y$$
$$\small \tanh^{\prime}(x) = 1 - \tanh^2(x)$$
Algorytm SGD z propagacją wsteczną
Pojedyncza iteracja:
- Dla parametrów $\Theta = (\Theta^{(1)},\ldots,\Theta^{(L)})$ utwórz pomocnicze macierze zerowe $\Delta = (\Delta^{(1)},\ldots,\Delta^{(L)})$ o takich samych wymiarach (dla uproszczenia opuszczono wagi $\beta$).
- Dla $m$ przykładów we wsadzie (_batch), $i = 1,\ldots,m$:
- Wykonaj algortym propagacji wstecznej dla przykładu $(x^{(i)}, y^{(i)})$ i przechowaj gradienty $\nabla_{\Theta}J^{(i)}(\Theta)$ dla tego przykładu;
- $\Delta := \Delta + \dfrac{1}{m}\nabla_{\Theta}J^{(i)}(\Theta)$
- Wykonaj aktualizację wag: $\Theta := \Theta - \alpha \Delta$
Propagacja wsteczna – podsumowanie
- Algorytm pierwszy raz wprowadzony w latach 70. XX w.
- W 1986 David Rumelhart, Geoffrey Hinton i Ronald Williams pokazali, że jest znacznie szybszy od wcześniejszych metod.
- Obecnie najpopularniejszy algorytm uczenia sieci neuronowych.
4.6. Przykłady implementacji wielowarstwowych sieci neuronowych
Uwaga!
Poniższe przykłady wykorzystują interfejs Keras, który jest częścią biblioteki TensorFlow.
Aby uruchomić TensorFlow w środowisku Jupyter, należy wykonać następujące czynności:
Przed pierwszym uruchomieniem (wystarczy wykonać tylko raz)
Instalacja biblioteki TensorFlow w środowisku Anaconda:
- Uruchom _Anaconda Navigator
- Wybierz kafelek _CMD.exe Prompt
- Kliknij przycisk _Launch
- Pojawi się konsola. Wpisz następujące polecenia, każde zatwierdzając wciśnięciem klawisza Enter:
conda create -n tf tensorflow conda activate tf conda install pandas matplotlib jupyter notebook
Przed każdym uruchomieniem
Jeżeli chcemy korzystać z biblioteki TensorFlow, to środowisko Jupyter Notebook należy uruchomić w następujący sposób:
- Uruchom _Anaconda Navigator
- Wybierz kafelek _CMD.exe Prompt
- Kliknij przycisk _Launch
- Pojawi się konsola. Wpisz następujące polecenia, każde zatwierdzając wciśnięciem klawisza Enter:
conda activate tf jupyter notebook
Przykład: MNIST
_Modified National Institute of Standards and Technology database
- Zbiór cyfr zapisanych pismem odręcznym
- 60 000 przykładów uczących, 10 000 przykładów testowych
- Rozdzielczość każdego przykładu: 28 × 28 = 784 piksele
# źródło: https://github.com/keras-team/keras/examples/minst_mlp.py
from tensorflow import keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense, Dropout
# załaduj dane i podziel je na zbiory uczący i testowy
(x_train, y_train), (x_test, y_test) = mnist.load_data()from matplotlib import pyplot as plt
def draw_examples(examples, captions=None):
plt.figure(figsize=(16, 4))
m = len(examples)
for i, example in enumerate(examples):
plt.subplot(100 + m * 10 + i + 1)
plt.imshow(example, cmap=plt.get_cmap('gray'))
plt.show()
if captions is not None:
print(6 * ' ' + (10 * ' ').join(str(captions[i]) for i in range(m)))draw_examples(x_train[:7], captions=y_train)5 0 4 1 9 2 1
num_classes = 10
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('{} przykładów uczących'.format(x_train.shape[0]))
print('{} przykładów testowych'.format(x_test.shape[0]))
# przekonwertuj wektory klas na binarne macierze klas
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)60000 przykładów uczących 10000 przykładów testowych
model = keras.Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
model.summary()Model: "sequential_21" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_59 (Dense) (None, 512) 401920 _________________________________________________________________ dropout_2 (Dropout) (None, 512) 0 _________________________________________________________________ dense_60 (Dense) (None, 512) 262656 _________________________________________________________________ dropout_3 (Dropout) (None, 512) 0 _________________________________________________________________ dense_61 (Dense) (None, 10) 5130 ================================================================= Total params: 669,706 Trainable params: 669,706 Non-trainable params: 0 _________________________________________________________________
print(x_train.shape, y_train.shape)(60000, 784) (60000, 10)
model.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.RMSprop(), metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=128, epochs=5, verbose=1,
validation_data=(x_test, y_test))Epoch 1/5 469/469 [==============================] - 11s 23ms/step - loss: 0.2463 - accuracy: 0.9238 - val_loss: 0.1009 - val_accuracy: 0.9690 Epoch 2/5 469/469 [==============================] - 10s 22ms/step - loss: 0.1042 - accuracy: 0.9681 - val_loss: 0.0910 - val_accuracy: 0.9739 Epoch 3/5 469/469 [==============================] - 11s 23ms/step - loss: 0.0774 - accuracy: 0.9762 - val_loss: 0.0843 - val_accuracy: 0.9755 Epoch 4/5 469/469 [==============================] - 11s 24ms/step - loss: 0.0606 - accuracy: 0.9815 - val_loss: 0.0691 - val_accuracy: 0.9818 Epoch 5/5 469/469 [==============================] - 10s 22ms/step - loss: 0.0504 - accuracy: 0.9848 - val_loss: 0.0886 - val_accuracy: 0.9772
<tensorflow.python.keras.callbacks.History at 0x1ed6e0565b0>
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))Test loss: 0.08859136700630188 Test accuracy: 0.9771999716758728
Warstwa _dropout to metoda regularyzacji, służy zapobieganiu nadmiernemu dopasowaniu sieci. Polega na tym, że część węzłów sieci jest usuwana w sposób losowy.
# Bez warstw Dropout
num_classes = 10
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model_no_dropout = keras.Sequential()
model_no_dropout.add(Dense(512, activation='relu', input_shape=(784,)))
model_no_dropout.add(Dense(512, activation='relu'))
model_no_dropout.add(Dense(num_classes, activation='softmax'))
model_no_dropout.summary()
model_no_dropout.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.RMSprop(),
metrics=['accuracy'])
model_no_dropout.fit(x_train, y_train,
batch_size=128,
epochs=5,
verbose=1,
validation_data=(x_test, y_test))Model: "sequential_22" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_62 (Dense) (None, 512) 401920 _________________________________________________________________ dense_63 (Dense) (None, 512) 262656 _________________________________________________________________ dense_64 (Dense) (None, 10) 5130 ================================================================= Total params: 669,706 Trainable params: 669,706 Non-trainable params: 0 _________________________________________________________________ Epoch 1/5 469/469 [==============================] - 10s 20ms/step - loss: 0.2203 - accuracy: 0.9317 - val_loss: 0.0936 - val_accuracy: 0.9697 Epoch 2/5 469/469 [==============================] - 10s 21ms/step - loss: 0.0816 - accuracy: 0.9746 - val_loss: 0.0747 - val_accuracy: 0.9779 Epoch 3/5 469/469 [==============================] - 10s 20ms/step - loss: 0.0544 - accuracy: 0.9827 - val_loss: 0.0674 - val_accuracy: 0.9798 Epoch 4/5 469/469 [==============================] - 10s 22ms/step - loss: 0.0384 - accuracy: 0.9879 - val_loss: 0.0746 - val_accuracy: 0.9806 Epoch 5/5 469/469 [==============================] - 10s 22ms/step - loss: 0.0298 - accuracy: 0.9901 - val_loss: 0.0736 - val_accuracy: 0.9801
<tensorflow.python.keras.callbacks.History at 0x1ed7eba8070>
# Bez warstw Dropout
score = model_no_dropout.evaluate(x_test, y_test, verbose=0)
print('Test loss (no dropout): {}'.format(score[0]))
print('Test accuracy (no dropout): {}'.format(score[1]))Test loss (no dropout): 0.07358124107122421 Test accuracy (no dropout): 0.9800999760627747
# Więcej warstw, inna funkcja aktywacji
num_classes = 10
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model3 = keras.Sequential()
model3.add(Dense(2500, activation='tanh', input_shape=(784,)))
model3.add(Dense(2000, activation='tanh'))
model3.add(Dense(1500, activation='tanh'))
model3.add(Dense(1000, activation='tanh'))
model3.add(Dense(500, activation='tanh'))
model3.add(Dense(num_classes, activation='softmax'))
model3.summary()
model3.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.RMSprop(),
metrics=['accuracy'])
model3.fit(x_train, y_train,
batch_size=128,
epochs=10,
verbose=1,
validation_data=(x_test, y_test))Model: "sequential_23" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_65 (Dense) (None, 2500) 1962500 _________________________________________________________________ dense_66 (Dense) (None, 2000) 5002000 _________________________________________________________________ dense_67 (Dense) (None, 1500) 3001500 _________________________________________________________________ dense_68 (Dense) (None, 1000) 1501000 _________________________________________________________________ dense_69 (Dense) (None, 500) 500500 _________________________________________________________________ dense_70 (Dense) (None, 10) 5010 ================================================================= Total params: 11,972,510 Trainable params: 11,972,510 Non-trainable params: 0 _________________________________________________________________ Epoch 1/10 469/469 [==============================] - 129s 275ms/step - loss: 0.9587 - accuracy: 0.7005 - val_loss: 0.5066 - val_accuracy: 0.8566 Epoch 2/10 469/469 [==============================] - 130s 276ms/step - loss: 0.2666 - accuracy: 0.9234 - val_loss: 0.3376 - val_accuracy: 0.9024 Epoch 3/10 469/469 [==============================] - 130s 277ms/step - loss: 0.1811 - accuracy: 0.9477 - val_loss: 0.1678 - val_accuracy: 0.9520 Epoch 4/10 469/469 [==============================] - 134s 287ms/step - loss: 0.1402 - accuracy: 0.9588 - val_loss: 0.1553 - val_accuracy: 0.9576 Epoch 5/10 469/469 [==============================] - 130s 278ms/step - loss: 0.1153 - accuracy: 0.9662 - val_loss: 0.1399 - val_accuracy: 0.9599 Epoch 6/10 469/469 [==============================] - 130s 277ms/step - loss: 0.0956 - accuracy: 0.9711 - val_loss: 0.1389 - val_accuracy: 0.9612 Epoch 7/10 469/469 [==============================] - 131s 280ms/step - loss: 0.0803 - accuracy: 0.9761 - val_loss: 0.1008 - val_accuracy: 0.9724 Epoch 8/10 469/469 [==============================] - 134s 286ms/step - loss: 0.0685 - accuracy: 0.9797 - val_loss: 0.1137 - val_accuracy: 0.9679 Epoch 9/10 469/469 [==============================] - 130s 278ms/step - loss: 0.0602 - accuracy: 0.9819 - val_loss: 0.1064 - val_accuracy: 0.9700 Epoch 10/10 469/469 [==============================] - 129s 274ms/step - loss: 0.0520 - accuracy: 0.9843 - val_loss: 0.1095 - val_accuracy: 0.9698
<tensorflow.python.keras.callbacks.History at 0x1ed0e628250>
# Więcej warstw, inna funkcja aktywacji
score = model3.evaluate(x_test, y_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))Test loss: 0.10945799201726913 Test accuracy: 0.9697999954223633
Przykład: 4-pikselowy aparat fotograficzny
def generate_example(description):
variant = random.choice([1, -1])
if description == 's': # solid
return (np.array([[ 1.0, 1.0], [ 1.0, 1.0]]) if variant == 1 else
np.array([[-1.0, -1.0], [-1.0, -1.0]]))
elif description == 'v': # vertical
return (np.array([[ 1.0, -1.0], [ 1.0, -1.0]]) if variant == 1 else
np.array([[-1.0, 1.0], [-1.0, 1.0]]))
elif description == 'd': # diagonal
return (np.array([[ 1.0, -1.0], [-1.0, 1.0]]) if variant == 1 else
np.array([[-1.0, 1.0], [ 1.0, -1.0]]))
elif description == 'h': # horizontal
return (np.array([[ 1.0, 1.0], [-1.0, -1.0]]) if variant == 1 else
np.array([[-1.0, -1.0], [ 1.0, 1.0]]))
else:
return np.array([[random.uniform(-1, 1), random.uniform(-1, 1)],
[random.uniform(-1, 1), random.uniform(-1, 1)]])import random
num_classes = 4
trainset_size = 4000
testset_size = 1000
y4_train = np.array([random.choice(['s', 'v', 'd', 'h']) for i in range(trainset_size)])
x4_train = np.array([generate_example(desc) for desc in y4_train])
y4_test = np.array([random.choice(['s', 'v', 'd', 'h']) for i in range(testset_size)])
x4_test = np.array([generate_example(desc) for desc in y4_test])draw_examples(x4_train[:7], captions=y4_train)s d h s d v v
x4_train = x4_train.reshape(trainset_size, 4)
x4_test = x4_test.reshape(testset_size, 4)
x4_train = x4_train.astype('float32')
x4_test = x4_test.astype('float32')
y4_train = np.array([{'s': 0, 'v': 1, 'd': 2, 'h': 3}[desc] for desc in y4_train])
y4_test = np.array([{'s': 0, 'v': 1, 'd': 2, 'h': 3}[desc] for desc in y4_test])
y4_train = keras.utils.to_categorical(y4_train, num_classes)
y4_test = keras.utils.to_categorical(y4_test, num_classes)model4 = keras.Sequential()
model4.add(Dense(4, activation='tanh', input_shape=(4,)))
model4.add(Dense(4, activation='tanh'))
model4.add(Dense(8, activation='relu'))
model4.add(Dense(num_classes, activation='softmax'))
model4.summary()Model: "sequential_24" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_71 (Dense) (None, 4) 20 _________________________________________________________________ dense_72 (Dense) (None, 4) 20 _________________________________________________________________ dense_73 (Dense) (None, 8) 40 _________________________________________________________________ dense_74 (Dense) (None, 4) 36 ================================================================= Total params: 116 Trainable params: 116 Non-trainable params: 0 _________________________________________________________________
model4.layers[0].set_weights(
[np.array([[ 1.0, 0.0, 1.0, 0.0],
[ 0.0, 1.0, 0.0, 1.0],
[ 1.0, 0.0, -1.0, 0.0],
[ 0.0, 1.0, 0.0, -1.0]],
dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])
model4.layers[1].set_weights(
[np.array([[ 1.0, -1.0, 0.0, 0.0],
[ 1.0, 1.0, 0.0, 0.0],
[ 0.0, 0.0, 1.0, -1.0],
[ 0.0, 0.0, -1.0, -1.0]],
dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])
model4.layers[2].set_weights(
[np.array([[ 1.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[ 0.0, 0.0, 1.0, -1.0, 0.0, 0.0, 0.0, 0.0],
[ 0.0, 0.0, 0.0, 0.0, 1.0, -1.0, 0.0, 0.0],
[ 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, -1.0]],
dtype=np.float32), np.array([0., 0., 0., 0., 0., 0., 0., 0.], dtype=np.float32)])model4.layers[3].set_weights(
[np.array([[ 1.0, 0.0, 0.0, 0.0],
[ 1.0, 0.0, 0.0, 0.0],
[ 0.0, 1.0, 0.0, 0.0],
[ 0.0, 1.0, 0.0, 0.0],
[ 0.0, 0.0, 1.0, 0.0],
[ 0.0, 0.0, 1.0, 0.0],
[ 0.0, 0.0, 0.0, 1.0],
[ 0.0, 0.0, 0.0, 1.0]],
dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])
model4.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.Adagrad(),
metrics=['accuracy'])for layer in model4.layers:
print(layer.get_weights())[array([[ 1., 0., 1., 0.],
[ 0., 1., 0., 1.],
[ 1., 0., -1., 0.],
[ 0., 1., 0., -1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
[array([[ 1., -1., 0., 0.],
[ 1., 1., 0., 0.],
[ 0., 0., 1., -1.],
[ 0., 0., -1., -1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
[array([[ 1., -1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 1., -1., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 1., -1., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 1., -1.]], dtype=float32), array([0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)]
[array([[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
model4.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])array([[0.17831734, 0.17831734, 0.17831734, 0.465048 ]], dtype=float32)
score = model4.evaluate(x4_test, y4_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))Test loss: 0.7656148672103882 Test accuracy: 1.0
model5 = keras.Sequential()
model5.add(Dense(4, activation='tanh', input_shape=(4,)))
model5.add(Dense(4, activation='tanh'))
model5.add(Dense(8, activation='relu'))
model5.add(Dense(num_classes, activation='softmax'))
model5.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.RMSprop(),
metrics=['accuracy'])
model5.summary()Model: "sequential_25" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_75 (Dense) (None, 4) 20 _________________________________________________________________ dense_76 (Dense) (None, 4) 20 _________________________________________________________________ dense_77 (Dense) (None, 8) 40 _________________________________________________________________ dense_78 (Dense) (None, 4) 36 ================================================================= Total params: 116 Trainable params: 116 Non-trainable params: 0 _________________________________________________________________
model5.fit(x4_train, y4_train, epochs=8, validation_data=(x4_test, y4_test))Epoch 1/8 125/125 [==============================] - 0s 3ms/step - loss: 1.3126 - accuracy: 0.3840 - val_loss: 1.1926 - val_accuracy: 0.6110 Epoch 2/8 125/125 [==============================] - 0s 2ms/step - loss: 1.0978 - accuracy: 0.5980 - val_loss: 1.0085 - val_accuracy: 0.6150 Epoch 3/8 125/125 [==============================] - 0s 2ms/step - loss: 0.9243 - accuracy: 0.7035 - val_loss: 0.8416 - val_accuracy: 0.7380 Epoch 4/8 125/125 [==============================] - 0s 2ms/step - loss: 0.7522 - accuracy: 0.8740 - val_loss: 0.6738 - val_accuracy: 1.0000 Epoch 5/8 125/125 [==============================] - 0s 2ms/step - loss: 0.5811 - accuracy: 1.0000 - val_loss: 0.5030 - val_accuracy: 1.0000 Epoch 6/8 125/125 [==============================] - 0s 2ms/step - loss: 0.4134 - accuracy: 1.0000 - val_loss: 0.3428 - val_accuracy: 1.0000 Epoch 7/8 125/125 [==============================] - 0s 2ms/step - loss: 0.2713 - accuracy: 1.0000 - val_loss: 0.2161 - val_accuracy: 1.0000 Epoch 8/8 125/125 [==============================] - 0s 1ms/step - loss: 0.1621 - accuracy: 1.0000 - val_loss: 0.1225 - val_accuracy: 1.0000
<tensorflow.python.keras.callbacks.History at 0x1ed00809700>
model5.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])array([[3.2040708e-02, 1.0065207e-03, 4.9596769e-04, 9.6645677e-01]],
dtype=float32)score = model5.evaluate(x4_test, y4_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))Test loss: 0.1224619448184967 Test accuracy: 1.0
import contextlib
@contextlib.contextmanager
def printoptions(*args, **kwargs):
original = np.get_printoptions()
np.set_printoptions(*args, **kwargs)
try:
yield
finally:
np.set_printoptions(**original)with printoptions(precision=1, suppress=True):
for layer in model5.layers:
print(layer.get_weights())[array([[ 0.7, 0.2, -0.7, 0.7],
[-0.5, 0.9, 0.6, 0.6],
[ 1.1, 0.2, 0.1, 0.2],
[ 0.7, 0.1, 0.3, -0.7]], dtype=float32), array([ 0. , 0.1, -0.1, -0.2], dtype=float32)]
[array([[ 0.7, 0.5, -1.1, -1.2],
[ 0.7, 0.9, -0.6, 0.3],
[ 0.1, 1.4, -0.6, 0.8],
[ 1.5, 0.1, -0.1, 0.9]], dtype=float32), array([-0.4, 0.2, -0. , 0.2], dtype=float32)]
[array([[-1. , 1. , -0.7, -0.3, 0.2, 1.3, -0.7, 0.9],
[-0.9, 0.5, 0.8, -1.3, -1.2, 1.3, 0.4, -1. ],
[ 0.9, 0.2, 0.3, 0.4, 1.3, -0.9, -0.1, -0.2],
[-0.4, 0.5, 1.1, -0.6, 1.1, 0.1, -1.5, -1. ]], dtype=float32), array([-0.1, 0.1, 0.1, 0.1, 0.2, -0. , 0.1, 0.2], dtype=float32)]
[array([[ 0.7, -0.5, 0.8, -0.5],
[-0.3, -1.6, -0.2, 0.1],
[-1.5, 0.9, 0.1, -0.5],
[ 0.6, 0.7, 1. , -1.4],
[ 0.7, -1.2, -1.6, 1.2],
[ 1. , -1.2, 0.3, -1.5],
[-0.2, 0. , 0.6, 1.3],
[-0.8, 0.2, -0.6, -1. ]], dtype=float32), array([-0.6, 0.5, -0.3, 0.4], dtype=float32)]