44 KiB
Uczenie maszynowe
5. Rekurencyjne sieci neuronowe (RNN), splotowe sieci neuronowe (CNN)
5.1. Rekurencyjne sieci neuronowe (_Recurrent Neural Networks – RNN)
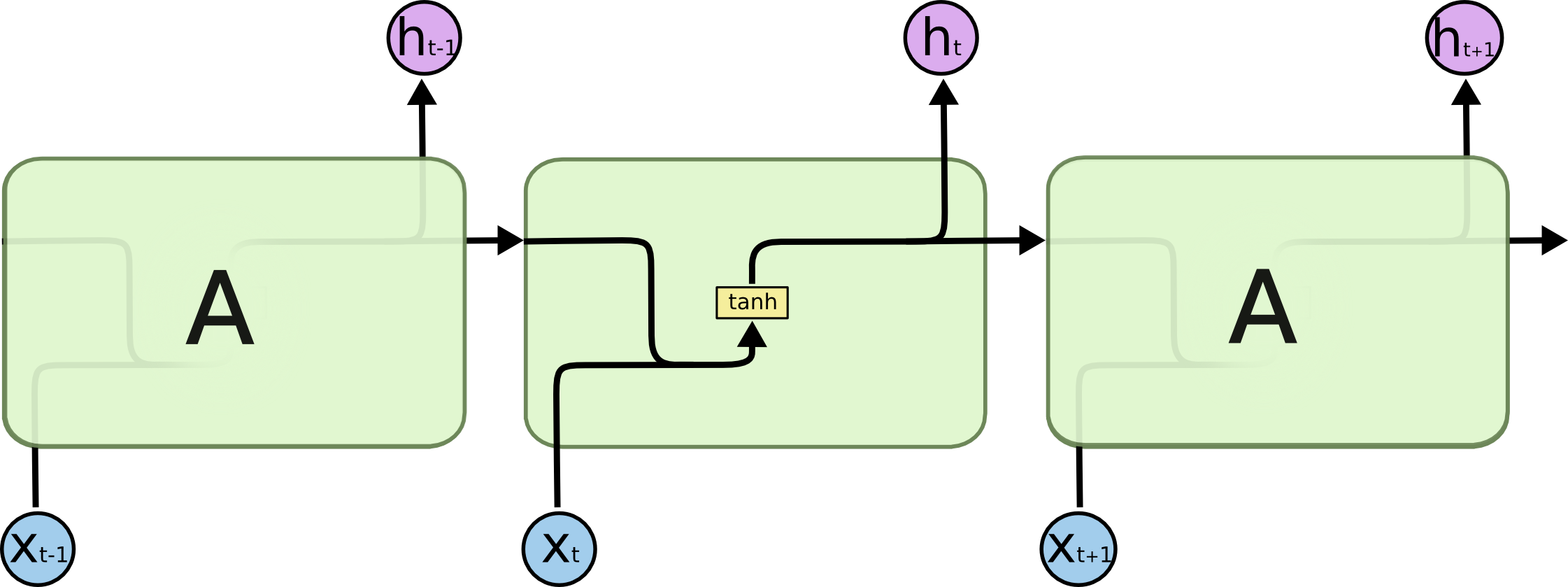
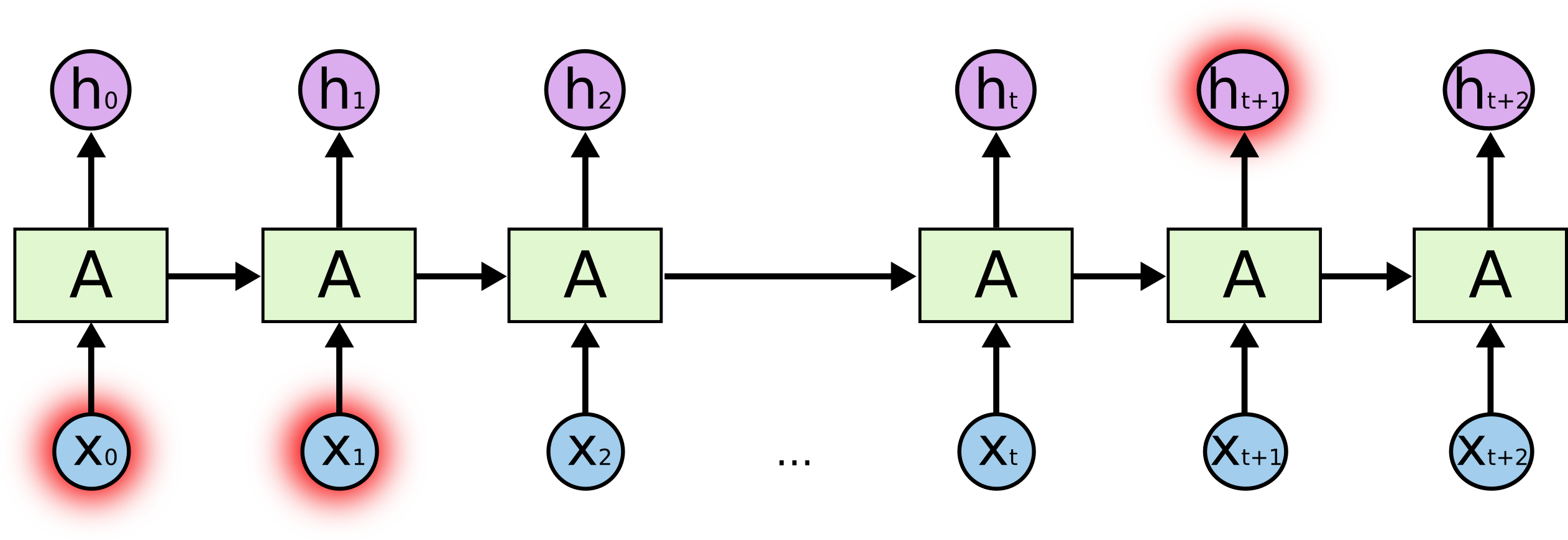
Rekurencyjna sieć neuronowa – schemat

Rekurencyjna sieć neuronowa – schemat
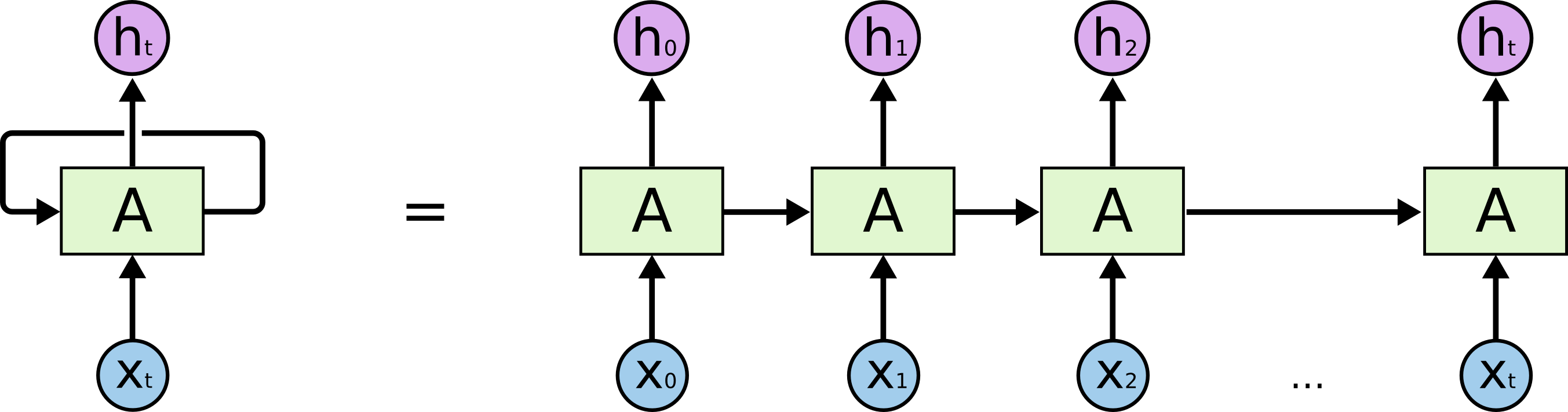
Zależności długodystansowe (_long-distance dependencies) w sieciach rekurencyjnych
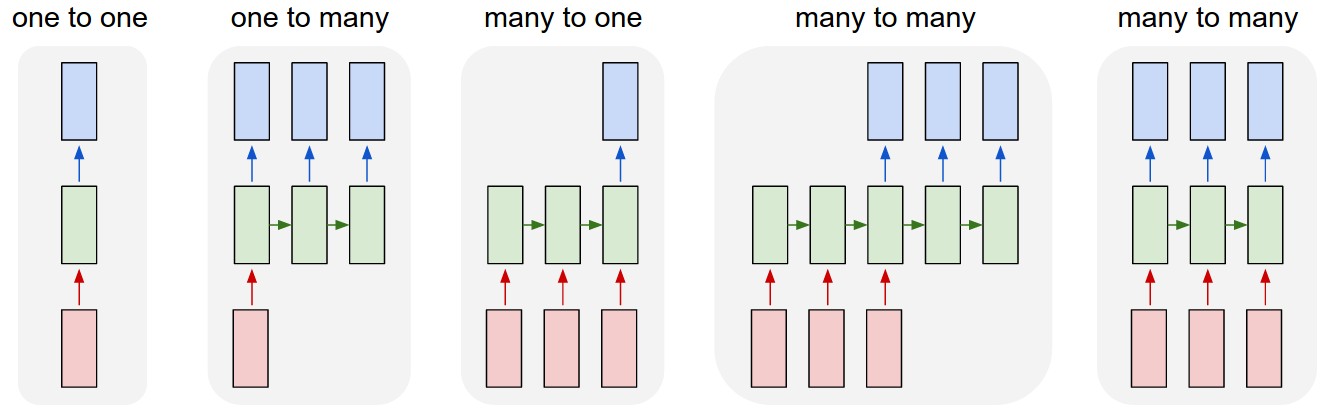
RNN – typy sekwencji
- Rekurencyjne sieci neuronowe znajduja zastosowanie w przetwarzaniu sekwencji, np. szeregów czasowych i tekstów.
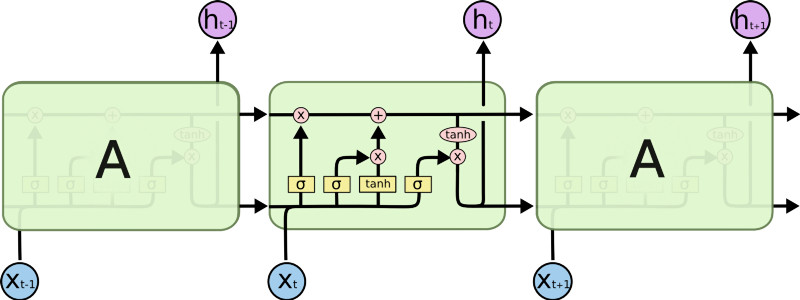
- LSTM są rozwinięciem RNN, umożliwiają „zapamiętywanie” i „zapominanie”.
Co potrafią generować rekurencyjne sieci neuronowe?
Przewidywanie ciągów czasowych za pomocą LSTM – przykład
https://machinelearningmastery.com/time-series-forecasting-long-short-term-memory-network-python/
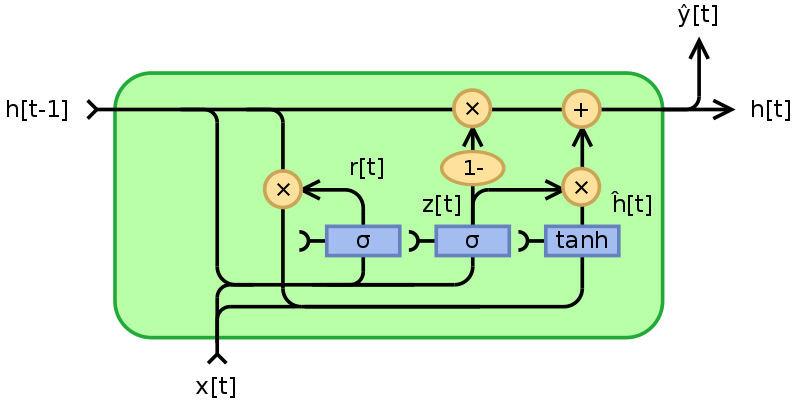
GRU – _Gated Recurrent Unit
- Rodzaj rekurencyjnej sieci neuronowej wprwadzony w 2014 roku
- Ma prostszą budowę niż LSTM (2 bramki zamiast 3).
GRU vs LSTM
LSTM – 3 bramki: wejścia (_input), wyjścia (output) i zapomnienia (forget); GRU – 2 bramki: resetu (reset) i aktualizacji (update). Bramka resetu pełni podwójną funkcję: zastępuje bramki wyjścia i zapomnienia.
GRU vs LSTM
- GRU i LSTM mają podobną skuteczność, ale GRU dzięki prostszej budowie bywa bardziej wydajna.
- LSTM sprawdza się lepiej w przetwarzaniu tekstu, ponieważ lepiej zapamiętuje zależności długosystansowe.
5.2. Splotowe sieci neuronowe (_Convolutional Neural Networks – CNN)
Splotowe (konwolucyjne) sieci neuronowe wykorzystuje się do:
- rozpoznawania obrazu
- analizy wideo
- innych zagadnień o podobnej strukturze
Innymi słowy, CNN przydają się, gdy mamy bardzo dużo danych wejściowych, w których istotne jest ich sąsiedztwo.
Przykład
Dla uproszczenia przyjmijmy, że mamy dane w postaci jendowymiarowej – np. chcemy stwierdzić, czy na danym nagraniu obecny jest głos człowieka.
Tak wygląda nasze nagranie:

(ciąg próbek dźwiękowych – możemy traktować je jak jednowymiarowe „piksele”)
Najprostsza metoda – „zwykła” jednowarstwowa sieć neuronowa (każdy z każdym):
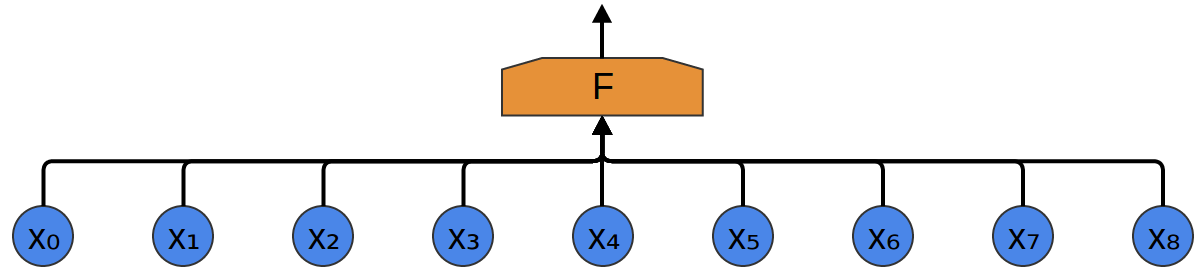
Wady:
- dużo danych wejściowych
- nie wykrywa własności „lokalnych” wejścia
Chcielibyśmy wykrywać pewne lokalne „wzory” w danych wejściowych.
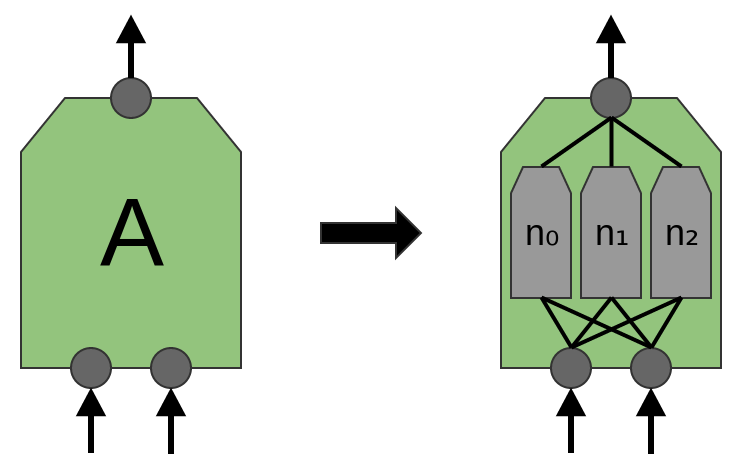
W tym celu tworzymy mniejszą sieć neuronową (mniej neuronów wejściowych) i _kopiujemy ją tak, żeby każda jej kopia działała na pewnym fragmencie wejścia (fragmenty mogą nachodzić na siebie):
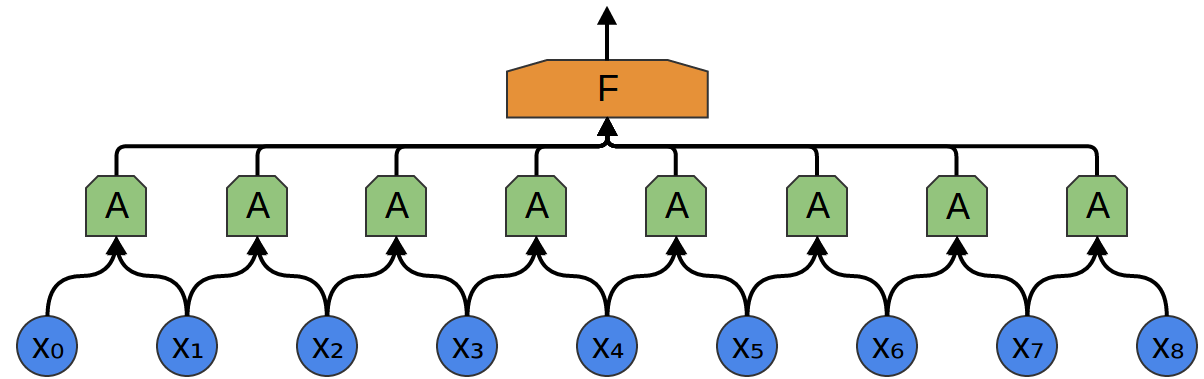
Każda z sieci A ma 2 neurony wejściowe (mało realistycznie).
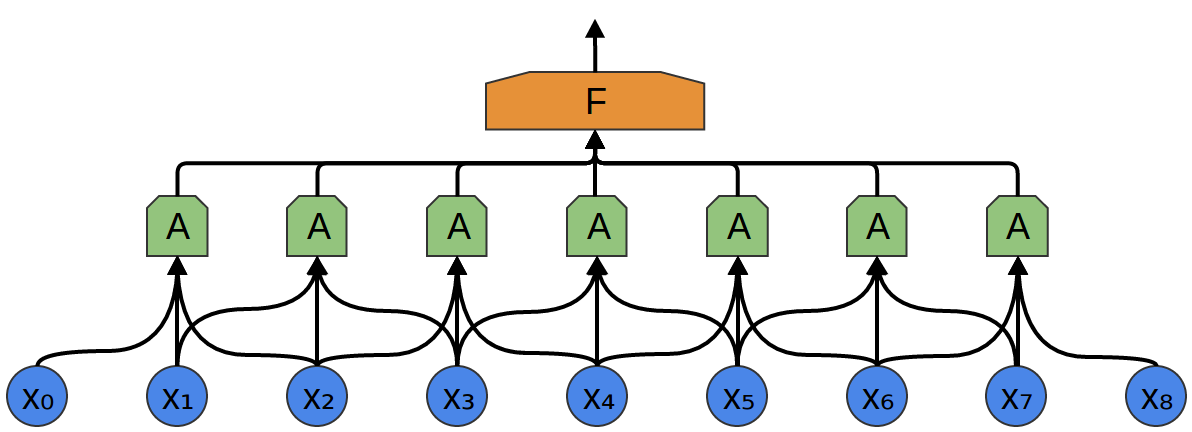
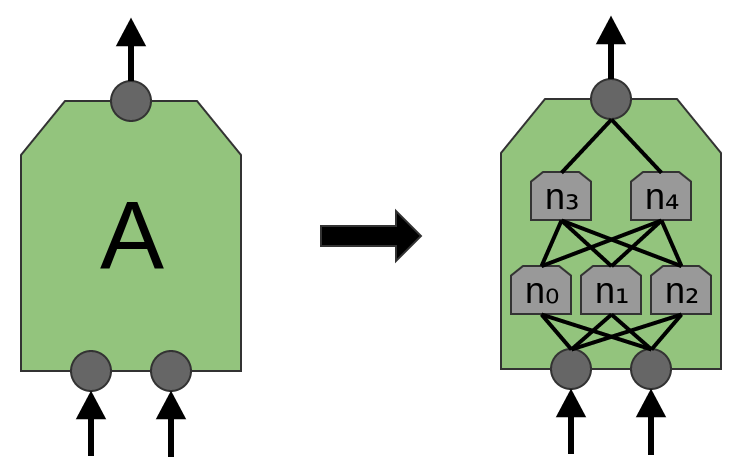
Każda z sieci A ma 3 neurony wejściowe (wciąż mało realistycznie, ale już trochę bardziej).
Warstwę sieci A nazywamy warstwą splotową (konwolucyjną).
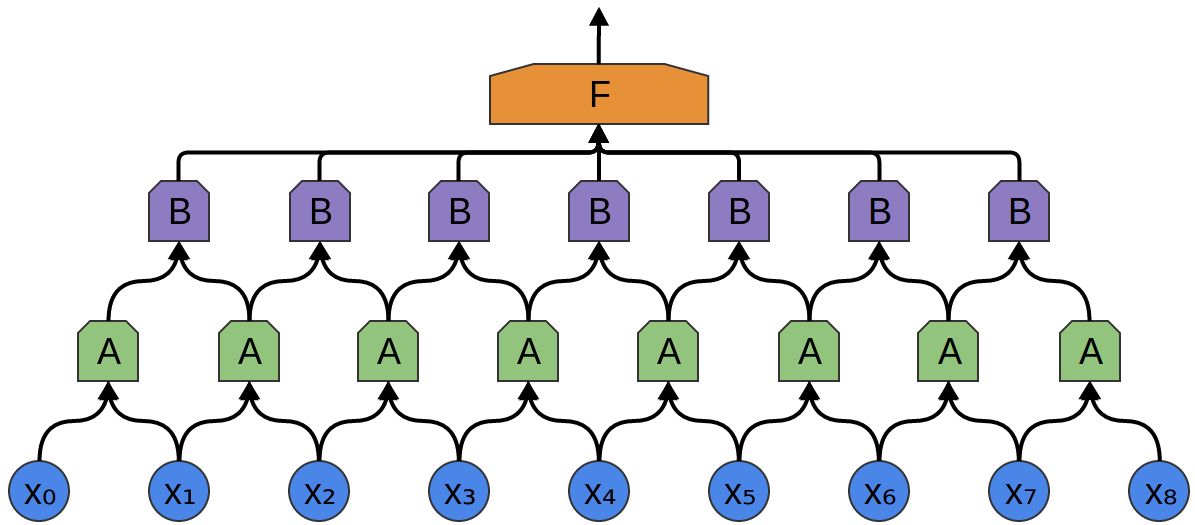
Warstw splotowych może być więcej niż jedna:
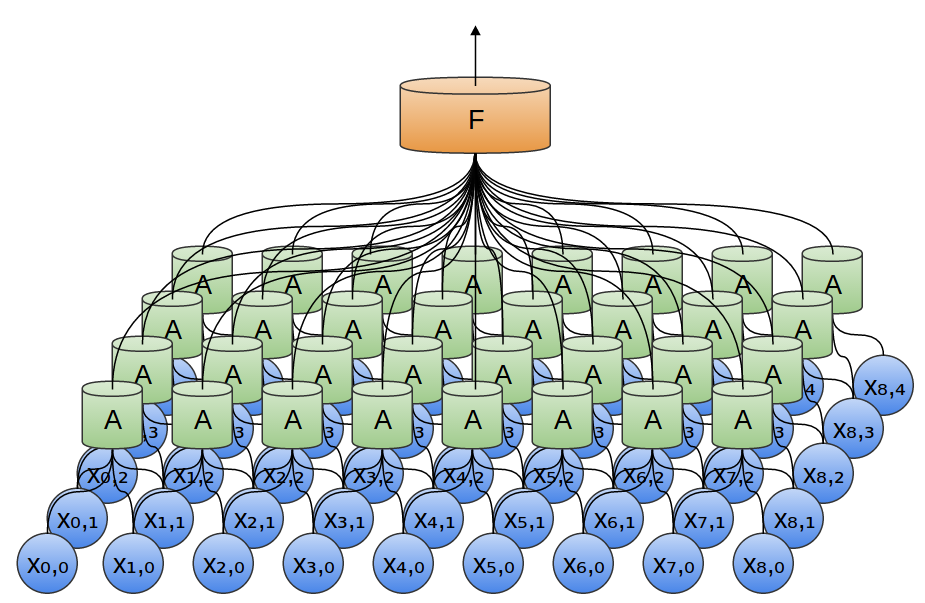
W dwóch wymiarach wygląda to tak:
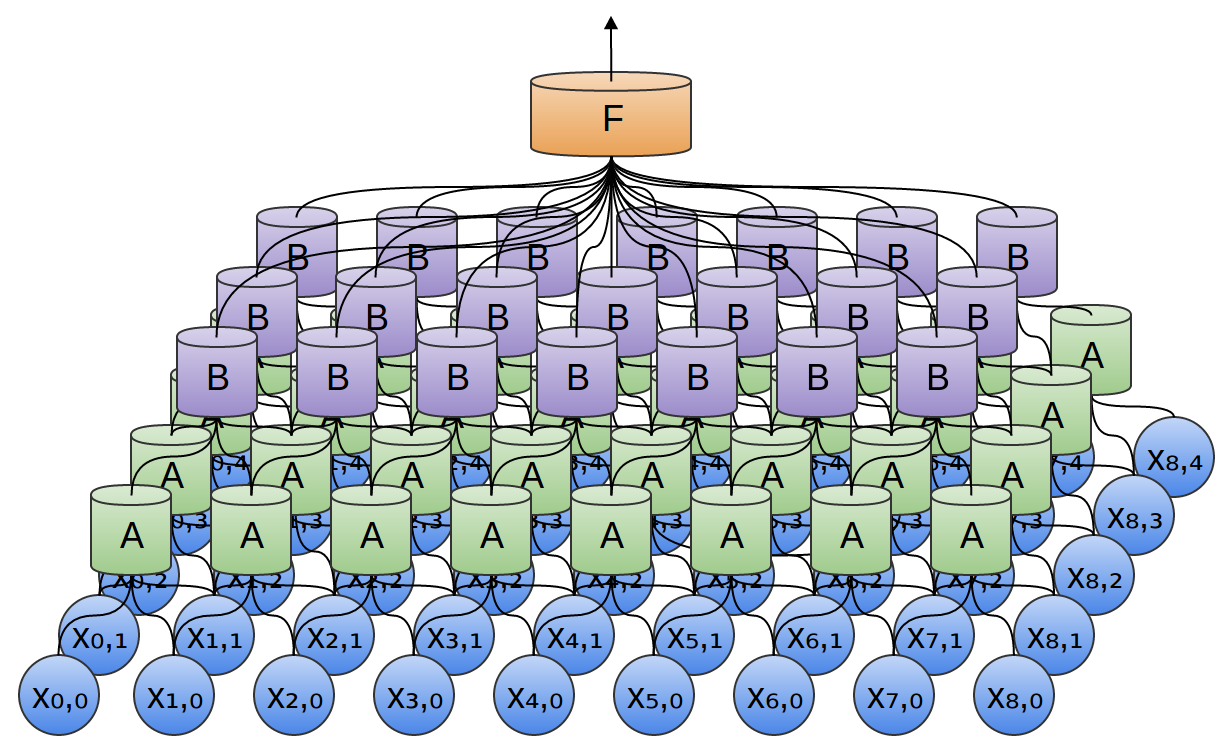
Zblizenie na pojedynczą jednostkę A:
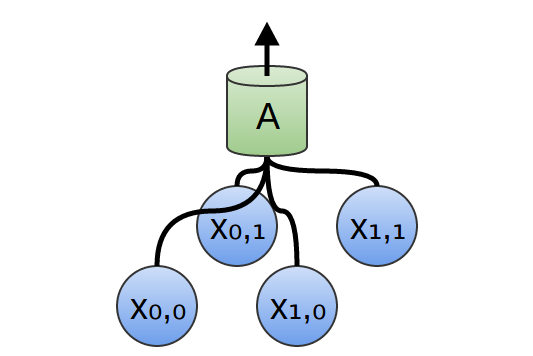
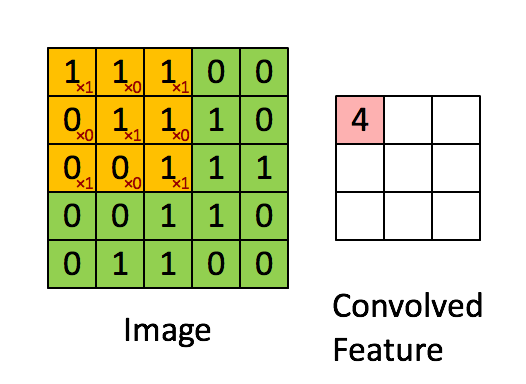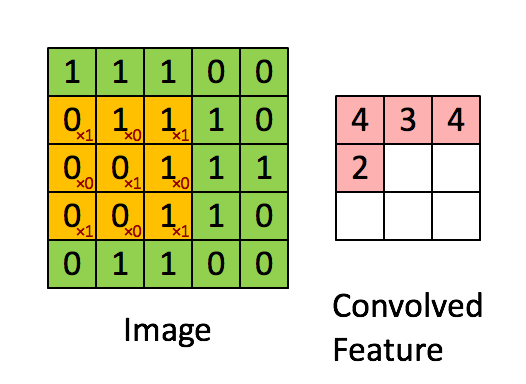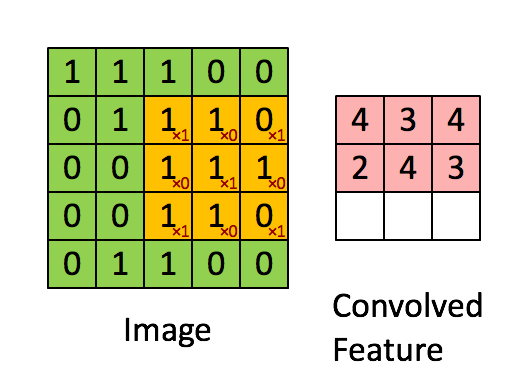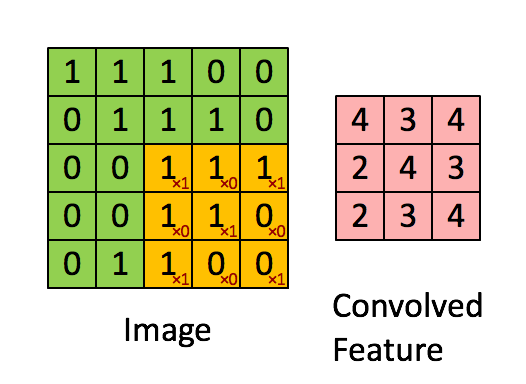
Tak definiujemy formalnie funckję splotu dla 2 wymiarów:
$$ \left[\begin{array}{ccc} a & b & c\\ d & e & f\\ g & h & i\\ \end{array}\right] * \left[\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{array}\right] =\\ (1 \cdot a)+(2 \cdot b)+(3 \cdot c)+(4 \cdot d)+(5 \cdot e)\\+(6 \cdot f)+(7 \cdot g)+(8 \cdot h)+(9 \cdot i) $$
Więcej: https://en.wikipedia.org/wiki/Kernel_(image_processing)
A tak to mniej więcej działa:
Jednostka warstwy konwolucyjnej może się składać z jednej lub kilku warstw neuronów:
Jeden neuron może odpowiadać np. za wykrywanie pionowych krawędzi, drugi poziomych, a jeszcze inny np. krzyżujących się linii.
Przykładowe filtry, których może nauczyć się pierwsza warstwa konwolucyjna:

_Pooling
Obrazy składają się na ogół z milionów pikseli. Oznacza to, że nawet po zastosowaniu kilku warstw konwolucyjnych mielibyśmy sporo parametrów do wytrenowania.
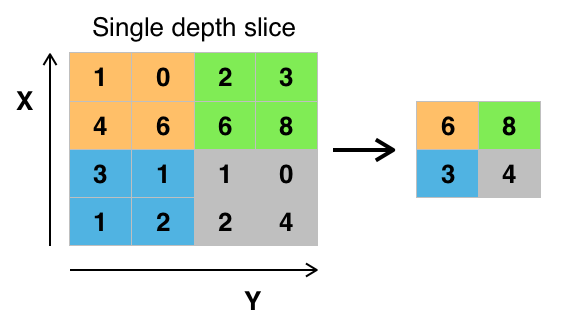
Żeby zredukować liczbę parametrów, a dzięki temu uprościć obliczenia, stosuje się warstwy _pooling.
_Pooling to rodzaj próbkowania. Najpopularniejszą jego odmianą jest max-pooling, czyli wybieranie najwyższej wartości spośród kilku sąsiadujących pikseli.
Warstwy _pooling i konwolucyjne można przeplatać ze sobą:
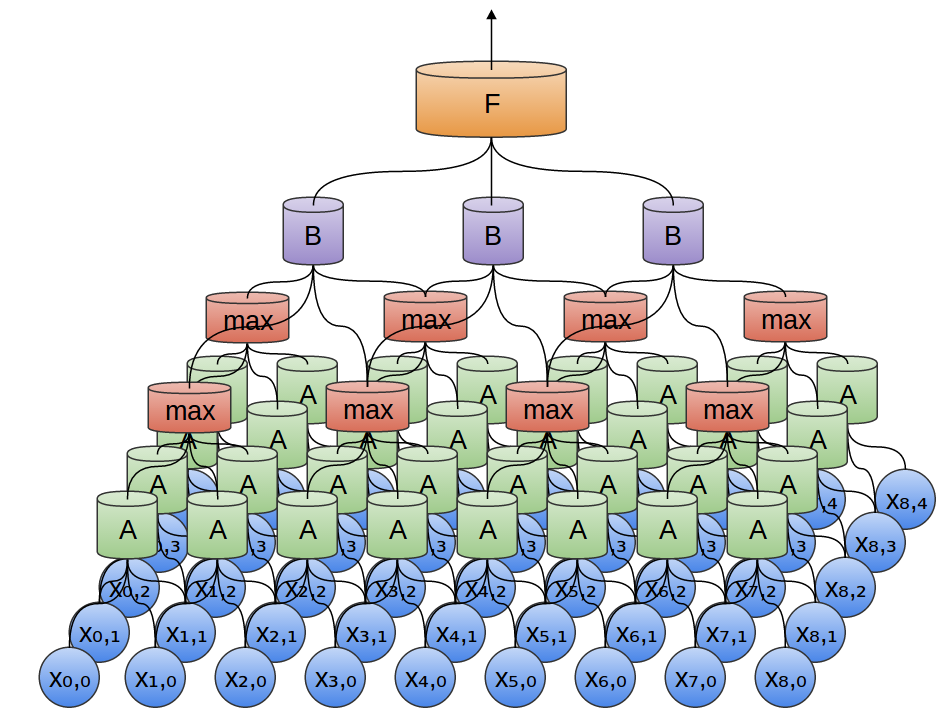
_Pooling – idea: nie jest istotne, w którym dokładnie miejscu na obrazku dana cecha (krawędź, oko, itp.) się znajduje, wystarczy przybliżona lokalizacja.
Do sieci konwolucujnych możemy dokładać też warstwy ReLU.
Możliwości konwolucyjnych sieci neuronowych

Przykład: MNIST
%matplotlib inline
import math
import matplotlib.pyplot as plt
import numpy as np
import random
from IPython.display import YouTubeVideo# źródło: https://github.com/keras-team/keras/examples/minst_mlp.py
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
# załaduj dane i podziel je na zbiory uczący i testowy
(x_train, y_train), (x_test, y_test) = mnist.load_data()def draw_examples(examples, captions=None):
plt.figure(figsize=(16, 4))
m = len(examples)
for i, example in enumerate(examples):
plt.subplot(100 + m * 10 + i + 1)
plt.imshow(example, cmap=plt.get_cmap('gray'))
plt.show()
if captions is not None:
print(6 * ' ' + (10 * ' ').join(str(captions[i]) for i in range(m)))draw_examples(x_train[:7], captions=y_train)5 0 4 1 9 2 1
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28if keras.backend.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape: {}'.format(x_train.shape))
print('{} train samples'.format(x_train.shape[0]))
print('{} test samples'.format(x_test.shape[0]))
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)x_train shape: (60000, 28, 28, 1) 60000 train samples 10000 test samples
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))Train on 60000 samples, validate on 10000 samples Epoch 1/12 60000/60000 [==============================] - 333s - loss: 0.3256 - acc: 0.9037 - val_loss: 0.0721 - val_acc: 0.9780 Epoch 2/12 60000/60000 [==============================] - 342s - loss: 0.1088 - acc: 0.9683 - val_loss: 0.0501 - val_acc: 0.9835 Epoch 3/12 60000/60000 [==============================] - 366s - loss: 0.0837 - acc: 0.9748 - val_loss: 0.0429 - val_acc: 0.9860 Epoch 4/12 60000/60000 [==============================] - 311s - loss: 0.0694 - acc: 0.9788 - val_loss: 0.0380 - val_acc: 0.9878 Epoch 5/12 60000/60000 [==============================] - 325s - loss: 0.0626 - acc: 0.9815 - val_loss: 0.0334 - val_acc: 0.9886 Epoch 6/12 60000/60000 [==============================] - 262s - loss: 0.0552 - acc: 0.9835 - val_loss: 0.0331 - val_acc: 0.9890 Epoch 7/12 60000/60000 [==============================] - 218s - loss: 0.0494 - acc: 0.9852 - val_loss: 0.0291 - val_acc: 0.9903 Epoch 8/12 60000/60000 [==============================] - 218s - loss: 0.0461 - acc: 0.9859 - val_loss: 0.0294 - val_acc: 0.9902 Epoch 9/12 60000/60000 [==============================] - 219s - loss: 0.0423 - acc: 0.9869 - val_loss: 0.0287 - val_acc: 0.9907 Epoch 10/12 60000/60000 [==============================] - 218s - loss: 0.0418 - acc: 0.9875 - val_loss: 0.0299 - val_acc: 0.9906 Epoch 11/12 60000/60000 [==============================] - 218s - loss: 0.0388 - acc: 0.9879 - val_loss: 0.0304 - val_acc: 0.9905 Epoch 12/12 60000/60000 [==============================] - 218s - loss: 0.0366 - acc: 0.9889 - val_loss: 0.0275 - val_acc: 0.9910
<keras.callbacks.History at 0x7f70b80b1a10>
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])('Test loss:', 0.027530849870144449)
('Test accuracy:', 0.99099999999999999)
5.3. Autoencoder
- Uczenie nienadzorowane
- Dane: zbiór nieanotowanych przykładów uczących $\{ x^{(1)}, x^{(2)}, x^{(3)}, \ldots \}$, $x^{(i)} \in \mathbb{R}^{n}$
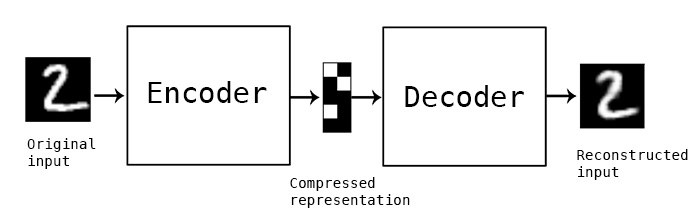
Autoencoder (encoder-decoder)
Sieć neuronowa taka, że:
- warstwa wejściowa ma $n$ neuronów
- warstwa wyjściowa ma $n$ neuronów
- warstwa środkowa ma $k < n$ neuronów
- $y^{(i)} = x^{(i)}$ dla każdego $i$
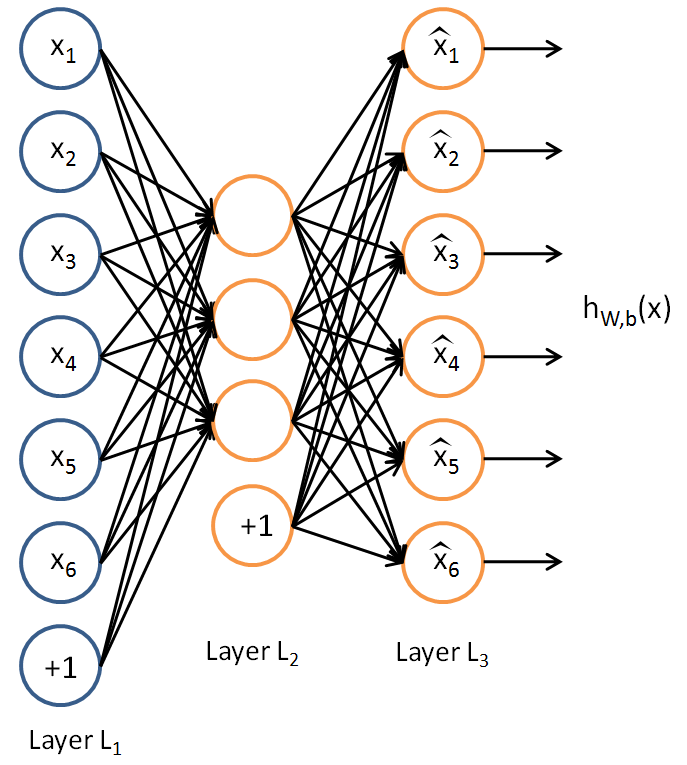
Co otrzymujemy dzięki takiej sieci?
- $y^{(i)} = x^{(i)} ; \Longrightarrow ;$ Autoencoder próbuje nauczyć się funkcji $h(x) \approx x$, czyli funkcji identycznościowej.
- Warstwy środkowe mają mniej neuronów niż warstwy zewnętrzne, więc żeby to osiągnąć, sieć musi znaleźć bardziej kompaktową (tu: $k$-wymiarową) reprezentację informacji zawartej w wektorach $x_{(i)}$.
- Otrzymujemy metodę kompresji danych.
Innymi słowy:
- Ograniczenia nałożone na reprezentację danych w warstwie ukrytej pozwala na „odkrycie” pewnej struktury w danych.
- _Decoder musi odtworzyć do pierwotnej postaci reprezentację danych skompresowaną przez encoder.
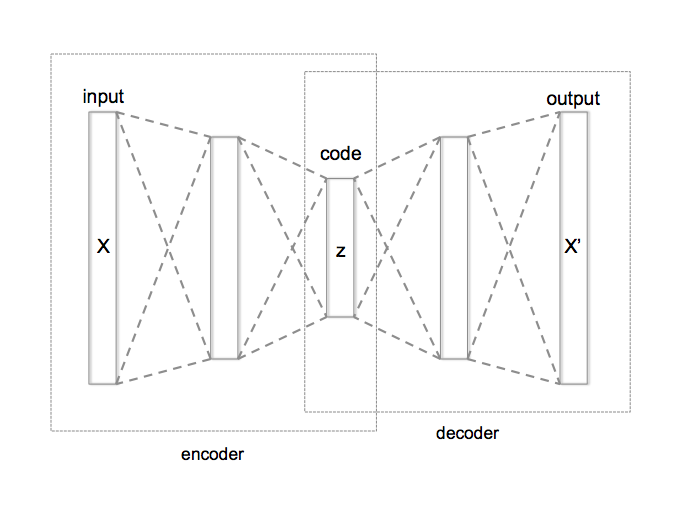
- Całkowita liczba warstw w sieci autoencodera może być większa niż 3.
- Jako funkcji kosztu na ogół używa się błędu średniokwadratowego (_mean squared error, MSE) lub entropii krzyżowej (binary crossentropy).
- Autoencoder może wykryć ciekawe struktury w danych nawet jeżeli $k \geq n$, jeżeli na sieć nałoży się inne ograniczenia.
- W wyniku działania autoencodera uzyskujemy na ogół kompresję stratną.
Autoencoder a PCA
Widzimy, że autoencoder można wykorzystać do redukcji liczby wymiarów. Podobną rolę pełni poznany na jednym z poprzednich wykładów algorytm PCA (analiza głównych składowych, _principal component analysis).
Faktycznie, jeżeli zastosujemy autoencoder z liniowymi funkcjami aktywacji i pojedynczą sigmoidalną warstwą ukrytą, to na podstawie uzyskanych wag można odtworzyć główne składowe używając rozkładu według wartości osobliwych (_singular value decomposition, SVD).
Autoencoder odszumiający
Jeżeli na wejściu zamiast „czystych” danych użyjemy danych zaszumionych, to otrzymamy sieć, która może usuwać szum z danych:
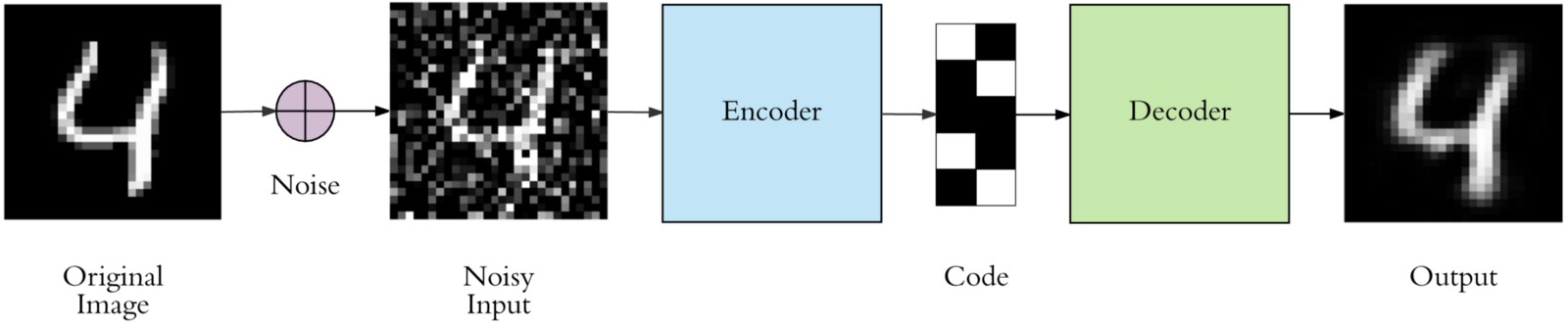
Autoencoder – zastosowania
Autoencoder sprawdza się gorzej niż inne algorytmy kompresji, więc nie stosuje się go raczej jako metody kompresji danych, ale ma inne zastosowania:
- odszumianie danych
- redukcja wymiarowości
- VAE (_variational autoencoders) – http://kvfrans.com/variational-autoencoders-explained/
5.4. Word embeddings
_Word embeddings – sposoby reprezentacji słów jako wektorów liczbowych
Znaczenie wyrazu jest reprezentowane przez sąsiednie wyrazy:
“A word is characterized by the company it keeps.” (John R. Firth, 1957)
- Pomysł pojawił sie jeszcze w latach 60. XX w.
- _Word embeddings można uzyskiwać na różne sposoby, ale dopiero w ostatnim dziesięcioleciu stało się opłacalne użycie w tym celu sieci neuronowych.
Przykład – 2 zdania:
- "have a good day"
- "have a great day"
Słownik:
- {"a", "day", "good", "great", "have"}
- Aby wykorzystać metody uczenia maszynowego do analizy danych tekstowych, musimy je jakoś reprezentować jako liczby.
- Najprostsza metoda to wektory jednostkowe:
- "a" = $(1, 0, 0, 0, 0)$
- "day" = $(0, 1, 0, 0, 0)$
- "good" = $(0, 0, 1, 0, 0)$
- "great" = $(0, 0, 0, 1, 0)$
- "have" = $(0, 0, 0, 0, 1)$
- Taka metoda nie uwzględnia jednak podobieństw i różnic między znaczeniami wyrazów.
Metody uzyskiwania _word embeddings:
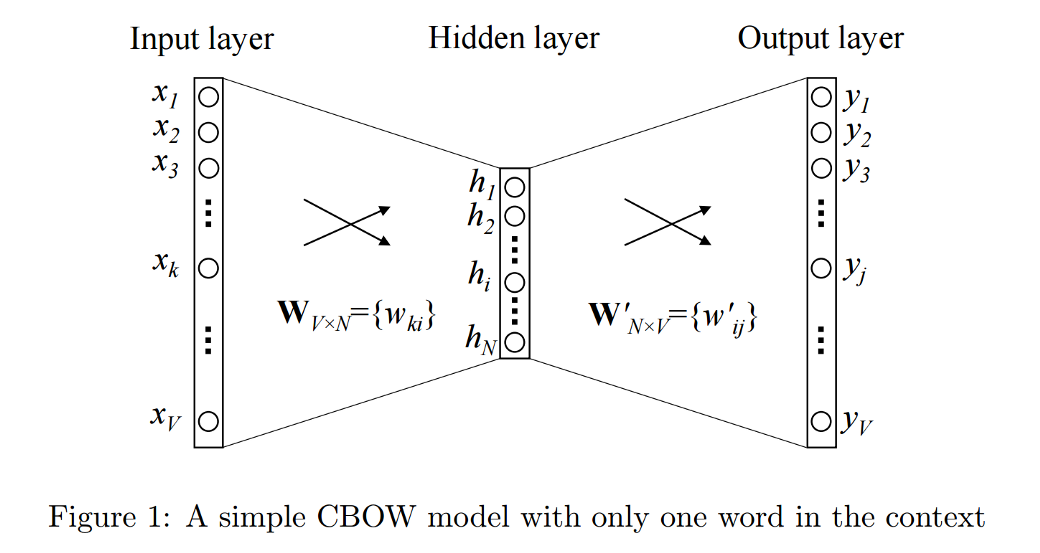
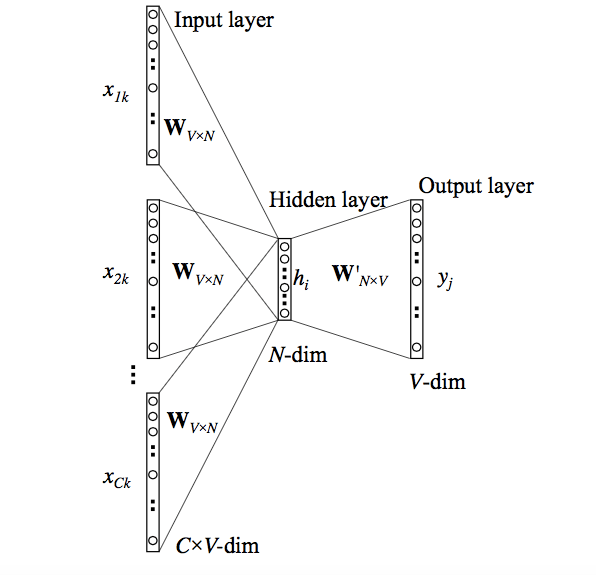
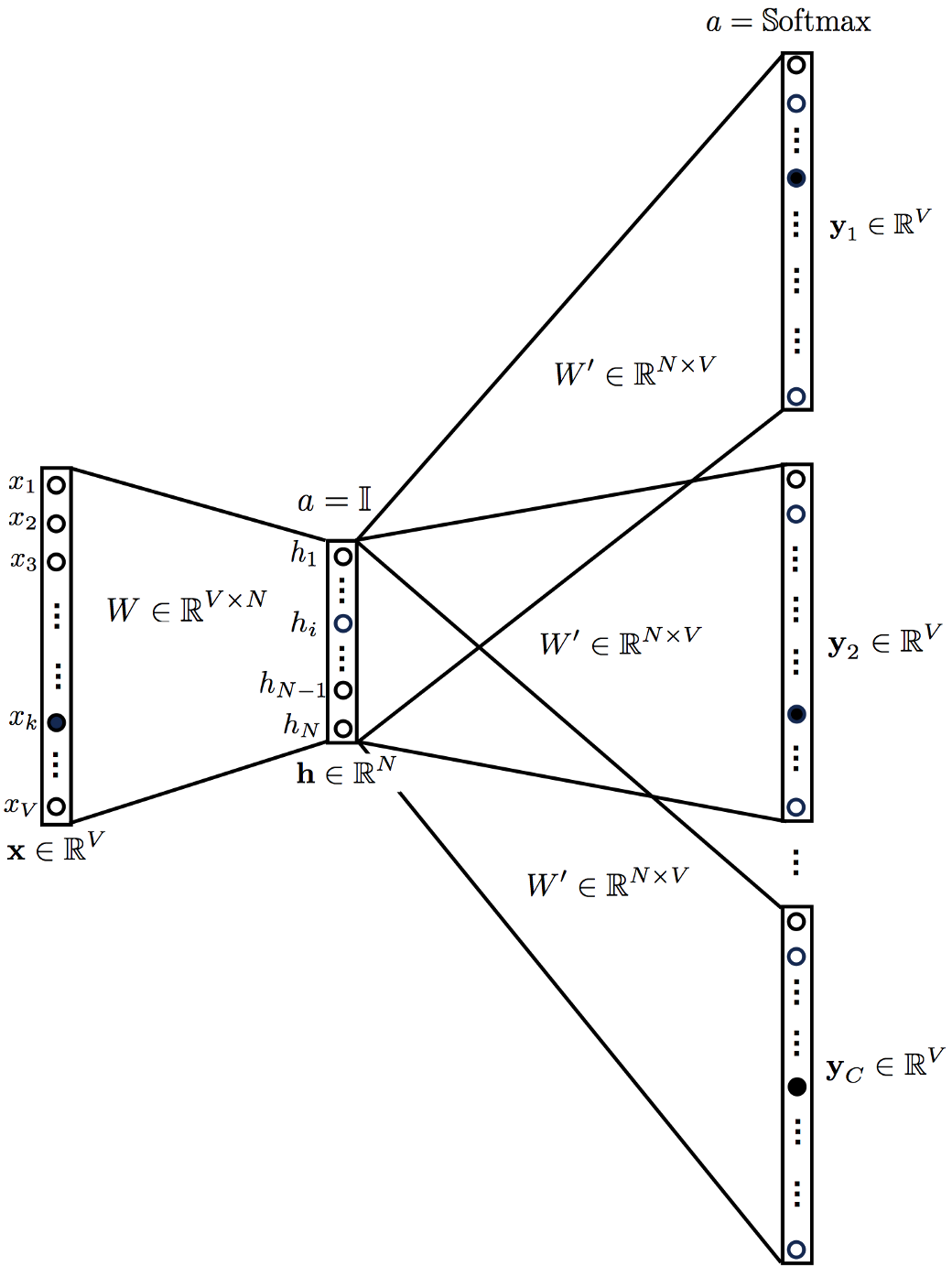
- Common Bag of Words (CBOW)
- Skip Gram
Obie opierają się na odpowiednim użyciu autoencodera.
Skip Gram a CBOW
- Skip Gram lepiej reprezentuje rzadkie wyrazy i lepiej działa, jeżeli mamy mało danych.
- CBOW jest szybszy i lepiej reprezentuje częste wyrazy.
Popularne modele _word embeddings
- Word2Vec (Google)
- GloVe (Stanford)
- FastText (Facebook)
5.5. Tłumaczenie neuronowe
_Neural Machine Translation (NMT)
Neuronowe tłumaczenie maszynowe również opiera się na modelu _encoder-decoder:
- _Encoder koduje z języka źródłowego na abstrakcyjną reprezentację.
- _Decoder odkodowuje z abstrakcyjnej reprezentacji na język docelowy.