MWS/cw1 p2/cw1.md

L-System

W tej części zajęć skupimy się na tworzeniu L-Systemów i wykorzystaniu ich do reprezentacji zjawisk przyrodniczych.

Przypomnienie L-System to system przepisywania i gramatyka formalna. Składa się z: symboli, które tworzą ciągi znaków; reguł produkcyjnych, które opisują na co należy przepisać dany znak; aksjomatu, czyli początkowego ciągu znaków; i mechanizmu, który tłumaczy ciąg znaków na reprezentacje geometryczną

Bazą dla tych zajęć jest książka Algorithmic Beauty of Plants dostępna za darmo pod linkiem lub w wyższej jakości

Składnia L-Systemów

Projekt zawiera bibliotekę, która interpretuje L-Systemy. Ich definicję pobiera z oddzielnego pliku. Ich składnie opisuję definicja L-Systemu opisującego rozwój bakterii Anabaena znajduje się w projekcie pod ścieżką Assets\LSystem\Anabaena.txt i wygląda następująco:

#axiom
L
#rules
L->lR
R->Lr
l->L
r->R
#end rules

Plik należy zacząć od linii #axiom, następnie w następnej linii zamieścić ciąg początkowy. Później pomiędzy liniami #rules i #end rules umieścić instrukcje przepisywania według zasady: <znak przepisywany>-><wynik przepisania> każdy znak przed strzałką i po strzałce (z wyjątkiem reguł o których później) jest traktowany jako następny symbol. W przypadku kilku reguł, które dotyczą tego samego symbolu wykona się ta, która jest wyżej w pliku. Między reguły można dodawać komentarze, znakiem komentującym jest #. Jeżeli znak nie posiada żadnej reguły, która by go opisywała, to nie jest on zmieniany.

Odpal scenę LSystemFromFile, zaznacz LSystemController w panelu po prawej. Po lewej w polu L System Path wpisz Assets\LSystem\Anabaena.txt kliknij Load File, by załadować LSystem. Następnie Evaluate, by wykonać przepisanie. W scenie wyświetlą się obiekty reprezentujące symbole a w konsoli wyświetli się wynik przepisania.

Składnia wszystkich rozszerzeń jest zaprezentowana w pliku SampleLSystem.txt w tej chwili niektóre reguły mogą byc niezrozumiałe, ale może się on przydać później jako wzorzec.

Turtle Graphics

Turtle Graphics jest metodą tworzenia grafiki komputerowej, wykorzystuje kursor (tytułowego żółwia) wykonujący instrukcje w przestrzeni lokalnej.

L-Systemy można interpretować za pomocą Turtle Graphics, poprzez przypisanie każdemu symbolowi instrukcji jaką ma wykonać żółw. Następnie żółw będzie wykonywał kolejne instrukcje czytając napis od lewej do prawej.

Na początek zaczniemy od prostej reprezentacji, gdzie + będzie oznaczał w kierunku zgodnym z ruchem wskazówek zegara o wskazany kąt, natomiast - w przeciwnym. Kąt zwyczajowo oznacza się grecką literą \delta. Każdy inny symbol będzie oznaczał idź prosto o 1.

Odpal Scenę LSystem2D, załaduj plik Sierpinski.txt, ustaw kąt na 60 stopni i wykonaj kilka kroków.

Zadanie

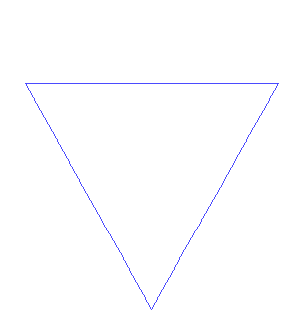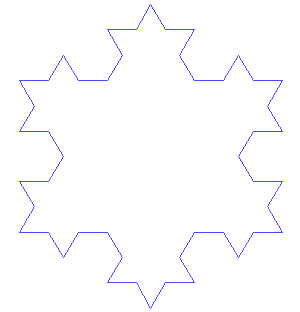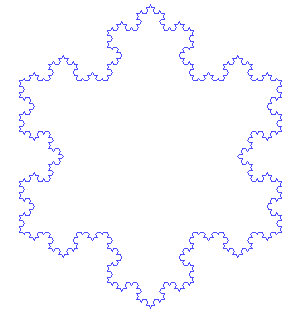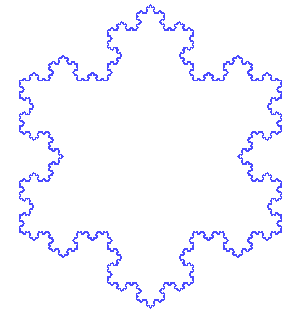
napisz Lsystem, który będzie rysował gwiazdkę kocha

1. Krzywa kocha:

Opis:

1. Podziel linię na 3 równę części
2. Przy środkowej części narysuj równoboczny trójkąt zwrócony na zewnątrz
3. Usuń środkową część pierwotnej lini

Musimy z jednej lini zrobić 4 nowe, z czego pierwsza i ostatnia idą w tym samym kierunku, a dwie środkowe idą pod innym kątem (podpowiedź: dając dwa razy + lub - możesz zwiększyć kąt)

2. W pierwszym kroku L-Systemu utwórz trójkąt

   

Bracketed L-systems

W podstawowej wersji L-Systemy są pojedyńczym ciągiem znaków, by uzyskać możliwość tworzenia rozgałęzień wprowadzamy dwa specjalne znaki [ oraz ] pierwszy mówi, żeby zapamiętać obecny stan, drugi oznacza by wrócić do stanu zapamiętanym przy ostatnim znaku [. Przykładowo ciąg symboli F[+FFF][-F]FF dla \delta=90 będzie reprezentowany następująco

Zadanie

Wyświetl poniższe L-Systemy. Zmodyfikuj definicję drugiego, by dodstać asymetryczną roślinę


Pisanie własnej interpretacji LSystemów

Wróćmy do sceny LSystemFromFile W tej scenie zamiast kresek pojawiają się figury reprezentujące komórki (czerwona lewa, zielona prawa, niska młoda, wysoka dorosła). Otwórz skrypt AnabeanaTurtle.cs, który odpowiada za rysowanie. Zawiera on klasę AnabeanaTurtle dziedziczącą po TurtleLSystem. TurtleLSystem jest klasą abstrakcyjną, wymaga zdefiniowania funkcji initLiteralInterpretation, w której należy opisać jak interpretować symbole.

    protected override void initLiteralInterpretation() {
        turtleInterpretation = new Dictionary<string, Func<float[], Tuple<GameObject, Matrix4x4>>>();
        //turtleInterpretation
        var transformation = Matrix4x4.Translate(new Vector3(0.0f, 0.1f, 0)) * Matrix4x4.Scale(new Vector3 (0.05f, 0.1f, 0.05f));

        turtleInterpretation.Add("+", (float[] args) => new Tuple<GameObject, Matrix4x4>(null, Matrix4x4.Rotate(Quaternion.Euler(0, 0, -angle))));
        turtleInterpretation.Add("-", (float[] args) => new Tuple<GameObject, Matrix4x4>(null, Matrix4x4.Rotate(Quaternion.Euler(0, 0, angle))));

        //Wildcard how to represent any other symbol
        turtleInterpretation.Add("*.*", (float[] args) => new Tuple<GameObject, Matrix4x4>(obj, transformation));
    }

Żeby tego dokonać należy uzupełnić słownik turtleInterpretation, którego kluczami są opisywane symbole jako stringi. Natomiast wartościami są funkcje, które przyjmują jako argument tablicę parametrów danego symbolu (o tym później) a zwracają Krotkę, której pierwszym elementem jest rysowany obiekt, natomiast drugim transformacja, jaką wykona żółw. Powyższym przykładzie obiekty są czytane z modeli a transformacja zawsze jest taka sama, czyli translacja o wektor (0.1,0,0) i skalowanie o wektor (0.1,0.1,0.1). (Skalowania nie są pamiętane przez żółwia)

Te funkcje są wykorzystywane przez żółwia do interpretacji ciągu symboli. Przykładowo LRr zostanie zinterpretowany następująco:

• żółw przesuwa się o 0.1 w osi X umieszcza bigL w punkcie (0.1,0,0)
• żółw przesuwa się o 0.1 w osi X umieszcza bigR w punkcie (0.2,0,0) (ponieważ (0.1,0,0)+(0.1,0,0)=(0.2,0,0) )
• żółw przesuwa się o 0.1 w osi X umieszcza bigL w punkcie (0.3,0,0)

Zadanie

Jak wyszukasz w internecie obrazki Anabaeny, zobaczysz, że są one często powykręcane, dodaj do macierz przekształceń obroty w osi Y o losowy kąt pomiędzy -20 a 20 stopni.

Parametryczne L-Systemy

Parametryczne L-Systemy operują na symbolach parametrycznych znakach, czyli takich, które posiadają 0 lub więcej parametrów rzeczywistych. Pozwala to przechowywać różne wewnętrzne stany obiektów. Przykładowo dla modelu Anabeany powyżej rozróżniamy tylko 2 stany, młody i dorosły. Dzięki parametrycznym L-Systemom możemy opisać wiek w sposób bardziej ciągły. Przykładowo poniższy L-System komórki która rośnie i jak osiągnie odpowiedni wiek rozdziela się na dwie młode komórki

#axiom 
B(1)
#rules
B(a) : a<2 -> B(a+0.1)
B(a) : a>=2 -> B(1)B(1)
#end rules

Parametry zapisuje się wewnątrz nawiasów po przecinku. W aksjomacie muszą one mieć wartości liczbowe. Po lewej stronie trzeba nadać parametrom nazwy (mogą mieć one więcej niż jeden znak). Symbole są identyfikowane po nazwie i liczbie znaków. Po dwukropku można podać warunki logiczne jakie musi spełnić symbol. można w tym umieszczać operacje matematyczne, dozwolone jest mnożenie, dzielenie, dodawanie i odejmowanie. podobnie w parametrach po prawej stronie

Zadanie

Napisz dla parametrycznej wersji Anabeny taką interpretację, żeby komórki rosły wraz z wiekiem.

Stochastyczne L-Systemy

Niektóre procesy biologiczne są zbyt skomplikowane albo niedostatecznie zbadane, żeby można je było je zasymulować lub zwyczajnie nie mamy potrzeby symulować mechanizmów tak dokładnie. Zamiast tego możemy skorzystać z losowości, która przybliży zachowanie natury.

Przykładowo możemy losowo decydować czy w roślinie wyrośnie boczna gałąź czy nie. Co realizuje poniższy L-System (znajduje się on także w pliku stochastic.txt)

#axiom
B
#rules
B -> #stochastic
p=3 FB
p=1 [+FB]FB
p=1 [-FB]FB
p=1 F
#stochastic end
#rules end

W powyższym przypadku mamy symbol B, który symbolizuje merystem (część rośliny zdolną do rozwoju); F oznacza rozwiniętą gałąź. B może rozwinąć łodygę, wytworzyć gałąź po prawej, wytworzyć gałąź po lewej lub zaprzestać rozwój.

Odpal scenę LSystem2D załaduj stochastic.txt i odpal kilka razy od początku (żeby zresetować, kliknij Load File).

Reguły stochastyczne należy zacząć od słowa #stochastic. Następnie po linijce wypisać wyniki, poprzedzając je frazą p=W, gdzie W to waga danego wyniku. Wagi mogą być dowolną dodatnią liczbą rzeczywistą. Interpreter na podstawie wag przydzieli prawdopodobieństwo kolejnym wynikom. Przykładowo w powyższym L-Systemie reguły zostaną wykonane następująco:

• FB z prawdopodobieństwem \frac{3}{6}
• [+FB]FB z prawdopodobieństwem \frac{1}{6}
• [+FB]FB z prawdopodobieństwem \frac{1}{6}
• F z prawdopodobieństwem \frac{1}{6}

zadanie

Obecnie zdarza się tak, że L-System wchodzi w ostatnią regułę na samym początku i nic nie wyrasta. Innym razem wyrasta bardzo dużo odgałęzień i całość wymyka się spod kontroli a na pewno przestaje przypominać roślinę. Pomyśl jak można zaradzić tym dwóm problemom, zmodyfikuj L-System tak, by ich uniknąć. Możesz dodać nowe symbole lub/i wykorzystać symbole parametryczne.

Zadanie domowe

Scena LSystem3D jest kopią sceny LSystem2D, korzysta ona ze skryptu Turtle3D zamiast Turtle2D (chociaż są one na razie identyczne). Dodaj do Turtle3D obsługę obrotów w trzech wymiarach za pomocą znaków:

• & obrót do góry (pitch), czyli obrót względem osi X o kąt \delta
• ^ obrót do góry (pitch), czyli obrót względem osi X o kąt -\delta
• \ obrót do obrót w prawo (roll), czyli obrót względem osi Y o kąt -\delta
• / obrót do obrót w lewo (roll), czyli obrót względem osi Y o kąt \delta

Poza tym dla symboli L i F dodaj interpretacje kolejno jako liść i kwiat. W folderze Models są gotowe modele, ale możesz ściągnąć własne.

Wykorzystaj dotychczasową wiedzę i powyższą interpretację, by stworzyć L-System generujący roślinę polną jak poniższy chaber.