# Podsumowanie
Podsumowanie zajęć. Zadania z zajęć są na tym repozytorium. [Link](http://wolynski.home.amu.edu.pl/E4BC1/index.html) do strony z wykładami. DSTTLI Hasło: E4BC1
---
## LAB 1
Zakres:
- wstęp do języka R
- wykład 1 na stronie
### R
Lista:
```r
# wektory
rep(TRUE, 3)
seq(1, 20, by=1)
order(zad6, decreasing = TRUE)]
# pętle
for(i in 1:length(zad5)){}
while (licznik <= length(x)){}
repeat {
if (licznik > length(x)) {
break
}
}
# funkcja, pakiety
minmax <- function(x){}
install.packages("schoolmath")
library(schoolmath)
```
### Zagadnienia


---
## LAB 2
Zagadnienia:
- ciąg dalszy wprowadzenie do R
- wykład 1 na stronie
### R
Lista:
```r
# ładowanie danych
dane <- read.table("dane1.csv", header = TRUE, sep = ";")
load(url("http://ls.home.amu.edu.pl/data_sets/Centrala.RData"))
ankieta <- read.table("http://ls.home.amu.edu.pl/data_sets/ankieta.txt", header = TRUE)
computers <- read.csv("http://pp98647.home.amu.edu.pl/wp-content/uploads/2021/06/computers.csv")
```
### Zagadnienia
Lista:
- **Wektor** musi zawierać takie same typy, **lista** może różne.
- **Macierze**, ogólniej to są **tablice** reprezentowane przez wektor atomowy
- **Czynniki**: dla ("f", "p", "f") zwraca "f", "p"
- **Ramki danych** to jak w excelu arkusze
---
## LAB 3
Zagadnienia:
- **Statystka opisowa** - zaprezentowanie cechy X na próbce za pomocą tabeli, wykresu
- Wykład 2 na stronie
### R
```r
# rozkład empiryczny
ankieta <- read.table("http://ls.home.amu.edu.pl/data_sets/ankieta.txt", header = TRUE)
empiryczny <- data.frame(cbind(liczebnosc = table(ankieta$wynik),
procent = prop.table(table(ankieta$wynik))))
# wykres ramkowy
barplot(table(ankieta$wynik),
xlab = "Odpowiedzi", ylab = "Odpowiedzi",
main = "Rozkład empiryczny zmiennej wynik")
# inne
install.packages("e1071")
library(e1071)
skewness(x)
kurtosis(x)
```
### Zagadnienia
Lista:
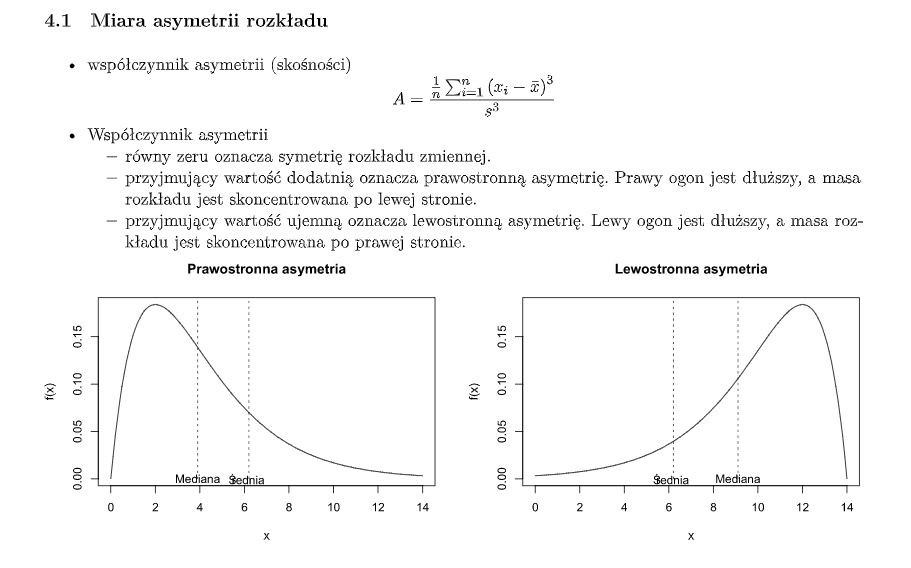
- **Miara asymetrii rozkładu** - w którą stronę - prawo/lewo, zmienna się rozkłada.
- zero to symetryczny
- dodatnie to prawostronnie asymetryczny - lewa część jest większa
- ujemna to lewostronnie asymetryczna - prawa część jest większa
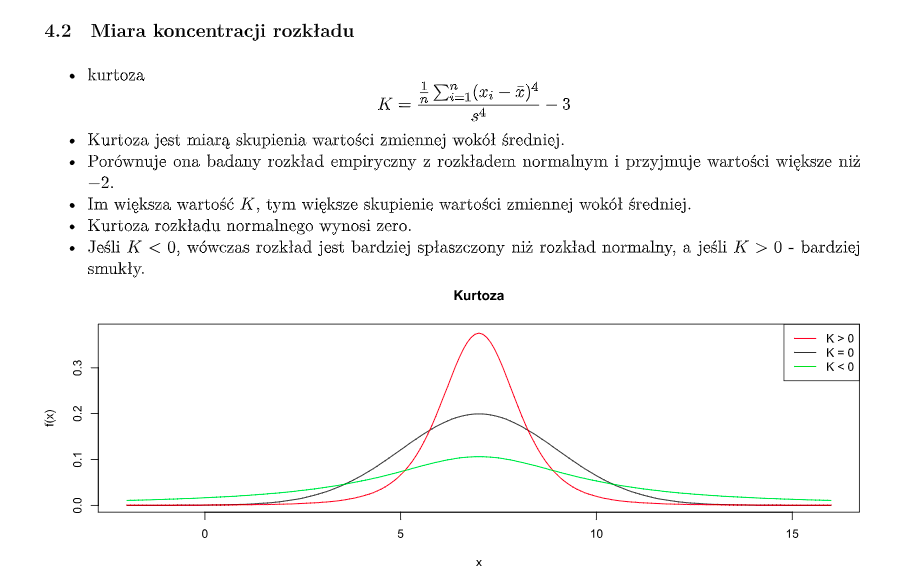
- **Kurtoza** - miara skupienia wartości wokół średniej. Porównuje rozkład empiryczny z rozkładem normalnym.
- Większa niż 0, im większa wartość tym bardziej wartości skupione wokół średniej
- Dla rozkładu normalnego = 0
- Dla ujemnych (min -2) wykres jest bardziej spłaszczony niż rozkłąd normalny
- **Odchylenie standardowe** - intuicyjnie rzecz ujmując, odchylenie standardowe mówi, jak szeroko wartości jakiejś wielkości (na przykład wieku, inflacji, kursu walutowego) są rozrzucone wokół jej średniej.
Im mniejsza wartość odchylenia tym obserwacje są bardziej skupione wokół średniej. Odchylenie standardowe z próby ma trochę inny wzór [link](https://pl.wikipedia.org/wiki/Odchylenie_standardowe#Odchylenie_standardowe_z_próby)
- **Współczynnik zmienności** - podaje się w procentach, jest to relacja odchylenia standardowego ze średnią. Mówi nam jak bardzo wartości odbiegają od siebie. Dzięki temu ze jest w procentach mozemy porównywać rózne rozkłady.
- [Przykład](https://pl.wikipedia.org/wiki/Współczynnik_zmienności)
- **Funkcja gęstości** - nieujemna funkcja rzeczywista, określona dla rozkładu prawdopodobieństwa, taka że całka z tej funkcji, obliczona w odpowiednich granicach, jest równa prawdopodobieństwu wystąpienia danego zdarzenia losowego.
- **Histogram** – składa się z szeregu prostokątów umieszczonych na osi współrzędnych. Prostokąty te są z jednej strony wyznaczone przez przedziały klasowe wartości cechy, natomiast ich wysokość jest określona przez liczebności (lub częstości, ewentualnie gęstość prawdopodobieństwa) elementów wpadających do określonego przedziału klasowego.
- **Kwantyl** rzędu p to taka zmienna dla której prawdopodobieństwo wystąpienia od 0 do tej zmiennej jest równe p.
Kwantyl rzędu 1/2 to inaczej mediana. Kwantyle rzędu 1/4, 2/4, 3/4 są inaczej nazywane kwartylami.
- pierwszy kwartyl (notacja: Q1) = dolny kwartyl = kwantyl rzędu 1/4 = 25% obserwacji jest położonych poniżej
- drugi kwartyl (notacja: Q2) = mediana = kwantyl rzędu 1/2 = dzieli zbiór obserwacji na połowę
- trzeci kwartyl (notacja: Q3) = górny kwartyl = kwantyl rzędu 3/4 = dzieli zbiór obserwacji na dwie części odpowiednio po 75% położonych poniżej tego kwartyla i 25% położonych powyżej

- **Wykres ramkowy**


- **Rozkład empiryczny** – uzyskany na podstawie badania statystycznego opis wartości przyjmowanych przez cechę statystyczną w próbie przy pomocy częstości ich występowania.
- Statystki opisowe - rodzaje

---
## LAB 4
Zagadnienia:
- rozkłady statystyczne
- wykład 3 i 4 na stronie
### R
```r
# odchylenie standardowe dla próby to musimy dodatkowo pomnozyc przez ten pierwiastek na koncu!!!
a_est_mm <- mean(czas_oczek_tramwaj) - sqrt(3) * sd(czas_oczek_tramwaj) * sqrt((length(czas_oczek_tramwaj) - 1) / (length(czas_oczek_tramwaj)))
barplot(counts,
xlab = "Liczba zgloszen", ylab = "Prawdopodobienstwo",
main = "Rozklady empiryczny i teoretyczny liczby zgloszen",
col = c("red", "blue"), legend = rownames(counts), beside = TRUE)
#kwanty-kwantyl, linia to moj estymator
qqplot(rpois(length(Centrala$Liczba), lambda = lambda_est), Centrala$Liczba,
xlab = "Kwantyle teoretyczne", ylab = "Kwantyle empiryczne",
main = "Wykres kwantyl-kwantyl dla liczby zgloszen")
qqline(Centrala$Liczba, distribution = function(probs) { qpois(probs, lambda = lambda_est) })
# odchylenie standardowe dla próby to musimy dodatkowo pomnozyc przez ten pierwiastek na koncu!!!
a_est_mm <- mean(czas_oczek_tramwaj) -
sqrt(3) * sd(czas_oczek_tramwaj) * sqrt((length(czas_oczek_tramwaj) - 1) / (length(czas_oczek_tramwaj)))
b_est_mm<- mean(czas_oczek_tramwaj) +
sqrt(3) * sd(czas_oczek_tramwaj) * sqrt((length(czas_oczek_tramwaj) - 1) / (length(czas_oczek_tramwaj)))
# metoda największej warygodności
a_est <- min(czas_oczek_tramwaj)
b_est <- max(czas_oczek_tramwaj)
# metoda najwiekszej warygodnosci
curve(dunif(x, a_est, b_est),
add = TRUE, col = "blue", lwd = 2)
#metoda momentów
curve(dunif(x, a_est_mm, b_est_mm),
add = TRUE, col = "green", lwd = 2)
# bootstrap
library(boot)
dane <- rnorm(100)
meanboot <- function(x,i)mean(x[i])
bmean=boot(dane,meanboot,1000)
hist(bmean$t-mean(dane),prob=T,main='')
curve(dnorm(x,0,1/sqrt(length(dane))),add=T,col='red')
# monte carlo
dane <- rnorm(100)
mcmean <- vector('numeric',1000)
for(i in 1:1000) mcmean[i] <- mean(rnorm(100))
hist(mcmean,prob=T,main='')
curve(dnorm(x,0,0.1),add=T,col='red')
```
### Rozkłady statystyczne
Jeżeli próbka jest reprezentatywna, to stanowi ona podstawę do wnioskowania o populacji z której pochodzi. Wnioskowanie takie wymaga zbudowania modelu “zachowania się” zmiennej (cechy) X w populacji. Budowa modelu polega na przyjęciu założenia o rozkładzie (teoretycznym) zmiennej X w populacji oraz traktowaniu obserwacji jako wartości tej zmiennej.
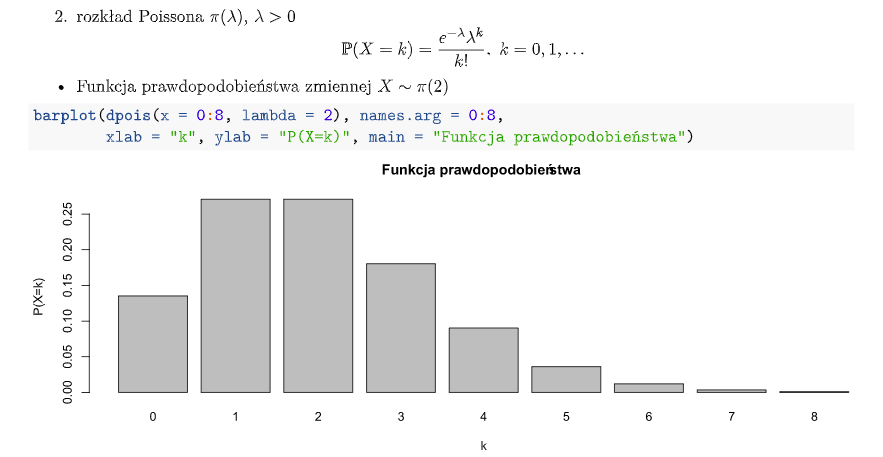
W wykresach na dole to wartość cechy a wysokość słupka to prawdopodobieństwo wystąpienia tej wartości.
- Rozkład Dwumianowy:

- Rozkład Poissona:
- Rozkład Jednostajny:


- Rozkład Normalny:

- Rozkład Wykładniczy:


- Rozkład Rayleigha:
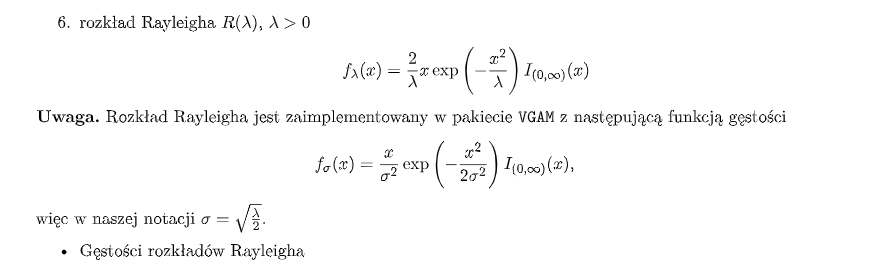

- Inne rozkłady:

### Zagadnienia
- Wykres kwantyl-kwantyl - służy do porównania dwóch rozkładów na podstawie kwantyli. Może służyć do porównania wartości estymowanych z rzeczywistymi. Punkt (x,y) odpowiada jednemu kwantylowi drugiego rodzaju - współrzędna y względem kwantyla tego samego rzędu pierwszego rozkładu - współrzędna x.

- Empiryczne - wynikające z doświadczenia
- Próba statystyczna – zbiór obserwacji statystycznych wybranych (zwykle wylosowanych) z populacji.
### Estymacja
- Estymator - statystyka (funkcja mierzalna określona na przestrzeni statystycznej) służąca do szacowania wartości parametru rozkładu.
- Estymator nieobciążony - wartość oczekiwana rozkładu estymatora jest równa wartości szacowanego parametru.
- Moment - moment zwykły rzędu k zmiennej losowej to wartość oczekiwana k-tej potęgi tej zmiennej.
- zmienna losowa to funkcja prawdopodobieństwa
- wartość oczekiwana to wartość określająca spodziewany wynik doświadczenia losowego. Dobrym estymatorem wartości oczekiwanej jest średnia.

- Metody wyznaczania estymatorów:
- Metoda momentów. Zwykle momenty uk są funkcjami parametrów. Tworzymy układ równań uk = estymator momentu


- Metoda największej wiarogodności

- Metoda Monte Carlo - losowanie, porównywanie


- Metoda bootstrapowa - mamy jakąś próbę z n obeserwacjami i z tej próby losujemy elementy - uzyskujemy próbkę bootstrapową. Powtarzając ten proces otrzymujemy ciąg próbek i odpowiadających jej wartości statystyki. Dzięki tej metodzie, wyniki testów parametrycznych i analiz opartych o modele liniowe są bardziej precyzyjne. Metoda szacowania (estymacji) wyników poprzez wielokrotne losowanie ze zwracaniem z próby. Przydatna gdy nie znamy typu rozkładu.

- Rozkłady estymatorów
- chi-kwadrat - rozkład zmiennej losowej, która jest sumą k kwadratów niezależnych zmiennych losowych o standardowym rozkładzie normalnym.

- Model wykładniczy

- Model normalny

---
## LAB 5
Zagadnienia:
- przedziały ufności
- wykład 5 na stronie
### R
```r
# klasyczne przedziały ufności
library(EnvStats)
epois(Centrala$Liczba,
method = "mle/mme/mvue",
ci = TRUE, ci.type = "two-sided", conf.level = 0.95,
ci.method = "exact")$interval$limits
eexp(Czas,ci=T)
# klasyczne przedziały ufności
load("Awarie.RData")
attach(Awarie)
m <- mean(Czas)
n <- length(Czas)
a <- 0.05
# chi-kwadrat
L <- qchisq(a/2,2*n)/(2*n*m)
R <- qchisq(1-(a/2),2*n)/(2*n*m)
# bootstrapowe przedziały ufności
library(boot)
load("Awarie.RData")
attach(Awarie)
lambdaboot <- function(x,i) 1/mean(x[i])
blambda <- boot(Czas,lambdaboot,1000)
boot.ci(blambda,conf=0.95,type='perc')
```
### Zagadnienia
- Estymacja przedziałowa - np jakieś urządzenie moze działać na pewnym przedziale wartości.
- Chcemy "złapać" jakąś wartość w przedział. Jest to lepsze niz próba oszacowania dokładnej wartości.
Jeżeli konstruujemy jakiś przedział z poziomem ufności 0,95 to na 100 prób w 95 nasz parametr jest w przedziale.
- Na podstawie funkcji centralnej mozemy stworzyć przedziały ufności. Funkcję centralną bierzemy z tabelki.
Podstawiamy funkcję centralną do prawdopodobieństwa oraz 1-a, wsadzamy parametr pomiędzy funkcję i wyliczamy a i b. a i b to przedział ufności. Jest przykład w pdfie w labach 5.

- Rozkład t-Studenta - kolejny typ rozkładu. Podobny to rozkładu normalnego. Rozkład t studenta stosujemy tylko w sytuacji, gdy odchylenie standardowe populacji jest nieznane, a rozmiar próby(ilość obserwacji) jest mniejsza niż 30. W przypadku gdy rozmiar próby jest większy lub równy 30 wtedy zamiast brać rozkład t bierzemy rozkład normalny. Wynika to z faktu, że rozkład t studenta dla 𝑛≥30 jest bardzo podobny do rozkładu normalnego. Dla n < 30 rozkład studenta jest „szerszy”, tzn. bardziej prawdopodobne są wartości mocno odbiegające od średniej niż w przypadku rozkładu normalnego.

- Dodatkowe

- Bootstrapowe przedziały ufności - po prostu przedział ufności z próbki bootstrapowej. (Z niewielkiej próby tworzymy losując ze zwracaniem zestaw wielu prób)

---
## LAB 6
Zagadnienia:
- testy statystyczne, testowanie hipotez statystycznych
- testy t-studenta
- wykład 6 i 7 na stronie
### R
```r
x <- c(78.2, 78.5, 75.6, 78.5, 78.5, 77.4, 76.6)
y <- c(76.1, 75.2, 75.8, 77.3, 77.3, 77.0, 74.4, 76.2, 73.5, 77.4)
boxplot(x, y)
shapiro.test(x)$p.value
qqnorm(x)
qqline(x)
shapiro.test(y)$p.value
qqnorm(y)
qqline(y)
var(x)
var(y)
var.test(x, y, alternative = "less")$p.value
```
## Testy statystyczne
- Testujemy czy wartość parametru jest istotnie różna od zadanej wartości. Musimy podać hipotezę alternatywną - działanie które podejmujemy jeśli hipoteza zerowa jest fałszywa.
- Obszary krytyczne

- Błędy pierwszego i drugiego rodzaju. Przez to możemy podjąć dwie decyzje - "odrzucamy hipotezę zerową" lub "nie ma podstaw do odrzucenia hipotezy zerowej".
- Odrzucamy hipotezę zerową gdy jest ona prawdziwa - błąd I rodzaju.
- Przyjmujemy hipotezę zerową gdy jest ona fałszywa - błąd II rodzaju.
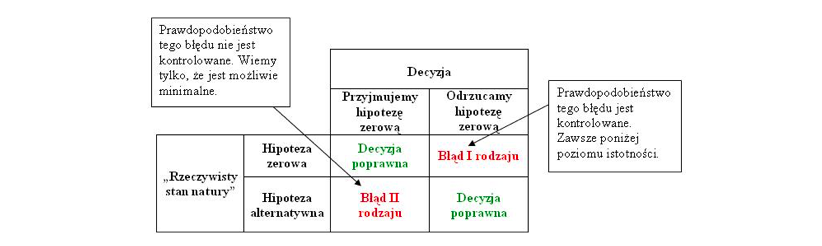
- Wybór wartości krytycznej - Ustalamy poziom istotności testu α i dobieramy wartość krytyczną tak, aby
- prawdopodobieństwo popełnienia błędu I rodzaju było mniejsze lub równe α,
- prawdopodobieństwo popełnienia błędu II rodzaju było minimalne.
- Testy ilorazu wiarogodności

### Zagadnienia
- P-wartość (p-value) to graniczny poziom istotności - najmniejszy, przy którym zaobserwowana wartość statystyki testowej prowadzi do odrzucenia hipotezy zerowej. Im p-wartość jest większa, tym bardziej hipoteza H0 jest prawdziwa. Im mniejsza tym niej prawdopodobna jest hipoteza H0. Wartość p, p-wartość, prawdopodobieństwo testowe. Sposoby obliczania z obszaru:
- Prawostronny obszar krytyczny
- Lewostronny obszar krytyczny
- Dwustronny obszar krytyczny
- Test t Studenta jest metodą statystyczną służącą do porównania dwóch średnich między sobą jeśli znamy liczbę badanych osób, średnią arytmetyczną oraz wartość odchylenia standardowego lub wariancji.
Jest to jeden z mniej skomplikowanych i bardzo często wykorzystywanych testów statystycznych używanych do weryfikacji hipotez. Dzięki niemu możemy dowiedzieć się czy dwie różne średnie są różne niechcący (w wyniku przypadku) czy są różne istotnie statystycznie (np. z uwagi na naszą manipulację eksperymentalna).
Są gotowe wzory do których podstawiamy wartości w zalezności od rodzaju próby. **Przykład w pdf w labach 6 - dla jednej próby lub dla dwóch wzory są na stronie**.
- Założenie normalności rozkładów błędów możemy (ewentualnie) zastąpić założeniem mówiącym o dysponowaniu dużą próbą, tzn.
- Próby niezależne - obserwacje w poszczególnych populacjach (grupach) dokonywane są na różnych jednostkach eksperymentalnych.
- Próby zależne - obserwacje dokonywane są dwukrotnie na tych samych jednostkach eksperymentalnych.
- Test Shapiro-Wilka- hipotezy:
- H0 : Próba pochodzi z populacji o rozkładzie normalnym
- H1 : Próba nie pochodzi z populacji o rozkładzie normalnym.
Hipoteza zerowa tego testu mówi nam o tym, że nasza próba badawcza pochodzi z populacji o normalnym rozkładzie. Jeśli test Shapiro-Wilka osiąga istotność statystyczną (p < 0,05), świadczy to o rozkładzie oddalonym od krzywej Gaussa. W przypadku tego testu najczęściej chcemy otrzymać wartości nieistotne statystyczne (p > 0,05), ponieważ świadczą one o zgodności rozkładu zmiennej z rozkładem normalnym.
- Var.test (test F dla dwóch wariancji) - wariancja - Intuicyjnie utożsamiana ze zróżnicowaniem zbiorowości. Wg dokumentacji jest to test pozwalający porównać wariancje z dwóch rozkładów normalnych.
---
## LAB 7
Zagadnienia:
- analiza wariancji ANOVA - w skróce badanie zależności między obserwacjami
- wykład 8 na stronie
### R
```r
# założenia
rests <- lm(number ~ context, data = dane)$residuals
shapiro.test(rests)$p.value
qqnorm(rests)
qqline(rests)
bartlett.test(number ~ context, data = dane)$p.value
fligner.test(number ~ context, data = dane)$p.value
library(car)
leveneTest(number ~ context, data = dane)[[3]][1]
leveneTest(number ~ context, data = dane, center = "mean")[[3]][1]
# jednoczynnikowa ANOVA
summary(aov(number ~ context, data = dane))
# testy post-hoc
pairwise.t.test(number, context, data = dane)
TukeyHSD(model_aov)$context
plot(TukeyHSD(model_aov))
install.packages("agricolae")
library(agricolae)
HSD.test(model_aov, "context", console = TRUE)
SNK.test(model_aov, "context", console = TRUE)
LSD.test(model_aov, "context", p.adj = "holm", console = TRUE)
scheffe.test(model_aov, "context", console = TRUE)
# kontrasty
C1 <- c(-3, 2, 2, -3, 2)
C2 <- c(0, -1, -1, 0, 2)
C3 <- c(0, 1, -1, 0, 0)
C4 <- c(1, 0, 0, -1, 0)
con <- cbind(C1, C2, C3, C4)
contrasts(dane$context) <- con
model_aov_2 <- aov(number ~ context, data = dane)
summary(model_aov_2, split = list(context = list('C1' = 1, 'C2' = 2, 'C3' = 3, 'C4' = 4)))
```
### Wstęp
- Analiza wariancji ANOVA - metoda statystyczna służąca do badania obserwacji, które zależą od jednego lub wielu działających równocześnie czynników. Metoda ta wyjaśnia, z jakim prawdopodobieństwem wyodrębnione czynniki mogą być powodem różnic między obserwowanymi średnimi grupowymi.
- Modele jednoczynnikowe – wpływ każdego czynnika jest rozpatrywany oddzielnie, tą klasą zagadnień zajmuje się jednoczynnikowa analiza wariancji. Chcemy sprawdzić, czy jakiś pojedynczy czynnik ma wpływ na mierzoną zmienną zależną.
- Modele wieloczynnikowe – wpływ różnych czynników jest rozpatrywany łącznie, tą klasą zagadnień zajmuje się wieloczynnikowa analiza wariancji.
### Jednoczynnikowa analiza wariancji
Na test jednoczynnikowej analizy wariancji możemy patrzeć jak na uogólnienie testu t-Studenta dla więcej niż 2 prób niezależnych.

- Wyniki przedstawiamy w postaci tabeli
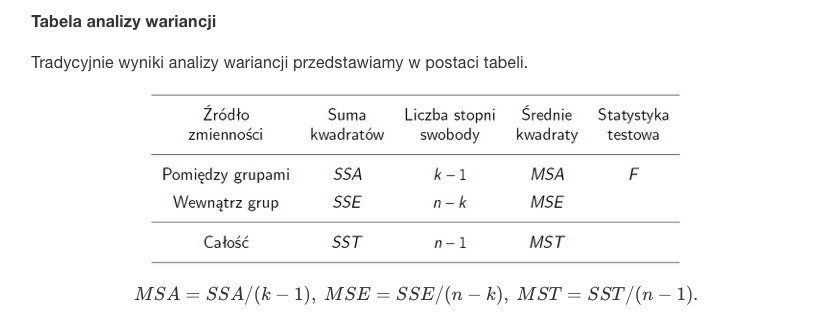
- Założenia:
- Niezależność obserwacji dla poszczególnych jednostek eksperymentalnych.
- Błędy mają rozkłady normalne z zerową wartością oczekiwaną (brak błędu systematycznego) i jednorodną wariancją. - to możemy sprawdzić **testem Bartletta**
## Testy post hoc
Testy post-hoc (po fakcie) wykonuje się jako kolejny krok analizy wariancji. Znane są również pod nazwą porównań wielokrotnych lub porównań parami. Sama analiza wariancji mówi nam o tym czy różnice w porównywanych średnich występują czy nie. Nie wiemy jednak między którymi grupami zachodzą te różnice. Istotny współczynnik F wskazuje jedynie na słuszność (lub brak słuszności) odrzucenia hipotezy zerowej. Jeśli ją odrzucimy musimy dowiedzieć się czy wszystkie średnie różnią się między sobą czy tylko niektóre. Stąd też nazwa “po fakcie” – wykonujemy je dopiero po sprawdzeniu czy wynik F jest istotny statystycznie. Jeśli nie jest, nie musimy wykonywać testów post-hoc.
- Procedura NIR – Fishera.

- Tukey, test HSD i SNK są pochodnymi Tukeya

- LSD - Multiple comparisons, "Least significant difference" and Adjust P-values. Wynik też grupy.
- Scheffe - method is very general in that all possible contrasts can be tested for significance and confidence intervals can be constructed for the corresponding linear. The test is conservative. Wynik też grupy.
- pairwise.t.test - daje wynik w postaci tabeli jak różnią się od siebie wyniki poszczególnych grup
### Zagadnienia
- bartlett.test, fligner.test oraz leveneTest użyte do sprawdzenia czy wariancje dwóch grup są takie same.

- Układ losowych bloków kompletnych. W celu wyeliminowania niejednorodności jednostek eksperymentalnych możemy pogrupować je w bloki. Po prostu przed testami grupujemy.
- Jednoczynnikowa ANOVA - układ doświadczalny. Na stronie analiza wariancji była wytłumaczona bardziej opisowo - na podstawie analogii do układu doświadczalengo.
- Kontrasty - by można było zdefiniować wybrane hipotezy należy dla każdej średniej przypisać wartość kontrastu.
Wartości kontrastu są tak wybierane by ich sumy dla porównywanych stron były liczbami przeciwnymi, a ich wartość dla średnich nie biorących udziału w analizie wynosi 0!!
Wykonując później test ANOVA - analiza wariancji możemy zobaczyć czy porównywane grupy (wyszczególnione za pomocą kontrastów) różnią się od siebie.
- Ortogonalny - prostopadły
---
## LAB 8
Zagadnienia:
-
### R
### Zagadnienia
---
## LAB 9
Zagadnienia:
-
### R
### Zagadnienia