# Podsumowanie
Podsumowanie zajęć. Zadania z zajęć są na tym repozytorium. [Link](http://wolynski.home.amu.edu.pl/E4BC1/index.html) do strony z wykładami. DSTTLI Hasło: E4BC1



---
## LAB 1
Zakres:
- wstęp do języka R

- wykład 1 na stronie



### R
Lista:
```r
# wektory
rep(TRUE, 3)
seq(1, 20, by=1)
order(zad6, decreasing = TRUE)]

# pętle
for(i in 1:length(zad5)){}
while (licznik <= length(x)){}
repeat {
  if (licznik > length(x)) {
    break
  }
}

# funkcja, pakiety
minmax <- function(x){}
install.packages("schoolmath")
library(schoolmath)
```

### Zagadnienia
![operatory](lab1/operatory.png)

![logiczne](lab1/logiczne.png)


---
## LAB 2
Zagadnienia:
- ciąg dalszy wprowadzenie do R

- wykład 1 na stronie



### R
Lista:
```r
# ładowanie danych
dane <- read.table("dane1.csv", header = TRUE, sep = ";")
load(url("http://ls.home.amu.edu.pl/data_sets/Centrala.RData"))
ankieta <- read.table("http://ls.home.amu.edu.pl/data_sets/ankieta.txt", header = TRUE)
computers <- read.csv("http://pp98647.home.amu.edu.pl/wp-content/uploads/2021/06/computers.csv")
```


### Zagadnienia
Lista:
- **Wektor** musi zawierać takie same typy, **lista** może różne.

- **Macierze**, ogólniej to są **tablice** reprezentowane przez wektor atomowy

- **Czynniki**: dla ("f", "p", "f") zwraca "f", "p"

- **Ramki danych** to jak w excelu arkusze


---
## LAB 3
Zagadnienia:
- **Statystka opisowa** - zaprezentowanie cechy X na próbce za pomocą tabeli, wykresu

- Wykład 2 na stronie


### R
```r
# rozkład empiryczny
ankieta <- read.table("http://ls.home.amu.edu.pl/data_sets/ankieta.txt", header = TRUE)
empiryczny <- data.frame(cbind(liczebnosc = table(ankieta$wynik),
                               procent = prop.table(table(ankieta$wynik))))

# wykres ramkowy
barplot(table(ankieta$wynik),
        xlab = "Odpowiedzi", ylab = "Odpowiedzi",
        main = "Rozkład empiryczny zmiennej wynik")

# inne
install.packages("e1071")
library(e1071)
skewness(x)
kurtosis(x)
```


### Zagadnienia
Lista:
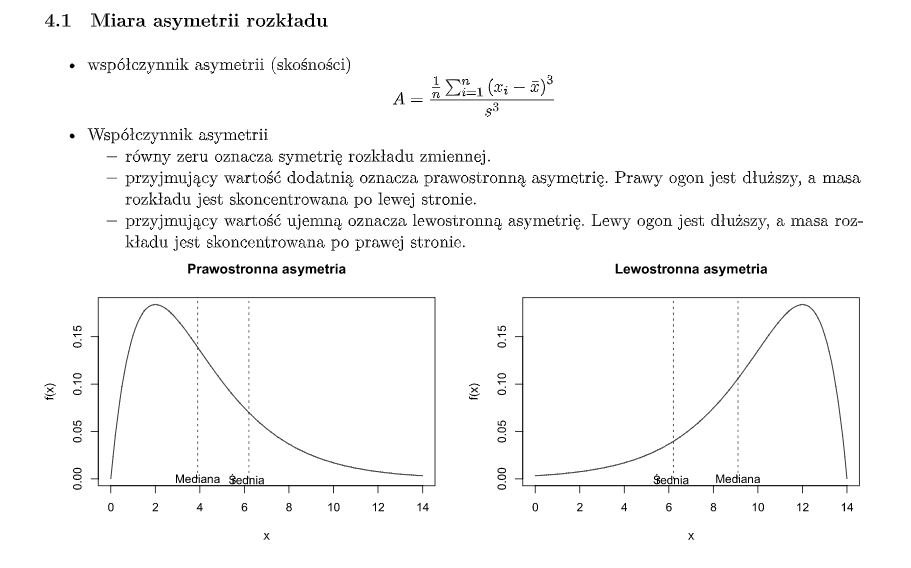
- **Miara asymetrii rozkładu** - w którą stronę - prawo/lewo, zmienna się rozkłada.
    - zero to symetryczny
    - dodatnie to prawostronnie asymetryczny - lewa część jest większa
    - ujemna to lewostronnie asymetryczna - prawa część jest większa
![asymetria](lab3/asymetria.png)

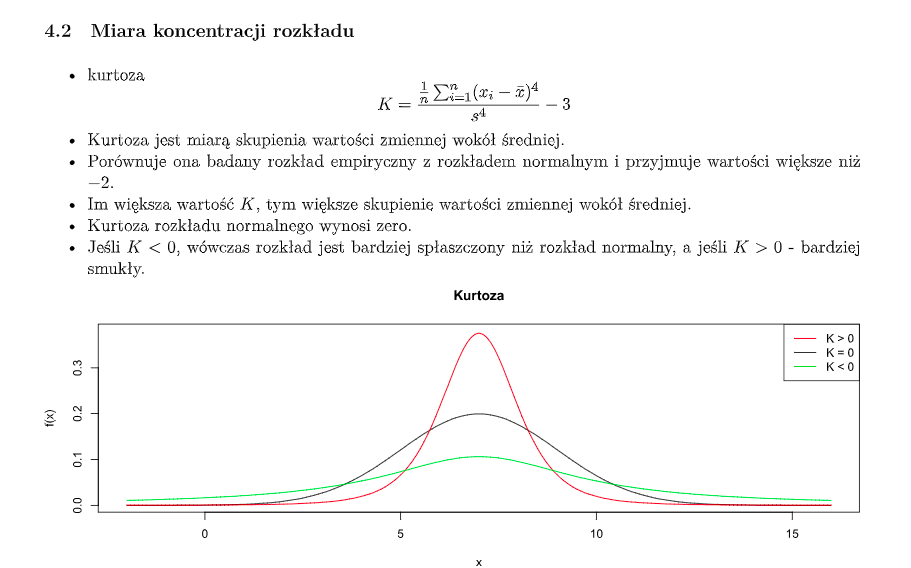
- **Kurtoza** - miara skupienia wartości wokół średniej. Porównuje rozkład empiryczny z rozkładem normalnym.
    - Większa niż 0, im większa wartość tym bardziej wartości skupione wokół średniej
    - Dla rozkładu normalnego = 0
    - Dla ujemnych (min -2) wykres jest bardziej spłaszczony niż rozkłąd normalny
![kurtoza](lab3/kurtoza.png)

- **Odchylenie standardowe** - intuicyjnie rzecz ujmując, odchylenie standardowe mówi, jak szeroko wartości jakiejś wielkości (na przykład wieku, inflacji, kursu walutowego) są rozrzucone wokół jej średniej.
Im mniejsza wartość odchylenia tym obserwacje są bardziej skupione wokół średniej. Odchylenie standardowe z próby ma trochę inny wzór [link](https://pl.wikipedia.org/wiki/Odchylenie_standardowe#Odchylenie_standardowe_z_próby)

- **Współczynnik zmienności** - podaje się w procentach, jest to relacja odchylenia standardowego ze średnią. Mówi nam jak bardzo wartości odbiegają od siebie. Dzięki temu ze jest w procentach mozemy porównywać rózne rozkłady.
    - [Przykład](https://pl.wikipedia.org/wiki/Współczynnik_zmienności)
<br/><br/>

- **Funkcja gęstości** - nieujemna funkcja rzeczywista, określona dla rozkładu prawdopodobieństwa, taka że całka z tej funkcji, obliczona w odpowiednich granicach, jest równa prawdopodobieństwu wystąpienia danego zdarzenia losowego.

- **Histogram** – składa się z szeregu prostokątów umieszczonych na osi współrzędnych. Prostokąty te są z jednej strony wyznaczone przez przedziały klasowe wartości cechy, natomiast ich wysokość jest określona przez liczebności (lub częstości, ewentualnie gęstość prawdopodobieństwa) elementów wpadających do określonego przedziału klasowego.

- **Kwantyl** rzędu p to taka zmienna dla której prawdopodobieństwo wystąpienia od 0 do tej zmiennej jest równe p.
Kwantyl rzędu 1/2 to inaczej mediana. Kwantyle rzędu 1/4, 2/4, 3/4 są inaczej nazywane kwartylami.
    - pierwszy kwartyl (notacja: Q1) = dolny kwartyl = kwantyl rzędu 1/4 = 25% obserwacji jest położonych poniżej
    - drugi kwartyl (notacja: Q2) = mediana = kwantyl rzędu 1/2 = dzieli zbiór obserwacji na połowę
    - trzeci kwartyl (notacja: Q3) = górny kwartyl = kwantyl rzędu 3/4 = dzieli zbiór obserwacji na dwie części odpowiednio po 75% położonych poniżej tego kwartyla i 25% położonych powyżej
![kwanty](lab3/kwantyl.png)

- **Wykres ramkowy**<br/>
![ramkowy1](lab3/ramkowy1.png)
![ramkowy2](lab3/ramkowy2.png)

- **Rozkład empiryczny** – uzyskany na podstawie badania statystycznego opis wartości przyjmowanych przez cechę statystyczną w próbie przy pomocy częstości ich występowania.

- Statystki opisowe - rodzaje<br/>
![dodatek](lab3/dodatek.png)



---
## LAB 4
Zagadnienia:
- rozkłady statystyczne

- wykład 3 i 4 na stronie



### R
```r
# odchylenie standardowe dla próby to musimy dodatkowo pomnozyc przez ten pierwiastek na koncu!!!
a_est_mm <- mean(czas_oczek_tramwaj) - sqrt(3) * sd(czas_oczek_tramwaj) * sqrt((length(czas_oczek_tramwaj) - 1) / (length(czas_oczek_tramwaj)))

barplot(counts, 
        xlab = "Liczba zgloszen", ylab = "Prawdopodobienstwo",
        main = "Rozklady empiryczny i teoretyczny liczby zgloszen",
        col = c("red", "blue"), legend = rownames(counts), beside = TRUE)

#kwanty-kwantyl, linia to moj estymator
qqplot(rpois(length(Centrala$Liczba), lambda = lambda_est), Centrala$Liczba,
       xlab = "Kwantyle teoretyczne", ylab = "Kwantyle empiryczne",
       main = "Wykres kwantyl-kwantyl dla liczby zgloszen")
qqline(Centrala$Liczba, distribution = function(probs) { qpois(probs, lambda = lambda_est) })
```


### Rozkłady statystyczne
Jeżeli próbka jest reprezentatywna, to stanowi ona podstawę do wnioskowania o populacji z której pochodzi. Wnioskowanie takie wymaga zbudowania modelu “zachowania się” zmiennej (cechy) X w populacji. Budowa modelu polega na przyjęciu założenia o rozkładzie (teoretycznym) zmiennej X w populacji oraz traktowaniu obserwacji jako wartości tej zmiennej.
<br/><br/>

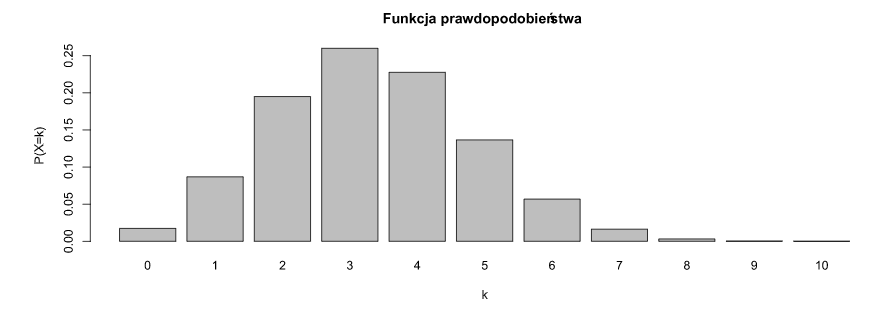
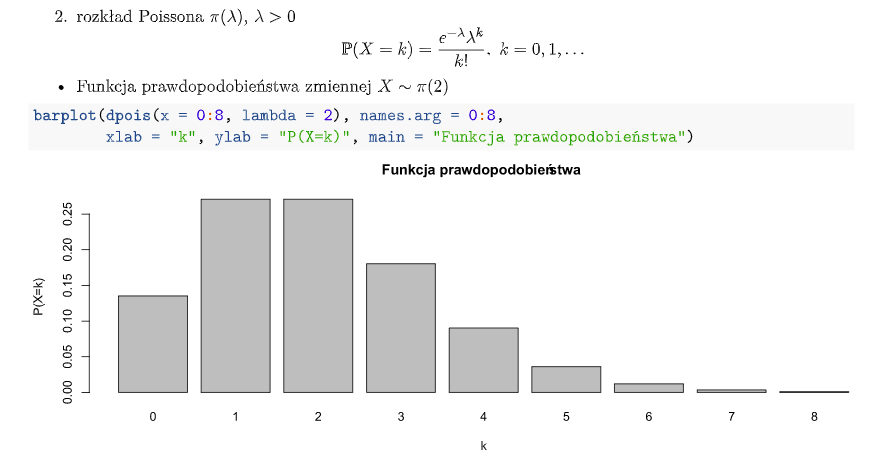
W wykresach na dole to wartość cechy a wysokość słupka to prawdopodobieństwo wystąpienia tej wartości.

- Rozkład Dwumianowy:<br/>
![dwumianowy](lab4/dwumianowy.png)
![dwumianowy2](lab4/dwumianowy2.png)

- Rozkład Poissona:<br/>
![poissona](lab4/poissona.png)

- Rozkład Jednostajny:<br/>
![jednostajny](lab4/jednostajny.png)
![jednostajny2](lab4/jednostajny2.png)

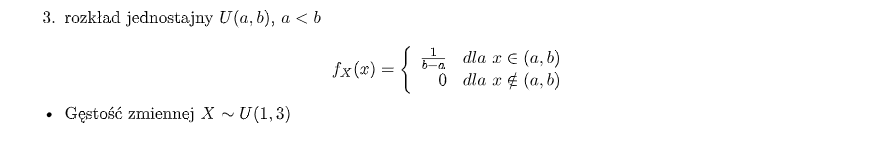
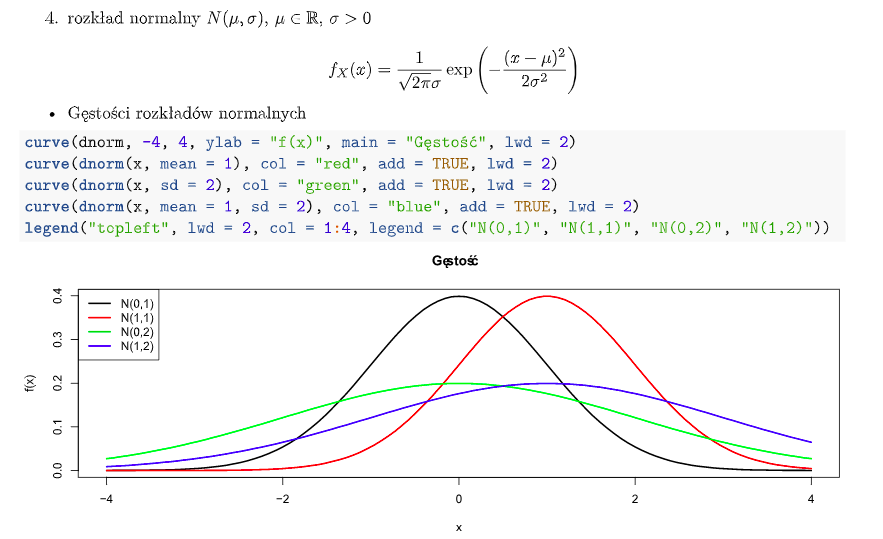
- Rozkład Normalny:<br/>
![normalny](lab4/normalny.png)

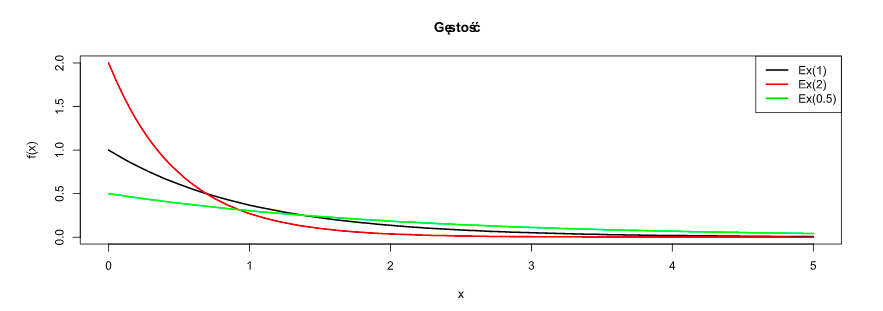
- Rozkład Wykładniczy:<br/>
![wykladniczy](lab4/wykladniczy.png)
![wykladniczy2](lab4/wykladniczy2.png)

- Rozkład Rayleigha:<br/>
![rayleigh](lab4/rayleigh.png)
![rayleigh2](lab4/rayleigh2.png)

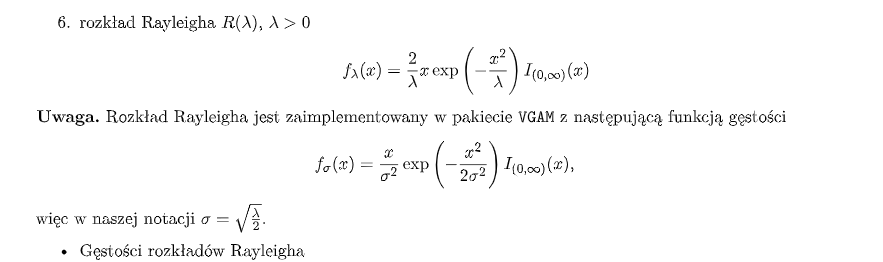
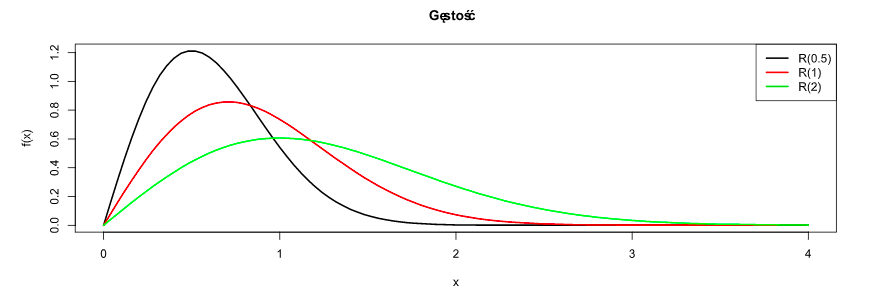
- Inne rozkłady:<br/>
![inne](lab4/inne.png)


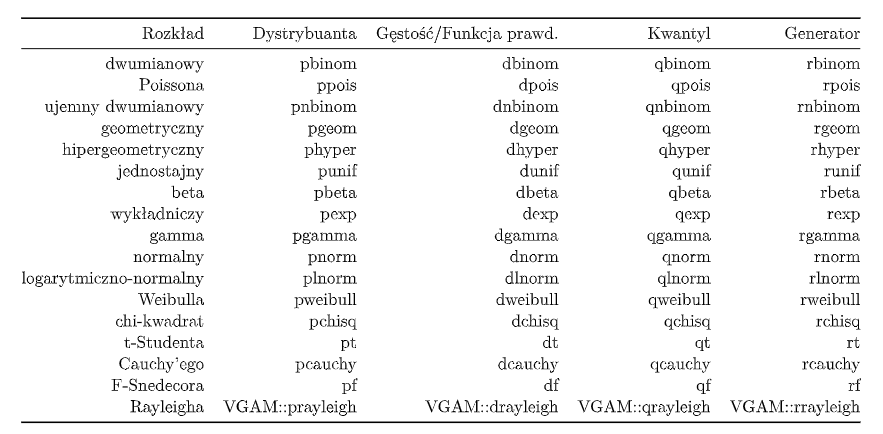
### Zagadnienia
- Wykres kwantyl-kwantyl - służy do porównania dwóch rozkładów na podstawie kwantyli. Może służyć do porównania wartości estymowanych z rzeczywistymi. Punkt (x,y) odpowiada jednemu kwantylowi drugiego rodzaju - współrzędna y względem kwantyla tego samego rzędu pierwszego rozkładu - współrzędna x.
![kwantylkwantyl](lab4/kwantylkwantyl.png)

- Empiryczne - wynikające z doświadczenia



### Estymacja
- estymator 

- estymator nieobciążony

- Estymatorem największej wiarogodności

- metody wyznaczania estymatorów

    - Metoda momentów

    - Metoda największej wiarogodności

    - Metoda Monte Carlo

    - Metoda bootstrapowa


- Rozkłady estymatorów

    - chi-kwadrat

    - Model wykładniczy

    - Model normalny



---
## LAB 5
Zagadnienia:
- przedziały ufności

- wykład 5 na stronie



### R


### Zagadnienia



---
## LAB 6
Zagadnienia:
- testy statystyczne, testowanie hipotez statystycznych

- testy t-studenta

- wykład 6 i 7 na stronie



### R


### Zagadnienia