DSZI_Survival/GeneticAlgorithm.md

Algorythm Genetyczny w projekcie DSZI_Survival

Autor: Marcin Kostrzewski

---

Cel

Celem algorytmu jest znalezienie czterech optymalnych wartości, według których agent podejmuje decyzję, co zrobić dalej. Te cztery cechy to:

• Priorytet (chęć) zaspokajania głodu,
• Zaspokajanie pragnienia,
• Odpoczynek,
• Jak odległość od obiektu wpływa na podjętą decyzję.

Zestaw tych cech reprezentuje klasa-struktura Affinities:

class Affinities:
    def __init__(self, food, water, rest, walking):
        """
        Create a container of affinities. Affinities describe, what type of entities a player prioritizes.
        :param food: Food affinity
        :param water: Freshwater affinity
        :param rest: Firepit affinity
        :param walking: How distances determine choices
        """
        self.food = food
        self.water = water
        self.rest = rest
        self.walking = walking

Oczywiście agent (gracz) posiada w swojej klasie pole self.affinities.

Podejmowanie decyzji

Gracz podejmuje decyzję o wyborze celu według następującej formuły:

typeWeight / (distance / walkingAffinity) * affectedStat * multiplier

gdzie:

• typeWeight - wartość cechy odpowiadającej typowi celu,
• distance - odległość od celu,
• walkingAffinity - waga odległości,
• affectedStat - aktualna wartość odpowiadającej statystyki agenta,
• multiplier - mnożnik redukujący wpływ obecnych statystyk na wybór.

Implementacja w GA.py/pickEntity() (przykładowo dla jedzenia):

watersWeights = []
thirst = player.statistics.thirst
for water in waters:
    typeWeight = weights[1]
    distance = abs(player.x - water.x) + abs(player.x - water.y)
    watersWeights.append(typeWeight / (distance * walkingAffinity) * thirst * 0.01)

Dla każdego obiektu, z którym agent może podjąć interakcję wyliczana jest ta wartość i wybierany jest obiekt, dla którego jest największa.

Implementacja algorytmu genetycznego

Za realizację algorytmu odpowiada funkcja geneticAlgorithm() w GA.py (Skrócona wersja):

def geneticAlgorithm(map, iter, solutions, mutationAmount=0.05):
    # Based on 4 weights, that are affinities tied to the player
    weightsCount = 4

    # Initialize the first population with random values
    initialPopulation = numpy.random.uniform(low=0.0, high=1.0, size=(solutions, weightsCount))
    population = initialPopulation

    for i in range(iter):
        fitness = []
        for player in population:
            fitness.append(doSimulation(player, map))

        parents = selectMatingPool(population, fitness, int(solutions / 2))

        offspring = mating(parents, solutions, mutationAmount)

        population = offspring

Omówienie:

Pierwsza populacja

Pierwsza populacja inicjalizowana jest losowymi wartościami. Szukamy czterech najlepszych wag; każdy osobnik z gatunku jest reprezentowany przez listę 4-elementową wag.

initialPopulation = numpy.random.uniform(low=0.0, high=1.0, size=(solutions, weightsCount))

Rozpoczyna się pętla, która stworzy tyle generacji, ile sprecyzujemy w parametrze.

Symulacja i fitness

Dla każdego osobnika z populacji uruchamiana jest symulacja. Symulacja dzieje się w tle, żeby zminimializować czas potrzebny do wykonania pełnej symulacji. Jej koniec następuje w momencie, gdy agent umrze.

fitness.append(doSimulation(player, map))

Wartością zwracaną przez funkcję symulacji jest tzw. fitness. W tym wypadku, wartością tą jest ilość kroków, jakie pokonał agent przez cykl życia.

Wybór rodziców

Rodzice dla dzieci przyszłego pokolenia wybierani są na podstawie wartości fitness. W tym wypadku wybirana jest połowa populacji z najwyższymi wartościami przeżywalności.

parents = selectMatingPool(population, fitness, int(solutions / 2))

Potomstwo, czyli rozmnażanie i mutacje

Za wyliczanie wartości dla nowego pokolenia odpowiada funkcja mating. Przekazujemy do niej rodziców, ilość potomstwa i siłę mutacji. Z GA.py/mating():

for i in range(offspringCount):
    parent1 = i % len(parents)
    parent2 = (i + 1) % len(parents)
    offspring.append(crossover(parents[parent1], parents[parent2]))

Do stworzenia potomstwa używana jest funkcja crossover, która wylicza wartości, jakie przyjmie nowe potomstwo. Wartośc ta to mediana wartości obu rodziców. Z GA.py/crossover():

for gene1, gene2 in zip(genes1, genes2):
    result.append((gene1 + gene2) / 2)

Po zastosowaniu krzyżówki, jeden losowo wybrany gen jest alterowany o niewielką wartość (mutacja). Z GA.py/mutation():

for player in offspring:
    randomGeneIdx = random.randrange(0, len(player))
    player[randomGeneIdx] = player[randomGeneIdx] + random.uniform(-1.0, 1.0) * mutationAmount

Nowe potomstwo zastępuje obecną populacje i algorytm wchodzi w kolejną pętle:

population = offspring

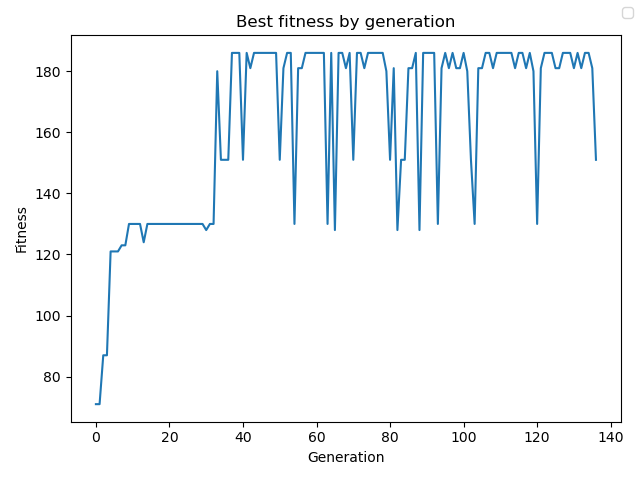
Skuteczność algorytmu

Zastosowanie algorytmu przynosi niezbyt spektakularne, lecz oczekiwane wyniki. Po uruchomieniu symulacji dla 1000 generacji:

• Wykres wartości fitness od generacji:

• Najlepsze / najgorsze fitness:

Best Fitness: 186
Worst Fitness: 71

• Zestaw najlepszych / najgorszych wartości

Best:
Affinities: food=0.9659207331357987, water=1.06794833921562, rest=0.4224083038045297, walking=0.26676612275274836
Worst:
Affinities: food=0.3927852322929111, water=0.6888704071372844, rest=0.625376993269597, walking=0.5415515638814266

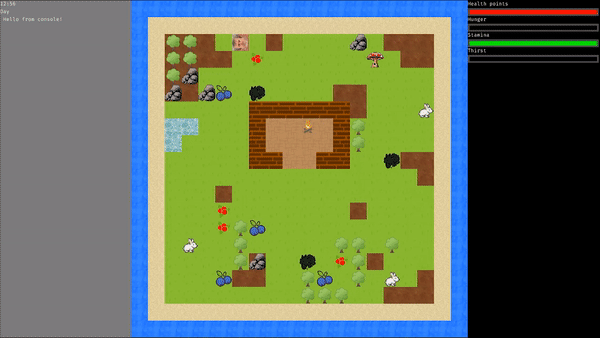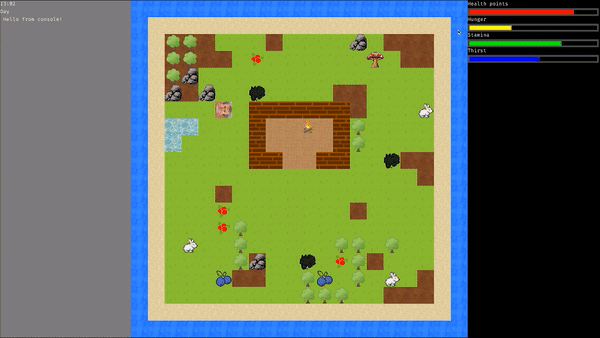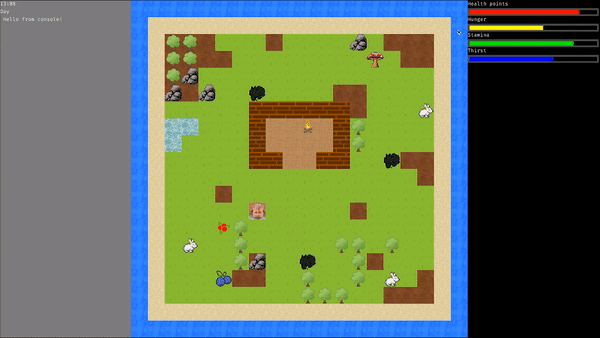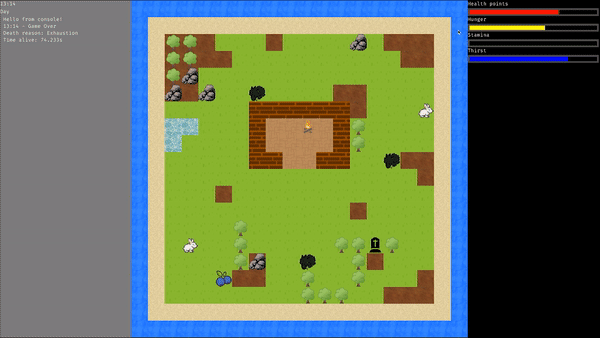
Przykład symulacji dla najlepszego osobnika:

Zastosowanie w całości projektu

Dzięki wyliczonym przez algorytm wagom, gracz poruszający się w środowisku będzie znał swoje priorytety i będzie w stanie przeżyć jak najdłużej. Obecnie, wybór obiektu jest dość statyczny i niezbyt "mądry", został napisany jedynie na potrzeby tego projektu. W przyszłości algorytm może być trenowany według inteligentnych wyborów obiektów np. poprzez zastosowanie drzewa decyzyjnego. Każdy obiekt ma zdefiniowany swój skutek, czyli gracz z góry wie, czym jest dany obiekt. W przyszłości gracz może nie znać informacji o obiektach, może być do tego używany jakiś inny algorytm, który oceni, czym jest dany obiekt.