data input correction and implement butter_lowpass_filter
This commit is contained in:
parent
8d17ca67e6
commit
ac8d1788e4
Binary file not shown.
|
Before 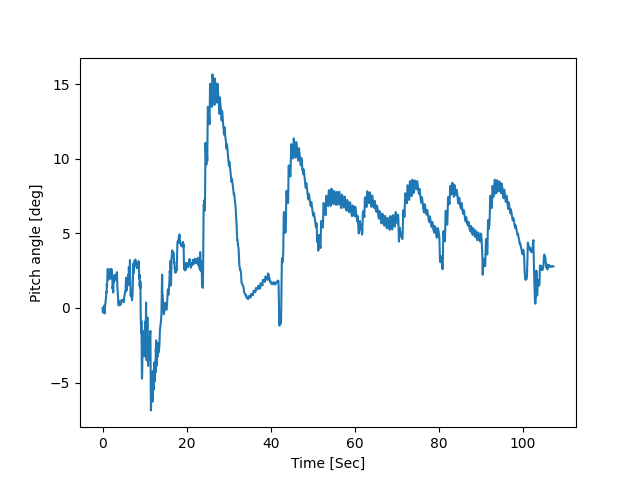
(image error) Size: 31 KiB After 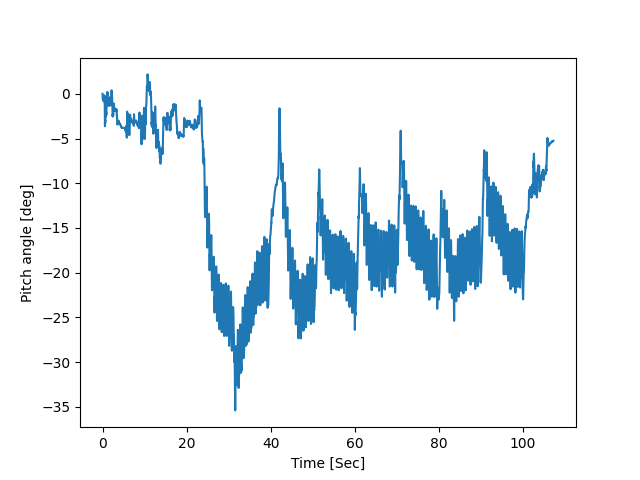
(image error) Size: 34 KiB 

|
Binary file not shown.
|
Before 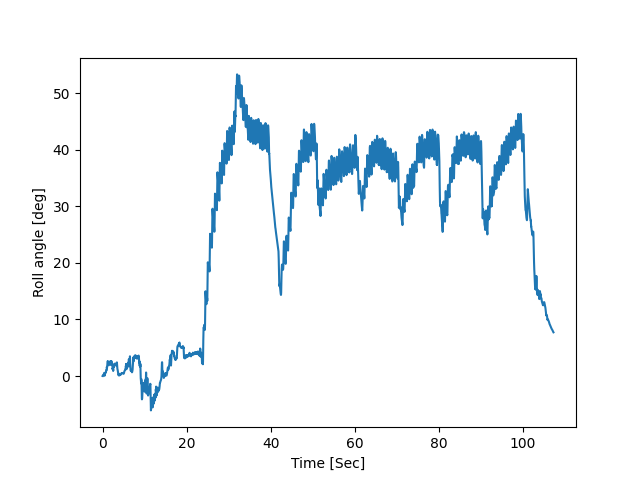
(image error) Size: 31 KiB After 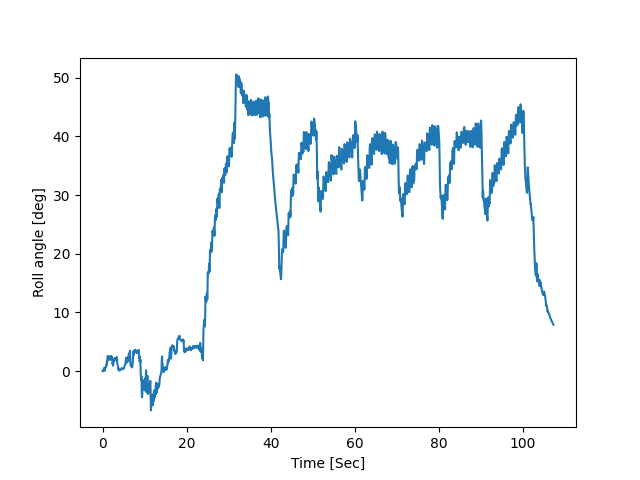
(image error) Size: 31 KiB 

|
54
euler_ekf.py
54
euler_ekf.py
@ -3,6 +3,7 @@ from numpy.linalg import inv
|
|||||||
import matplotlib.pyplot as plt
|
import matplotlib.pyplot as plt
|
||||||
from math import cos, sin, tan, asin, pi
|
from math import cos, sin, tan, asin, pi
|
||||||
import pandas as pd
|
import pandas as pd
|
||||||
|
from scipy.signal import butter, filtfilt
|
||||||
|
|
||||||
def get_data(i, data):
|
def get_data(i, data):
|
||||||
x = data[0][i] # (41500, 1)
|
x = data[0][i] # (41500, 1)
|
||||||
@ -87,23 +88,54 @@ def Euler_EKF(z, rates, dt):
|
|||||||
psi = x[2]
|
psi = x[2]
|
||||||
return phi, theta, psi
|
return phi, theta, psi
|
||||||
|
|
||||||
|
def butter_lowpass_filter(data, cutoff, fs, order):
|
||||||
|
nyq = (0.5 * fs) # Nyquist Frequency
|
||||||
|
normal_cutoff = cutoff / nyq
|
||||||
|
# Get the filter coefficients
|
||||||
|
b, a = butter(order, normal_cutoff, btype='low', analog=False)
|
||||||
|
y = filtfilt(b, a, data)
|
||||||
|
return y
|
||||||
|
|
||||||
def normalize_data_vector(data, division):
|
def normalize_data_vector(data, division):
|
||||||
return [i/division for i in list(data)]
|
return [i/division for i in list(data)]
|
||||||
|
|
||||||
H, Q, R = None, None, None
|
H, Q, R = None, None, None
|
||||||
x, P = None, None
|
x, P = None, None
|
||||||
firstRun = True
|
firstRun = True
|
||||||
|
|
||||||
division_param = 32768
|
division_param = 32768
|
||||||
|
|
||||||
|
# Filter requirements.
|
||||||
|
T = 5.0 # Sample Period
|
||||||
|
fs = 30.0 # sample rate, Hz
|
||||||
|
cutoff = 2 # desired cutoff frequency of the filter, Hz, slightly higher than actual 1.2 Hz
|
||||||
|
order = 2 # sin wave can be approx represented as quadratic
|
||||||
|
|
||||||
df = pd.read_csv('raw_data_6d.xls', sep='\t')
|
df = pd.read_csv('raw_data_6d.xls', sep='\t')
|
||||||
|
|
||||||
gyroX = normalize_data_vector(df['%GyroX'].values, division_param)
|
gyroX = df['%GyroX'].values
|
||||||
gyroY = normalize_data_vector(df['%GyroX'].values, division_param)
|
gyroY = df['GyroY'].values
|
||||||
gyroZ = normalize_data_vector(df['%GyroX'].values, division_param)
|
gyroZ = df['GyroZ'].values
|
||||||
|
|
||||||
acceX = normalize_data_vector(df['AcceX'].values, division_param)
|
acceX = df['AcceX'].values
|
||||||
acceY = normalize_data_vector(df['AcceY'].values, division_param)
|
acceY = df['AcceY'].values
|
||||||
acceZ = normalize_data_vector(df['AcceZ'].values, division_param)
|
acceZ = df['AcceZ'].values
|
||||||
|
|
||||||
|
gyroX = normalize_data_vector(gyroX, division_param)
|
||||||
|
gyroY = normalize_data_vector(gyroY, division_param)
|
||||||
|
gyroZ = normalize_data_vector(gyroZ, division_param)
|
||||||
|
|
||||||
|
acceX = normalize_data_vector(acceX, division_param)
|
||||||
|
acceY = normalize_data_vector(acceY, division_param)
|
||||||
|
acceZ = normalize_data_vector(acceZ, division_param)
|
||||||
|
|
||||||
|
# gyroX = butter_lowpass_filter(gyroX, cutoff, fs, order)
|
||||||
|
# gyroY = butter_lowpass_filter(gyroY, cutoff, fs, order)
|
||||||
|
# gyroZ = butter_lowpass_filter(gyroZ, cutoff, fs, order)
|
||||||
|
|
||||||
|
# acceX = butter_lowpass_filter(acceX, cutoff, fs, order)
|
||||||
|
# acceY = butter_lowpass_filter(acceY, cutoff, fs, order)
|
||||||
|
# acceZ = butter_lowpass_filter(acceZ, cutoff, fs, order)
|
||||||
|
|
||||||
gyro_data = [gyroX, gyroY, gyroZ]
|
gyro_data = [gyroX, gyroY, gyroZ]
|
||||||
acce_data = [acceX, acceY, acceZ]
|
acce_data = [acceX, acceY, acceZ]
|
||||||
@ -146,4 +178,12 @@ plt.subplot(133)
|
|||||||
plt.plot(t, PsiSaved)
|
plt.plot(t, PsiSaved)
|
||||||
plt.xlabel('Time [Sec]')
|
plt.xlabel('Time [Sec]')
|
||||||
plt.ylabel('Psi angle [deg]')
|
plt.ylabel('Psi angle [deg]')
|
||||||
'''
|
'''
|
||||||
|
|
||||||
|
n =int(T * fs)
|
||||||
|
# sin wave
|
||||||
|
sig = np.sin(1.2*2*np.pi*n)# Lets add some noise
|
||||||
|
noise = 1.5*np.cos(9*2*np.pi*n) + 0.5*np.sin(12.0*2*np.pi*n)
|
||||||
|
data = sig + noise
|
||||||
|
|
||||||
|
print(data)
|
||||||
|
|||||||
Loading…
Reference in New Issue
Block a user