uczenie-maszynowe/wyk/07_Metody_optymalizacji.ipynb

Uczenie maszynowe

7. Metody optymalizacji

7.1. Warianty metody gradientu prostego

• Batch gradient descent
• Stochastic gradient descent
• Mini-batch gradient descent

_Batch gradient descent

• Klasyczna wersja metody gradientu prostego
• Obliczamy gradient funkcji kosztu względem całego zbioru treningowego: $$ \theta := \theta - \alpha \cdot \nabla_\theta J(\theta) $$
• Dlatego może działać bardzo powoli
• Nie można dodawać nowych przykładów na bieżąco w trakcie trenowania modelu (_online learning)

_Stochastic gradient descent (SGD)

Algorytm

Powtórz określoną liczbę razy (liczba epok):

1. Randomizuj dane treningowe
2. Powtórz dla każdego przykładu $i = 1, 2, \ldots, m$: $$ \theta := \theta - \alpha \cdot \nabla_\theta , J ! \left( \theta, x^{(i)}, y^{(i)} \right) $$

Randomizacja danych to losowe potasowanie przykładów uczących (wraz z odpowiedziami).

SGD - zalety

• Dużo szybszy niż _batch gradient descent
• Można dodawać nowe przykłady na bieżąco w trakcie trenowania (_online learning)

SGD

• Częsta aktualizacja parametrów z dużą wariancją:

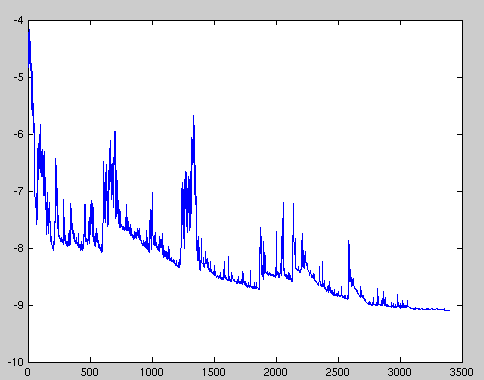
• Z jednej strony dzięki temu nie utyka w złych minimach lokalnych, ale z drugiej strony może „wyskoczyć” z dobrego minimum

_Mini-batch gradient descent

Algorytm

1. Ustal rozmiar "paczki/wsadu" (_batch) $b \leq m$.
2. Powtórz określoną liczbę razy (liczba epok):
3. Powtórz dla każdego batcha (czyli dla $i = 1, 1 + b, 1 + 2 b, \ldots$): $$ \theta := \theta - \alpha \cdot \nabla_\theta , J \left( \theta, x^{(i : i+b)}, y^{(i : i+b)} \right) $$

_Mini-batch gradient descent

• Kompromis między _batch gradient descent i SGD
• Stabilniejsza zbieżność dzięki redukcji wariancji aktualizacji parametrów
• Szybszy niż klasyczny _batch gradient descent
• Typowa wielkość batcha: między kilka a kilkaset przykładów
  • Im większy batch, tym bliżej do BGD; im mniejszy batch, tym bliżej do SGD
  • BGD i SGD można traktować jako odmiany MBGD dla $b = m$ i $b = 1$

# Mini-batch gradient descent - przykładowa implementacja

def MiniBatchSGD(h, fJ, fdJ, theta, X, y, 
        alpha=0.001, maxEpochs=1.0, batchSize=100, 
        logError=True):
    errorsX, errorsY = [], []
    
    m, n = X.shape
    start, end = 0, batchSize
    
    maxSteps = (m * float(maxEpochs)) / batchSize
    for i in range(int(maxSteps)):
        XBatch, yBatch =  X[start:end,:], y[start:end,:]

        theta = theta - alpha * fdJ(h, theta, XBatch, yBatch)
        
        if logError:
            errorsX.append(float(i*batchSize)/m)
            errorsY.append(fJ(h, theta, XBatch, yBatch).item())
        
        if start + batchSize < m:
            start += batchSize
        else:
            start = 0
        end = min(start + batchSize, m)
        
    return theta, (errorsX, errorsY)

Wady klasycznej metody gradientu prostego, czyli dlaczego potrzebujemy optymalizacji

• Trudno dobrać właściwą szybkość uczenia (_learning rate)
• Jedna ustalona wartość stałej uczenia się dla wszystkich parametrów
• Funkcja kosztu dla sieci neuronowych nie jest wypukła, więc uczenie może utknąć w złym minimum lokalnym lub punkcie siodłowym

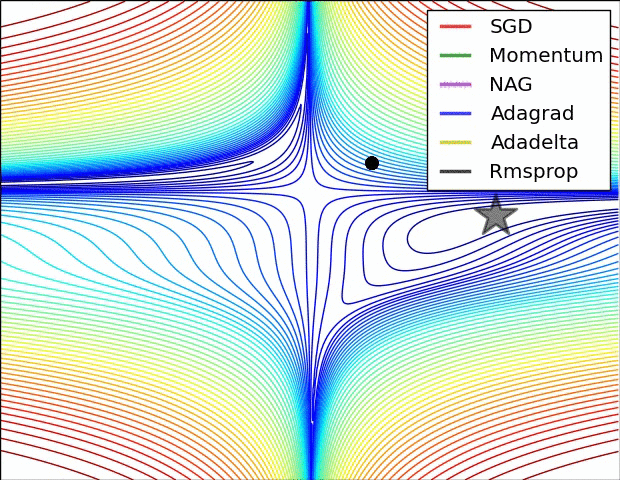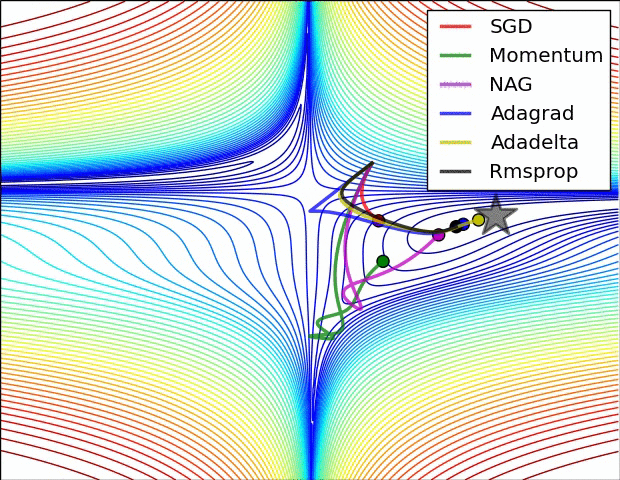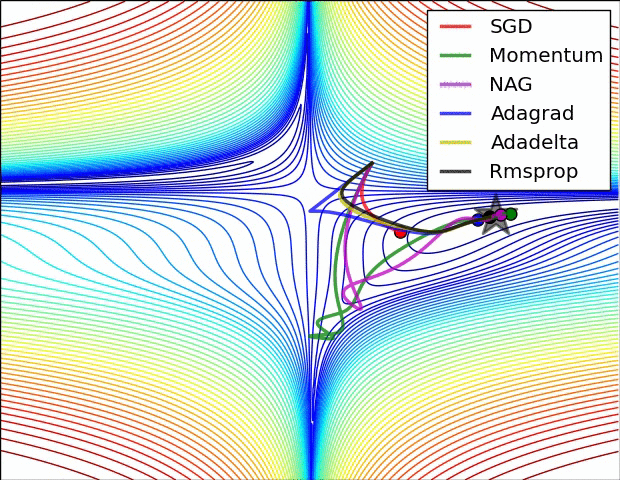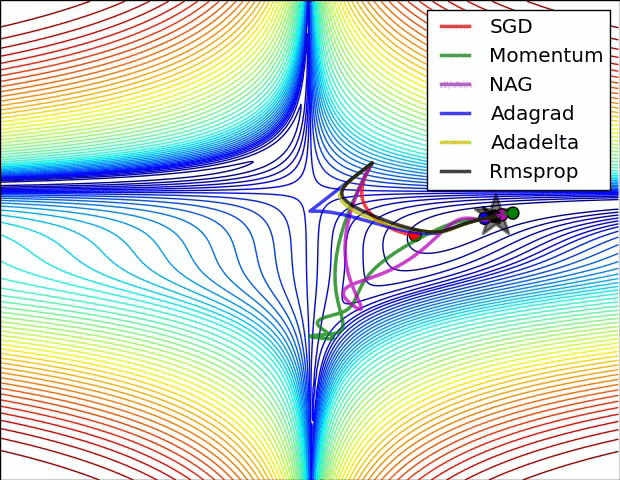
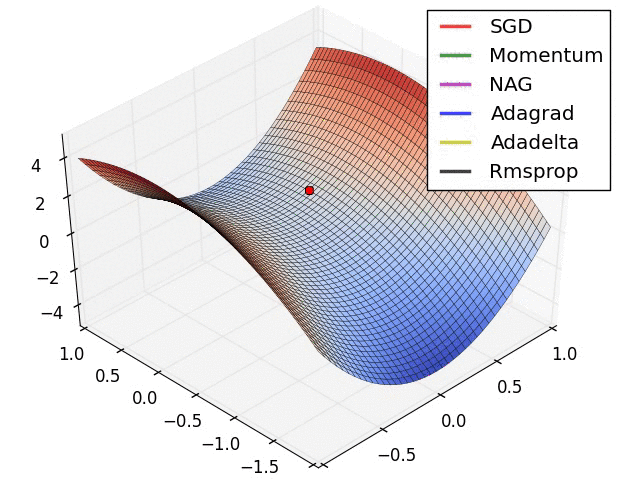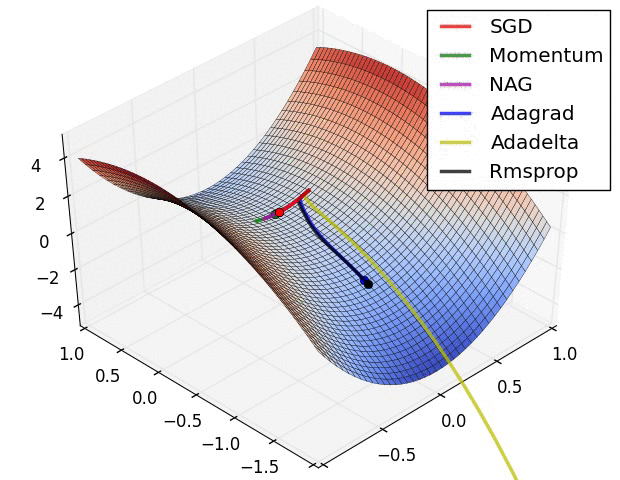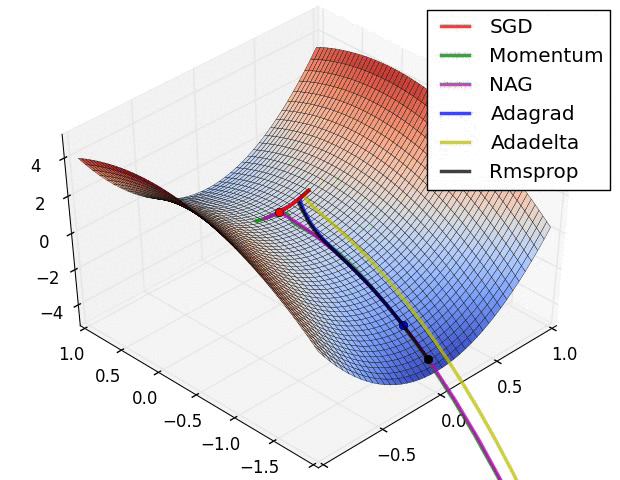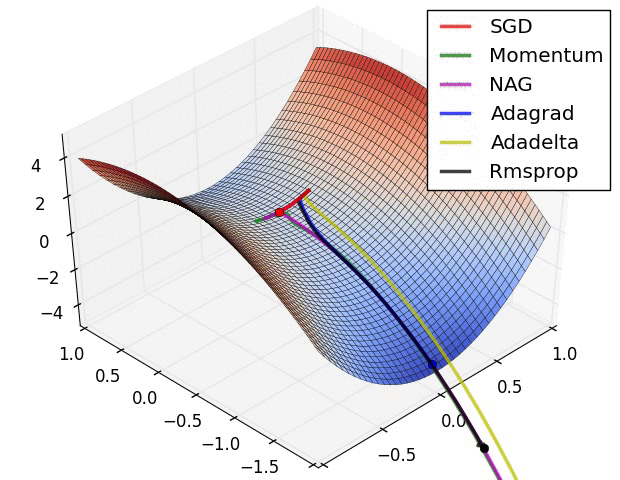
7.2. Algorytmy optymalizacji metody gradientu

• Momentum
• Nesterov Accelerated Gradient
• Adagrad
• Adadelta
• RMSprop
• Adam
• Nadam
• AMSGrad

Momentum

• SGD źle radzi sobie w „wąwozach” funkcji kosztu
• Momentum rozwiązuje ten problem przez dodanie współczynnika $\gamma$, który można trakować jako „pęd” spadającej piłki: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta) $$ $$ \theta := \theta - v_t $$

Przyspieszony gradient Nesterova (_Nesterov Accelerated Gradient, NAG)

• Momentum czasami powoduje niekontrolowane rozpędzanie się piłki, przez co staje się „mniej sterowna”
• Nesterov do piłki posiadającej pęd dodaje „hamulec”, który spowalnia piłkę przed wzniesieniem: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta - \gamma , v_{t-1}) $$ $$ \theta := \theta - v_t $$

Adagrad

• “Adaptive gradient”
• Adagrad dostosowuje współczynnik uczenia (_learning rate) do parametrów: zmniejsza go dla cech występujących częściej, a zwiększa dla występujących rzadziej:
• Świetny do trenowania na rzadkich (_sparse) zbiorach danych
• Wada: współczynnik uczenia może czasami gwałtownie maleć
• Wyniki badań pokazują, że często starannie dobrane $\alpha$ daje lepsze wyniki na zbiorze testowym

Adadelta i RMSprop

• Warianty algorytmu Adagrad, które radzą sobie z problemem gwałtownych zmian współczynnika uczenia

Adam

• “Adaptive moment estimation”
• Łączy zalety algorytmów RMSprop i Momentum
• Można go porównać do piłki mającej ciężar i opór
• Obecnie jeden z najpopularniejszych algorytmów optymalizacji

Nadam

• “Nesterov-accelerated adaptive moment estimation”
• Łączy zalety algorytmów Adam i Nesterov Accelerated Gradient

AMSGrad

• Wariant algorytmu Adam lepiej dostosowany do zadań takich jak rozpoznawanie obiektów czy tłumaczenie maszynowe

7.3. Metody zbiorcze

• Metody zbiorcze (_ensemble methods) używają połączonych sił wielu modeli uczenia maszynowego w celu uzyskania lepszej skuteczności niż mogłaby być osiągnięta przez każdy z tych modeli z osobna.

• Na metodę zbiorczą składa się:
  • dobór modeli
  • sposób agregacji wyników

• Warto zastosować randomizację, czyli przetasować zbiór uczący przed trenowaniem każdego modelu.

Uśrednianie prawdopodobieństw

Przykład

Mamy 3 modele, które dla klas $c=1, 2, 3, 4, 5$ zwróciły prawdopodobieństwa:

• $M_1$: [0.10, 0.40, 0.50, 0.00, 0.00]
• $M_2$: [0.10, 0.60, 0.20, 0.00, 0.10]
• $M_3$: [0.10, 0.30, 0.40, 0.00, 0.20]

Która klasa zostanie wybrana według średnich prawdopodobieństw dla każdej klasy?

Średnie prawdopodobieństwo: [0.10, 0.43, 0.36, 0.00, 0.10]

Została wybrana klasa $c = 2$

Głosowanie klas

Przykład

Mamy 3 modele, które dla klas $c=1, 2, 3, 4, 5$ zwróciły prawdopodobieństwa:

• $M_1$: [0.10, 0.40, 0.50, 0.00, 0.00]
• $M_2$: [0.10, 0.60, 0.20, 0.00, 0.10]
• $M_3$: [0.10, 0.30, 0.40, 0.00, 0.20]

Która klasa zostanie wybrana według głosowania?

Liczba głosów: [0, 1, 2, 0, 0]

Została wybrana klasa $c = 3$

Inne metody zbiorcze

• Bagging

• Boostng

• Stacking

  https://towardsdatascience.com/ensemble-methods-bagging-boosting-and-stacking-c9214a10a205