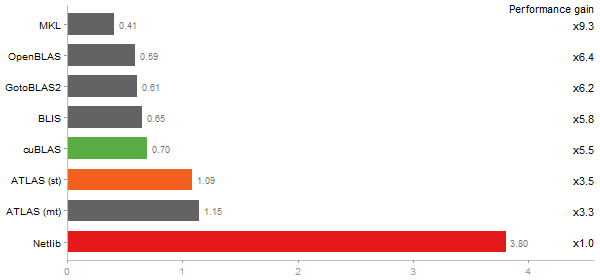
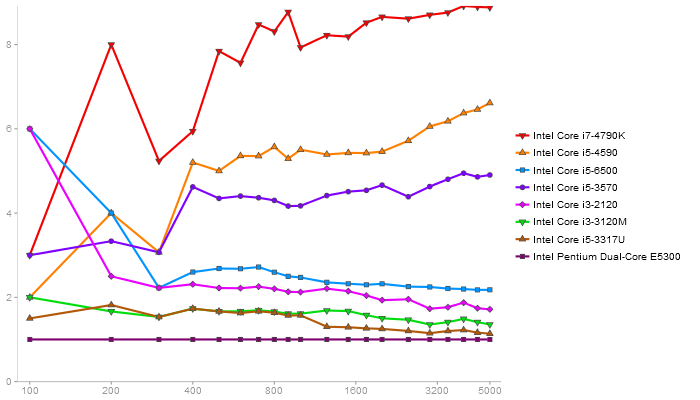
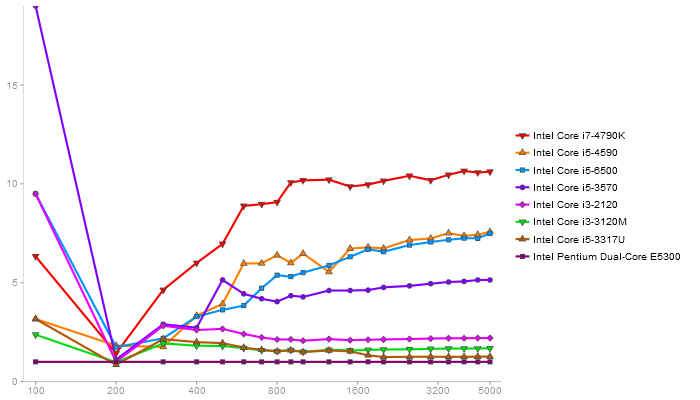
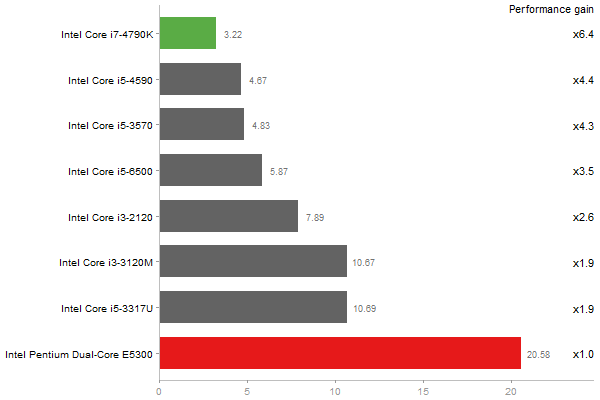
changed results view of gcbd benchmark to relative performance gain; changed reference CPU and GPU; target architecture detection fixes
42 KiB
BLAS libraries benchmarks
Andrzej Wójtowicz
Document generation date: 2016-07-14 17:20:41
This document presents timing results for BLAS (Basic Linear Algebra Subprograms) libraries in R on diverse CPUs and GPUs.
Changelog
- 2016-07-14: results: added Intel Core i5-6500; changed results view of gcbd benchmark to relative performance gain; changed reference CPU (Intel Pentium Dual-Core E5300) and GPU (NVIDIA GeForce GT 630M); code: fixed target architecture detection for Intel Core i5-6500-like CPUs in multi-threaded Atlas library; added info how to force target architecture in GotoBLAS2 and BLIS libraries.
Table of Contents
Configuration
OS: Debian Jessie, kernel 4.4
R software: Microsoft R Open (3.2.4)
Libraries:
| CPU (single-threaded) | CPU (multi-threaded) | GPU |
|---|---|---|
| Netlib (debian package, blas 1.2.20110419, lapack 3.5.0) | OpenBLAS (debian package, 0.2.12) | NVIDIA cuBLAS (NVBLAS 6.5 + Intel MKL) |
| ATLAS (debian package, 3.10.2) | ATLAS (dev branch, 3.11.38) | |
| GotoBLAS2 (Survive fork, 3.141) | ||
| Intel MKL (part of RevoMath package, 3.2.4) | ||
| BLIS (dev branch, 0.2.0+/17.05.2016) |
Hosts:
| No. | CPU | GPU |
|---|---|---|
| 1. | Intel Core i7-4790K (OC 4.5 GHz) | MSI GeForce GTX 980 Ti Lightning |
| 2. | Intel Core i5-4590 | NVIDIA GeForce GT 430 |
| 3. | Intel Core i5-4590 | NVIDIA GeForce GTX 750 Ti |
| 4. | Intel Core i5-6500 | - |
| 5. | Intel Core i5-3570 | - |
| 6. | Intel Core i3-2120 | - |
| 7. | Intel Core i3-3120M | - |
| 8. | Intel Core i5-3317U | NVIDIA GeForce GT 630M |
| 9. | Intel Pentium Dual-Core E5300 | - |
Benchmarks: R-benchmark-25, Revolution, Gcbd.
Results per host
Intel Core i7-4790K + MSI GeForce GTX 980 Ti Lightning
R-benchmark-25
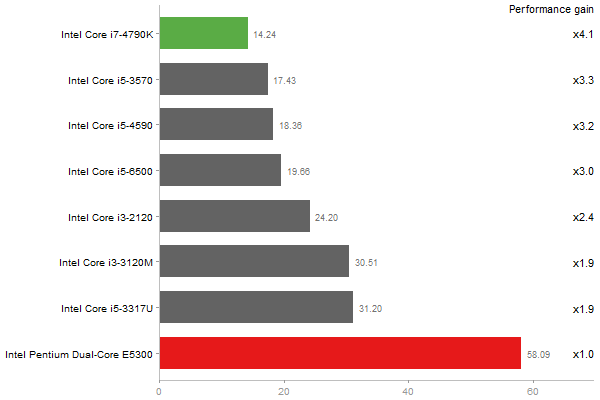
2800x2800 cross-product matrix
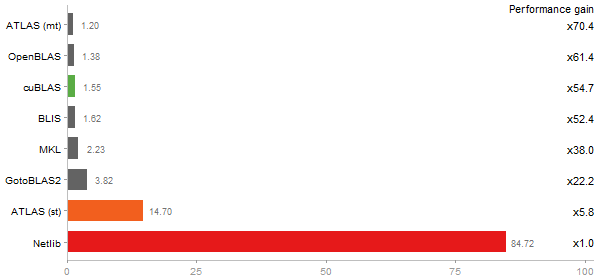
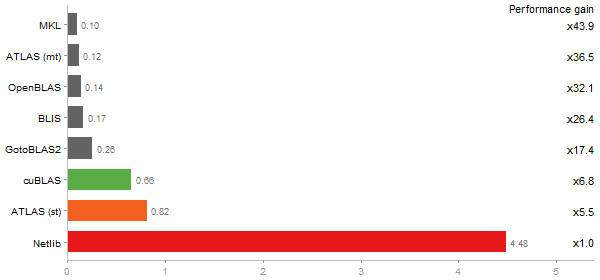
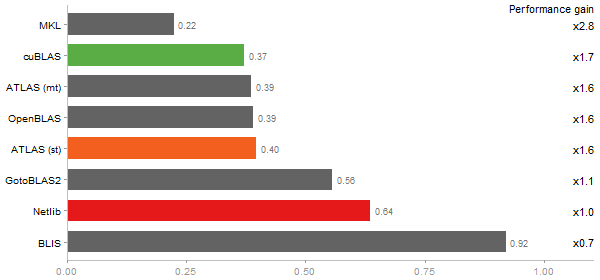
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
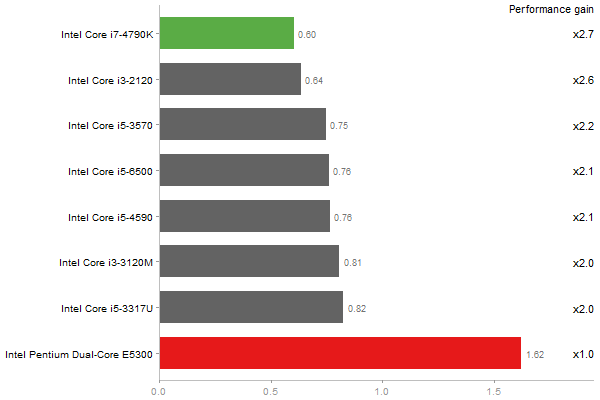
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
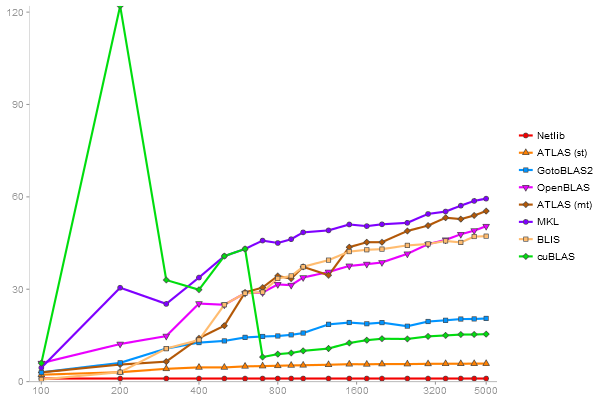
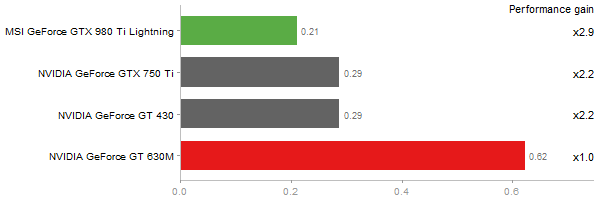
Matrix Multiply
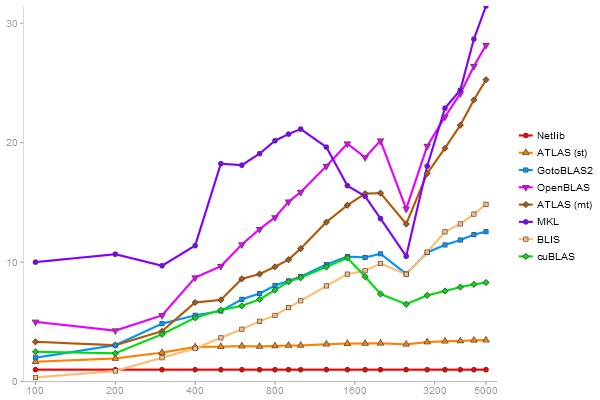
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
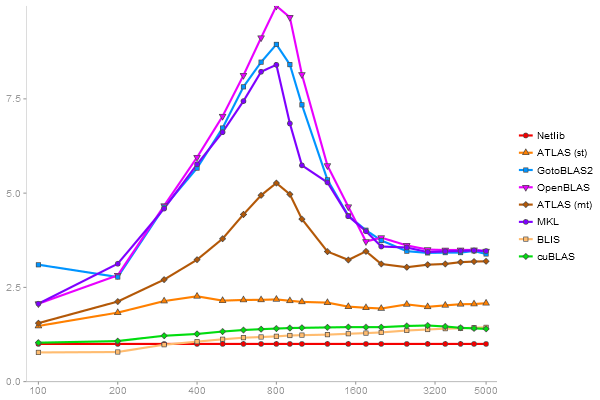
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i5-4590 + NVIDIA GeForce GT 430
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i5-4590 + NVIDIA GeForce GTX 750 Ti
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i5-6500
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i5-3570
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i3-2120
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i3-3120M
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Core i5-3317U + NVIDIA GeForce GT 630M
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Intel Pentium Dual-Core E5300
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
BLIS hangs in this test
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Netlib - from 50 to 5 runs - higher is better
Results per library
Netlib
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
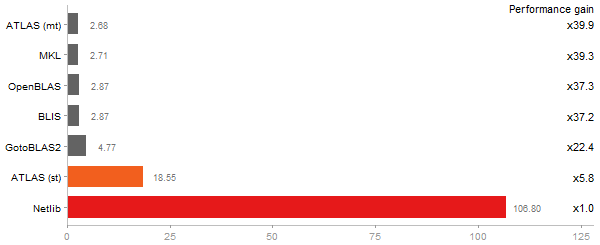
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
ATLAS (st)
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
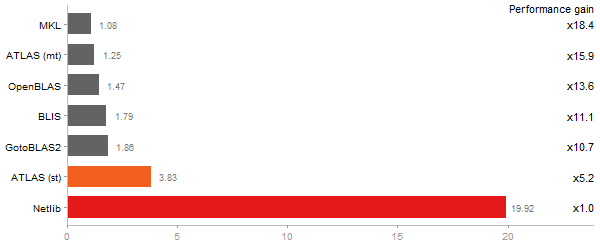
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
OpenBLAS
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
ATLAS (mt)
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
GotoBLAS2
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
MKL
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
BLIS
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Intel Pentium Dual-Core E5300 hangs in this test
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: Intel Pentium Dual-Core E5300 - from 50 to 5 runs - higher is better
cuBLAS
R-benchmark-25
2800x2800 cross-product matrix
Time in seconds - 10 runs - lower is better
Linear regr. over a 2000x2000 matrix
Time in seconds - 10 runs - lower is better
Eigenvalues of a 600x600 random matrix
Time in seconds - 10 runs - lower is better
Determinant of a 2500x2500 random matrix
Time in seconds - 10 runs - lower is better
Cholesky decomposition of a 3000x3000 matrix
Time in seconds - 10 runs - lower is better
Inverse of a 1600x1600 random matrix
Time in seconds - 10 runs - lower is better
Escoufier's method on a 45x45 matrix
Time in seconds - 10 runs - lower is better
Revolution benchmark
Matrix Multiply
Time in seconds - 10 runs - lower is better
Cholesky Factorization
Time in seconds - 10 runs - lower is better
Singular Value Deomposition
Time in seconds - 10 runs - lower is better
Principal Components Analysis
Time in seconds - 10 runs - lower is better
Linear Discriminant Analysis
Time in seconds - 10 runs - lower is better
Gcbd benchmark
Matrix Multiply
Performance gain regarding matrix size - reference: NVIDIA GeForce GT 630M - from 50 to 5 runs - higher is better
QR Decomposition
Performance gain regarding matrix size - reference: NVIDIA GeForce GT 630M - from 50 to 5 runs - higher is better
Singular Value Deomposition
Performance gain regarding matrix size - reference: NVIDIA GeForce GT 630M - from 50 to 5 runs - higher is better
Triangular Decomposition
Performance gain regarding matrix size - reference: NVIDIA GeForce GT 630M - from 50 to 5 runs - higher is better