4.7 KiB
Atencja
Sieci LSTM w roku 2017/2018 zostały wyparte przez nową, pod pewnymi względami prostszą, architekturę Transformer. Sieci Transformer oparte są zasadniczo na prostej idei atencji (_attention), pierwszy artykuł wprowadzający sieci Transformer nosił nawet tytuł Attention Is All You Need.
Intuicyjnie, atencja jest rodzajem uwagi, którą sieć może selektywnie kierować na wybrane miejsca (w modelowaniu języka: wybrane wyrazy).
Idea atencji jest jednak wcześniejsza, powstała jako ulepszenie sieci rekurencyjnych. My omówimy ją jednak na jeszcze prostszym przykładzie użycia w modelowaniu języka za pomocą hybrydy modelu bigramowego i modelu worka słów.
Prosty przykład zastosowania atencji
Wróćmy do naszego przykładu z Wykładu 8, w którym łączyliśmy $n$-gramowy model języka z workiem słów. Przyjmijmy bigramowy model języka ($n=2$), wówczas:
$$y = \operatorname{softmax}(C[E(w_{i-1}),A(w_1,\dots,w_{i-2})]),$$
gdzie $A$ była prostą agregacją (np. sumą albo średnią) embeddingów $E(w_1),\dots,E(w_{i-2})$. Aby wyjść z prostego nieuporządkowanego modelu worka słów, próbowaliśmy w prosty sposób uwzględnić pozycję wyrazów czy ich istotność (za pomocą odwrotnej częstości dokumentowej). Oba te sposoby niestety zupełnie nie uwzględniają kontekstu.
Innymi słowy, chcielibyśmy mieć sumę ważoną zanurzeń:
$$A(w_1,\dots,j) = \omega_1 E(w_1) + \dots \omega_j E(w_j) = \sum_{k=1}^j \omega_k E(w_k),$$
tak by $\omega_k$ w sposób bardziej zasadniczy zależały od lokalnego kontekstu, a nie tylko od pozycji $k$ czy słowa $w_k$. W naszym prostym przypadku jako kontekst możemy rozpatrywać słowo bezpośrednio poprzedzające odgadywane słowa (kontekstem jest $w_{i-1}$).
Wygodnie również przyjąć, że $\sum_{k=1}^j \omega_k = 1$, wówczas mamy do czynienia ze średnią ważoną.
Nieznormalizowane wagi atencji
Będziemy liczyć nieznormalizowane wagi atencji $\hat{\alpha}_{k,j}$. Określają one, jak bardzo słowo $w_j$ „zwraca uwagę” na poszczególne, inne słowa. Innymi słowy, wagi je opisują, jak bardzo słowo $w_k$ pasuje do naszego kontekstu, czyli słowa $w_j$.
Najprostszy sposób mierzenia dopasowania to po prostu iloczyn skalarn:
$$\hat{\alpha}_{k,j} = E(w_k)E(w_j),$$
można też alternatywnie złamać symetrię iloczynu skalarnego i wyliczać dopasowanie za pomocą prostej sieci feed-forward:
$$\hat{\alpha}_{k,j} = \vec{v}\operatorname{tanh}(W
W drugim przypadku pojawiają się dodatkowe wyuczalne paramatery: macierz $W_{\alpha}$, wektory $\vec{b_{\alpha}}$ i $\vec{v}$.
Normalizacja wag atencji
Jak już wspomniano, dobrze żeby wagi atencji sumowały się do 1. W tym celu możemy po prostu zastosować funkcję softmax:
$$\alpha_{k,j} = \operatorname{softmax}([\hat{\alpha}_{1,j},\dots,\hat{\alpha}{j-1,j}]).$$
Zauważmy jednak, że otrzymanego z funkcji softmax wektora $[\alpha_{1,j},\dots,\alpha_{j-1,j}]$ tym razem nie interpretujemy jako rozkład prawdopodobieństwa. Jest to raczej rozkład uwagi, atencji słowa $w_j$ względem innych słów.
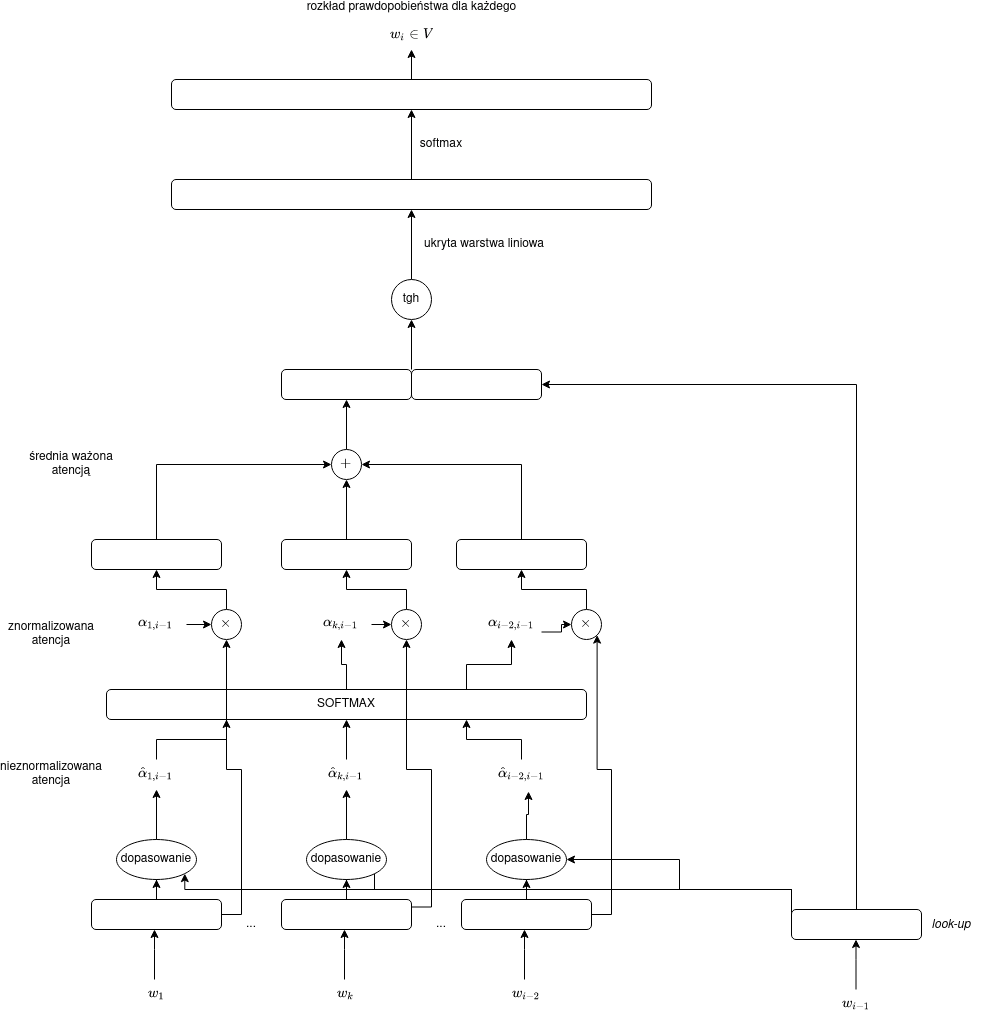
Użycie wag atencji w prostym neuronowym modelu języka
Teraz jako wagi $\omega$ w naszym modelu języka możemy przyjąć:
$$\omega_k = \alpha_{k,i-1}.$$
Oznacza to, że z naszego worka będziemy „wyjmowali” słowa w sposób selektywny w zależności od wyrazu, który bezpośrednio poprzedza słowo odgadywane.