6.9 KiB
- Neuronowy n-gramowy model języka
Neuronowy n-gramowy model języka
Omówiony w poprzedniej części neuronowy bigramowy model języka warunkuje kolejny wyraz jedynie względem bezpośrednio poprzedzającego — jak w każdym bigramowym modelu przyjmujemy założenie, że $w_i$ zależy tylko od $w_{i-1}$. Rzecz jasna jest to bardzo duże ograniczenie, w rzeczywistości bardzo często prawdopodobieństwo kolejnego wyrazu zależy od wyrazu dwie, trzy, cztery itd. pozycje wstecz czy w ogólności od wszystkich wyrazów poprzedzających (bez względu na ich pozycje).
Pytanie: Wskaż zależności o zasięgu większym niż 1 wyraz w zdaniu /Zatopieni w kłębach dymu cygar i pochyleni nad butelkami z ciemnego szkła obywatele tej dzielnicy, jedni zakładali się o wygranę lub przegranę Anglii, drudzy o bankructwo Wokulskiego; jedni nazywali geniuszem Bismarcka, drudzy — awanturnikiem Wokulskiego; jedni krytykowali postępowanie prezydenta MacMahona, inni twierdzili, że Wokulski jest zdecydowanym wariatem, jeżeli nie czymś gorszym…/
Trigramowy neuronowy model języka
Spróbujmy najpierw rozszerzyć nasz model na trigramy, to znaczy będziemy przewidywać słowo $w_i$ na podstawie słów $w_{i-2}$ i $w_{i-1}$.
Najprostsze rozwiązanie polegałoby na zanurzeniu pary $(w_{i-2}, w_{i-1})$ w całości i postępowaniu jak w przypadku modelu bigramowego. Byłoby to jednak zupełnie niepraktyczne, jako że:
- liczba zanurzeń do wyuczenia byłaby olbrzymia ($|V|^2$ — byłoby to ewentualnie akceptowalne dla modeli operujących na krótszych jednostkach niż słowa, np. na znakach),
- w szczególności zanurzenia dla par $(v, u)$, $(u, v)$, $(u, u)$ i $(v, v)$ nie miałyby ze sobą nic wspólnego.
Konketanacja zanurzeń
Właściwsze rozwiązanie polega na zanurzeniu dalej pojedynczych słów i następnie ich konkatenowaniu.
Przypomnijmy, że konkatenacja wektorów $\vec{x_1}$ i $\vec{x_2}$ to wektor o rozmiarze $|\vec{x_1}| + |\vec{x_2}|$ powstały ze „sklejania” wektorów $\vec{x_1}$ i $\vec{x_2}$. Konkatenację wektorów $\vec{x_1}$ i $\vec{x_2}$ będziemy oznaczać za pomocą $[\vec{x_1}, \vec{x_2}]$.
Przykład: jeśli $\vec{x_1} = [-1, 2, 0]$ i $\vec{x_2} = [3, -3]$, wówczas $[\vec{x_1}, \vec{x_2}] = [-1, 2, 0, 3, -3]$
Oznacza to, że nasza macierz „kontekstowa” $C$ powinna mieć w modelu trigramowym rozmiar nie $|V| \times m$, lecz $|V| \times (m+m)$ = $|V| \times 2m$ i wyjście będzie zdefiniowane za pomocą wzoru:
$$\vec{y} = \operatorname{softmax}(C[E(w_{i-2}),E(w_{i-1})]),$$
co można przedstawić za pomocą następującego schematu:
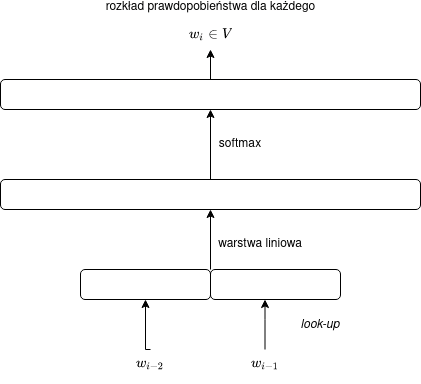
Rozbicie macierzy $C$
Zamiast mnożyć macierz $C$ przez konkatenację dwóch wektorów, można rozbić macierz $C$ na dwie, powiedzmy $C_{-2}$ i $C_{-1}$, przemnażać je osobno przez odpowiadające im wektory i następnie dodać macierze, tak aby:
$$C[E(w_{i-2}),E(w_{i-1})] = C_{-2}E(w_{i-2}) + C_{-1}E(w_{i-1}).$$
Macierze $C_{-2}$ i $C_{-1}$ będą miały rozmiar $|V| \times m$.
Przy tym podejściu możemy powiedzieć, że ostatni i przedostatni wyraz mają swoje osobne macierze o potencjalnie różnych wagach — co ma sens, jako że na inne aspekty zwracamy uwagę przewidując kolejne słowo na podstawie wyrazu bezpośrednio poprzedzającego, a na inne — na podstawie słowa występującego dwie pozycje wcześniej.
Uogólnienie na $n$-gramowy model języka dla dowolnego $n$
Łatwo uogólnić opisany wyżej trigramowy model języka dla dowolnego $n$. Uogólniony model można przedstawić za pomocą wzoru:
$$\vec{y} = \operatorname{softmax}(C[E(w_{i-n+1}),\dots,E(w_{i-1})]),$$
gdzie macierz $C$ ma rozmiar $|V| \times nm$ lub za pomocą wzoru:
$$\vec{y} = \operatorname{softmax}(C_{-(n-1)}E(w_{i-n+1}) + \dots + C_{-1}E(w_{i-1}),$$
gdzie macierze $C_{-(n-1)}$, …, $C_{-1}$ mają rozmiary $|V| \times m$.
Por. diagram:
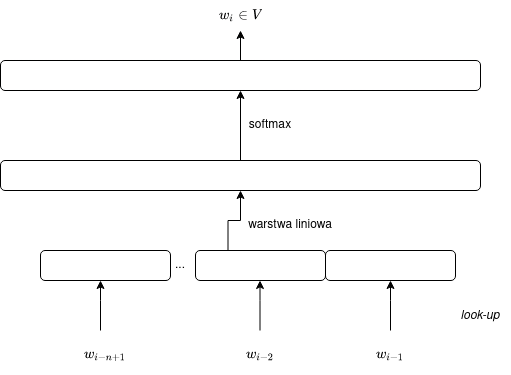
Dodanie kolejnej warstwy
W wypadku trigramowego czy — ogólniej — n-gramowego modelu języka dla $n \geq 3$ warto dodać kolejną (ukrytą) warstwę, na którą będziemy rzutować skonkatenowane embeddingi, zanim zrzutujemy je do długiego wektora prawdopodobieństw.
Zakładamy, że warstwa ukryta zawiera $h$ neuronów. Wartość $h$ powinna być mniejsza niż $nm$ (a może nawet od $m$).
Pytanie: Dlaczego wartość $h > nm$ nie jest racjonalnym wyborem?
Pytanie: Dlaczego dodanie kolejnej warstwy nie ma sensu dla modelu bigramowego?
Funkcja aktywacji
Aby warstwa ukryta wnosiła coś nowego, na wyjściu z tej funkcji musimy (dlaczego?) zastosować nieliniową funkcji aktywacji. Zazwyczaj jako funkcji aktywacji w sieciach neuronowych używa się funkcji ReLU albo funkcji sigmoidalnej. W prostych neuronowych modelach języka sprawdza się też tangens hiperboliczny (tgh, w literaturze anglojęzycznej tanh):
$$\operatorname{tgh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}.$$
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
x = torch.linspace(-5,5,100)
plt.xlabel("x")
plt.ylabel("y")
a = torch.Tensor(x.size()[0]).fill_(2.)
m = torch.stack([x, a])
plt.plot(x, nn.functional.tanh(m)[0])
fname = '10_Neuronowy_ngramowy_model/tanh.png'
plt.savefig(fname)
fname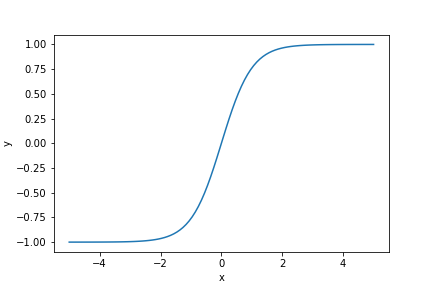
Tangens hiperboliczny zastosowany dla wektora
Tangens hiperboliczny wektora będzie po prostu wektorem tangensów hiperbolicznych poszczególnych wartości.
import torch
import torch.nn as nn
v = torch.Tensor([-100, -2.0, 0.0, 0.5, 1000.0])
nn.functional.tanh(v)Wzór i schemat dwuwarstwowego n-gramowego neuronowego modelu języka
Dwuwarstwowy model języka będzie określony następującym wzorem:
$$\vec{y} = \operatorname{softmax}(C\operatorname{tgh}(W[E(w_{i-n+1}),\dots,E(w_{i-1})])),$$
gdzie:
- $W$ jest wyuczalną macierzą wag o rozmiarze $h \times nm$,
- $C$ będzie macierzą o rozmiarze $|V| \times h$.
Zmodyfikowaną sieć można przedstawić za pomocą następującego schematu:
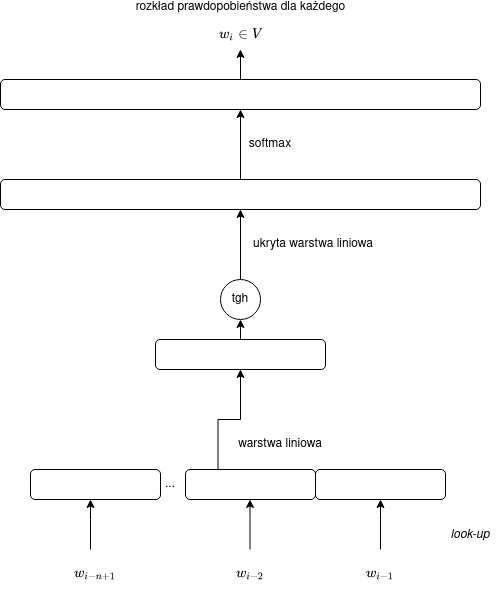
Liczba wag w modelu dwuwarstwowym
Na wagi w modelu dwuwarstwowym składają się:
- zanurzenia: $m|V|$,
- wagi warstwy ukrytej: $hnm$,
- wagi warstwy wyjściowej: $|V|h$,
a zatem łącznie:
$$m|V| + hnm + |V|h$$
Jeśli $h \approx m$ (co jest realistyczną opcją), wówczas otrzymamy oszacowanie:
$$O(m|V| + nm^2).$$
Zauważmy, że względem $n$ oznacza to bardzo korzystną złożoność $O(n)$! Oznacza to, że nasz model może działać dla dużo większych wartości $n$ niż tradycyjny, statystyczny n-gramowy model języka (dla którego wartości $n > 5$ zazwyczaj nie mają sensu).