5.8 KiB
Model języka oparty na rekurencyjnej sieci neuronowej
Podejście rekurencyjne
Na poprzednim wykładzie rozpatrywaliśmy różne funkcje $A(w_1,\dots,w_{i-1})$, dzięki którym możliwe było „skompresowanie” ciągu słów (a właściwie ich zanurzeń) dowolnej długości w wektor o stałej długości.
Funkcję $A$ moglibyśmy zdefiniować w inny sposób, w sposób rekurencyjny.
Otóż moglibyśmy zdekomponować funkcję $A$ do
- pewnego stanu początkowego $\vec{s^0} \in \mathcal{R}^p$,
- pewnej funkcji rekurencyjnej $R : \mathcal{R}^p \times \mathcal{R}^m \rightarrow \mathcal{R}^p$.
Wówczas funkcję $A$ można będzie zdefiniować rekurencyjnie jako:
$$A(w_1,\dots,w_t) = R(A(w_1,\dots,w_{t-1}), E(w_t)),$$
przy czym dla ciągu pustego:
$$A(\epsilon) = \vec{s^0}$$
Przypomnijmy, że $m$ to rozmiar zanurzenia (embeddingu). Z kolei $p$ to rozmiar wektora stanu (często $p=m$, ale nie jest to konieczne).
Przy takim podejściu rekurencyjnym wprowadzamy niejako „strzałkę czasu”, możemy mówić o przetwarzaniu krok po kroku.
W wypadku modelowania języka możemy końcowy wektor stanu zrzutować do wektora o rozmiarze słownika i zastosować softmax:
$$\vec{y} = \operatorname{softmax}(CA(w_1,\dots,w_{i-1})),$$
gdzie $C$ jest wyuczalną macierzą o rozmiarze $|V| \times p$.
Worek słów zdefiniowany rekurencyjnie
Nietrudno zdefiniować model „worka słów” w taki rekurencyjny sposób:
- $p=m$,
- $\vec{s^0} = [0,\dots,0]$,
- $R(\vec{s}, \vec{x}) = \vec{s} + \vec{x}.$
Dodawanie (również wektorowe) jest operacją przemienną i łączną, więc to rekurencyjne spojrzenie niewiele tu wnosi. Można jednak zastosować funkcję $R$, która nie jest przemienna — w ten sposób wyjdziemy poza nieuporządkowany worek słów.
Związek z programowaniem funkcyjnym
Zauważmy, że stosowane tutaj podejście jest tożsame z zastosowaniem funkcji typu fold
w językach funkcyjnych:
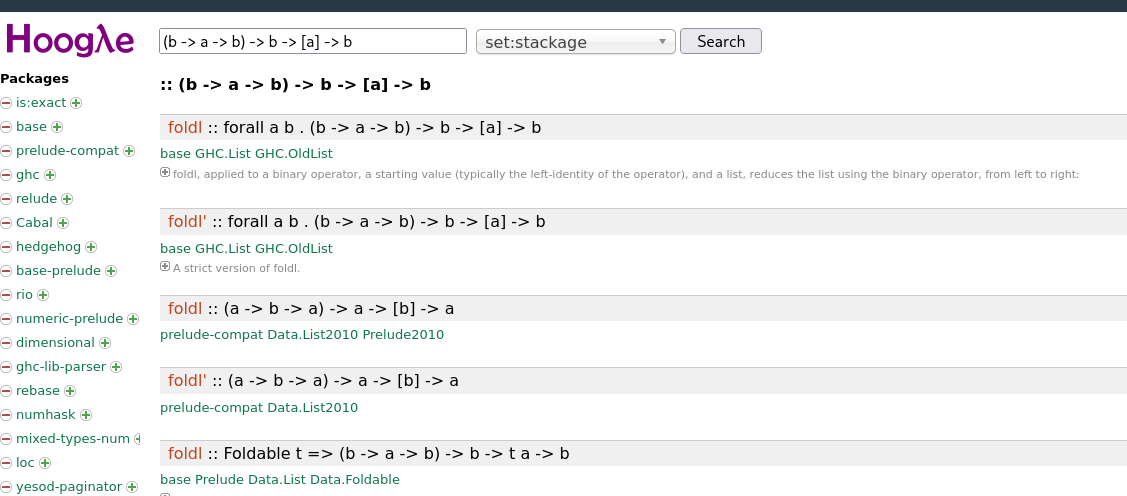
W Pythonie odpowiednik fold jest funkcja reduce z pakietu functools:
from functools import reduce
def product(ns):
return reduce(lambda a, b: a * b, ns, 1)
product([2, 3, 1, 3])18
Sieci rekurencyjne
W jaki sposób „złamać” przemienność i wprowadzić porządek? Jedną z najprostszych operacji nieprzemiennych jest konkatenacja — możemy dokonać konkatenacji wektora stanu i bieżącego stanu, a następnie zastosować jakąś prostą operację (na wyjściu musimy mieć wektor o rozmiarze $p$, nie $p + m$!), dobrze przy okazji „złamać” też liniowość operacji. Możemy po prostu zastosować rzutowanie (mnożenie przez macierz) i jakąś prostą funkcję aktywacji (na przykład sigmoidę):
$$R(\vec{s}, \vec{e}) = \sigma(W[\vec{s},\vec{e}] + \vec{b}).$$
Dodatkowo jeszcze wprowadziliśmy wektor obciążeń $\vec{b}, a zatem wyuczalne wagi to:
- macierz $W \in \mathcal{R}^p \times \mathcal{R}^{p+m}$,
- wektor obciążń $b \in \mathcal{R}^p$.
Olbrzymią zaletą sieci rekurencyjnych jest fakt, że liczba wag nie zależy od rozmiaru wejścia!
Zwykła sieć rekurencyjna
Wyżej zdefiniową sieć nazywamy „zwykłą” siecią rekurencyjną (Vanilla RNN).
Uwaga: przez RNN czasami rozumie się taką „zwykłą” sieć rekurencyjną, a czasami szerszą klasę sieci rekurencyjnych obejmujących również sieci GRU czy LSTM (zob. poniżej).
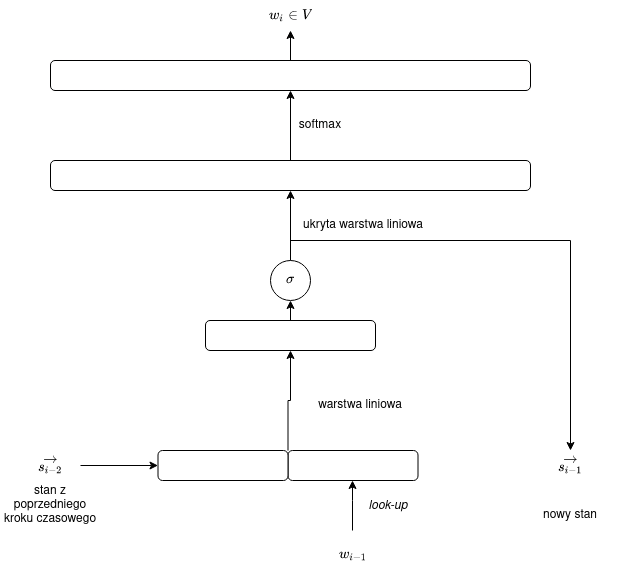
Uwaga: powyższy schemat nie obejmuje już „całego” działania sieci, tylko pojedynczy krok czasowy.
Praktyczna niestosowalność prostych sieci RNN
Niestety w praktyce proste sieci RNN sprawiają duże trudności jeśli chodzi o propagację wsteczną — pojawia się zjawisko zanikającego (rzadziej: eksplodującego) gradientu. Dlatego zaproponowano różne modyfikacje sieci RNN. Zacznijmy od omówienia stosunkowo prostej sieci GRU.
Sieć GRU
GRU (Gated Recurrent Unit) to sieć z dwiema bramkami (gates):
- bramką resetu (reset gate) $\Gamma_\gamma \in \mathcal{R}^p$ — która określa, w jakim stopniu sieć ma pamiętać albo zapominać stan z poprzedniego kroku,
- bramką aktualizacji (update gate) $\Gamma_u \in \mathcal{R}^p$ — która określa wpływ bieżącego wyrazu na zmianę stanu.
Tak więc w skrajnym przypadku:
- jeśli $\Gamma_\gamma = [0,\dots,0]$, sieć całkowicie zapomina informację płynącą z poprzednich wyrazów,
- jeśli $\Gamma_\update = [0,\dots,0]$, sieć nie bierze pod uwagę bieżącego wyrazu.
Zauważmy, że bramki mogą selektywnie, na każdej pozycji wektora stanu, sterować przepływem informacji. Na przykład $Gamma_\gamma = [0,1,\dots,1]$ oznacza, że pierwsza pozycja wektora stanu jest zapominana, a pozostałe — wnoszą wkład w całości.
Wzory
Najpierw zdefiniujmy pośredni stan $\vec{\xi} \in \mathcal{R}^p$:
$$\vec{\xi_t} = \operatorname{tanh}(W_{\xi}[\Gamma_\gamma \bullet c_{t-1}, E(w_t)] + b_{\xi}),$$
gdzie $\bullet$ oznacza iloczyn Hadamarda (nie iloczyn skalarny!) dwóch wektorów:
$$[x_1,\dots,x_n] \bullet [y_1,\dots,y_n] = [x_1 y_1,\dots,x_n y_n].$$
Obliczanie $$\vec{\xi_t}$$ bardzo przypomina zwykłą sieć rekurencyjną, jedyna różnica polega na tym, że za pomocą bramki $\Gamma_\gamma$ modulujemy wpływ poprzedniego stanu.
Ostateczna wartość stanu jest średnią ważoną poprzedniego stanu i bieżącego stanu pośredniego:
$$\vec{c_t} = \Gamma_u \bullet \vec{\xi_t} + (1 - \Gamma_u) \bullet \vec{c_{t-1}}.$$
Skąd się biorą bramki $\Gamma_\gamma$ i $\Gamma_u$? Również z poprzedniego stanu i z biężacego wyrazu.
$$\Gamma_\gamma = \sigma(W_\gamma[\vec{c_{t-1}},E(w_t)] + b_\gamma),$$
$$\Gamma_u = \sigma(W_u[\vec{c_{t-1}},E(w_t)] + b_u),$$