aitech-eks-pub-22/cw/07_regresja_liniowa.ipynb

Ekstrakcja informacji

7. Regresja liniowa [ćwiczenia]

Jakub Pokrywka (2021)

Regresja liniowa

import bibliotek

import pandas as pd
import numpy as np
from pathlib import Path
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
plt.rcParams['figure.figsize'] = [10, 5]

Zbiór

https://git.wmi.amu.edu.pl/kubapok/mieszkania2-below1m-public

ładowanie zbioru train

DATA_DIR = Path('/home/kuba/Syncthing/przedmioty/2020-02/ISI/zajecia7_regresja_liniowa/mieszkania2')

with open(DATA_DIR / 'names') as f_names:
    names = f_names.read().rstrip('\n').split('\t')

mieszkania_train = pd.read_csv(DATA_DIR/'train/in.tsv', sep ='\t', names=names)

mieszkania_train.head()

	isNew	rooms	floor	location	sqrMetres
0	False	3	1	Centrum	78
1	False	3	2	Sołacz	62
2	False	3	0	Sołacz	15
3	False	4	0	Sołacz	14
4	False	3	0	Sołacz	15

with open(DATA_DIR/'train'/'expected.tsv','r') as train_exp_f:
    Y_train = np.array([float(x.rstrip('\n')) for x in train_exp_f.readlines()])

Y_train

array([476118., 459531., 411557., ..., 320000., 364000., 209000.])

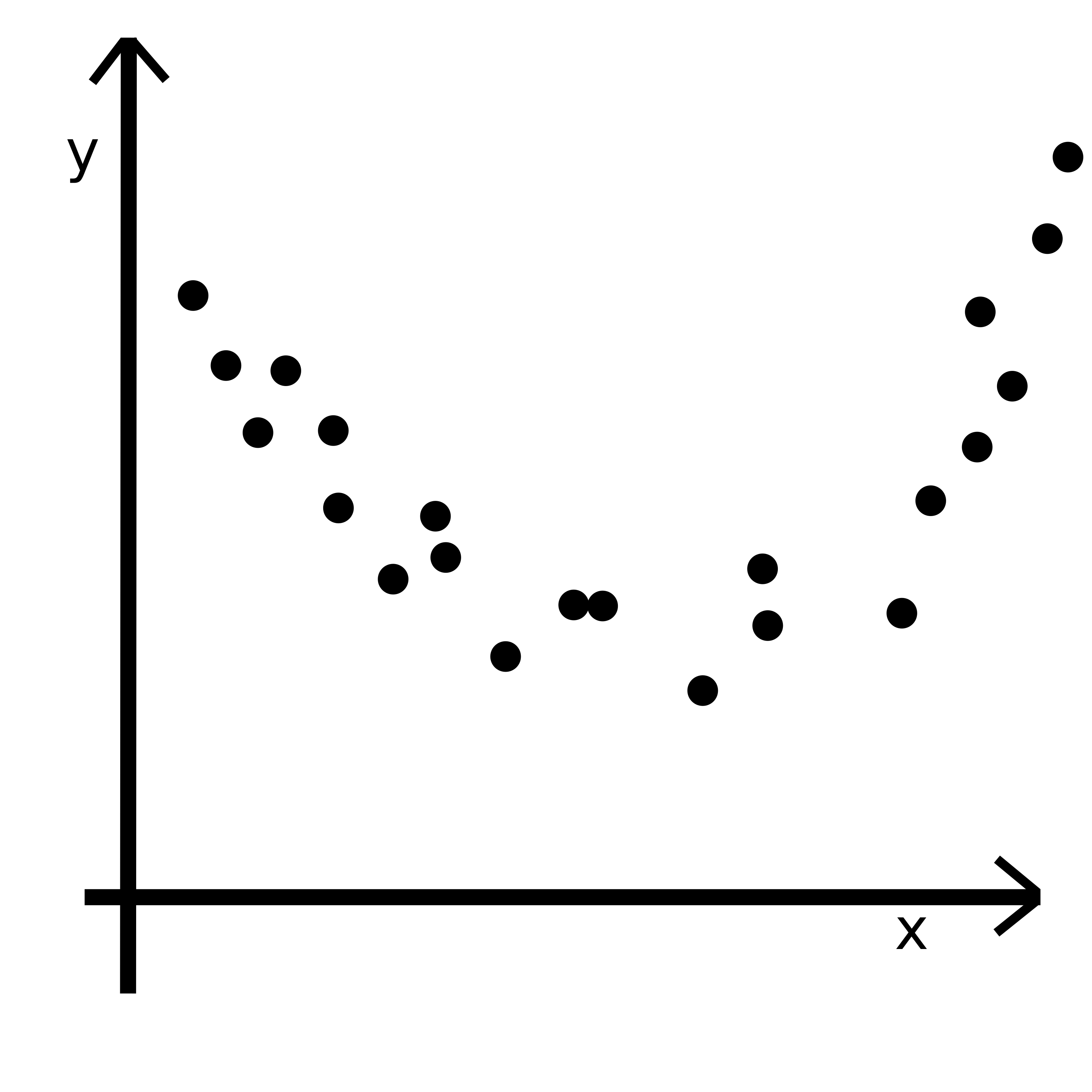
mieszkania_train['price'] = Y_train

X_train = mieszkania_train['sqrMetres'].to_numpy()

Wizualizacja danych

mieszkania_train

	isNew	rooms	floor	location	sqrMetres	price
0	False	3	1	Centrum	78	476118.0
1	False	3	2	Sołacz	62	459531.0
2	False	3	0	Sołacz	15	411557.0
3	False	4	0	Sołacz	14	496416.0
4	False	3	0	Sołacz	15	406032.0
...	...	...	...	...	...	...
1652	True	2	0	Grunwald	51	299000.0
1653	True	2	2	Centrum	53	339000.0
1654	True	3	4	Stare	65	320000.0
1655	True	3	1	Nowe	67	364000.0
1656	True	3	3	Grunwald	50	209000.0

1657 rows × 6 columns

sns.scatterplot(x='sqrMetres',y='price', data = mieszkania_train, linewidth = 0, s = 5)

<AxesSubplot:xlabel='sqrMetres', ylabel='price'>

Pytanie- Jaki jest baseline naszego systemu?

Czym jest regresja liniowa?- przypadek jednowymiarowym

wzór na regresję w przypadku jednowymiarowym?

$Y = a*X_1 + b$

$Y = w_1 * X_1 + w_0$

Zadanie - napisać funkcję predict_score(sqr_metres) która zwraca cenę mieszkania zgodnie z modelem regresji liniowej ( 5 minut)

Należy samemu wymyślić współczynniki modelu

def predict_price(sqr_metres):
    pass

predict_price(20)

predict_price(40)

predict_price(55)

predict_price(0)

Y_train_predicted = predict_price(X_train)

Mierzenie błędu

Zadanie - napisać funkcję, która liczy błąd średniowadratowy na całym zbiorze (7 minut)

rmse(Y_true, Y_predicted)

def rmse(Y_true, Y_predicted):
    pass 

rmse(np.array([300_000, 250_000]), np.array([300_000, 250_000]))

rmse(np.array([305_000, 250_000]) ,np.array([300_000, 350_000]) )

rmse(np.array([300_000, 250_000]), np.array([330_000, 360_000]))

Zadanie - za pomocą rmse policzyć błąd dla baseline (3 minuty)

Zadanie - za pomocą rmse policzyc błąd dla predykcji (2 minuty)

Na jakim zbiorze najlepiej sprawdzać wyniki?

mieszkania_dev = pd.read_csv(DATA_DIR/'dev-0'/'in.tsv', sep = '\t', names = names)

with open(DATA_DIR/'dev-0'/'expected.tsv','r') as dev_exp_f:
    Y_dev = np.array([float(x.rstrip('\n')) for x in dev_exp_f.readlines()])

mieszkania_dev['price'] = Y_dev

X_dev = mieszkania_dev['sqrMetres'].to_numpy()

sns.scatterplot(x='sqrMetres',y='price', data = mieszkania_dev, linewidth = 0, s = 5)

<AxesSubplot:xlabel='sqrMetres', ylabel='price'>

Zadanie - policzyć rmse dla predykcji ze zbioru deweloperskiego modelu baseline i naszego modelu regresji liniowej

Przypadek wielowymiarowy

sns.scatterplot(x='floor',y='price', data = mieszkania_train, linewidth = 0, s = 5)

<AxesSubplot:xlabel='floor', ylabel='price'>

$Y = w_1 * X_1 + w_2 * X_1 + w_3 * X_3 + w_0$

Zadanie. Napisać analogiczną funkcję predict_price(sqr_metres, floor), policzyć rmse dla takiego modelu ( 7 minut)

jak dobrać najlepsze parametry?

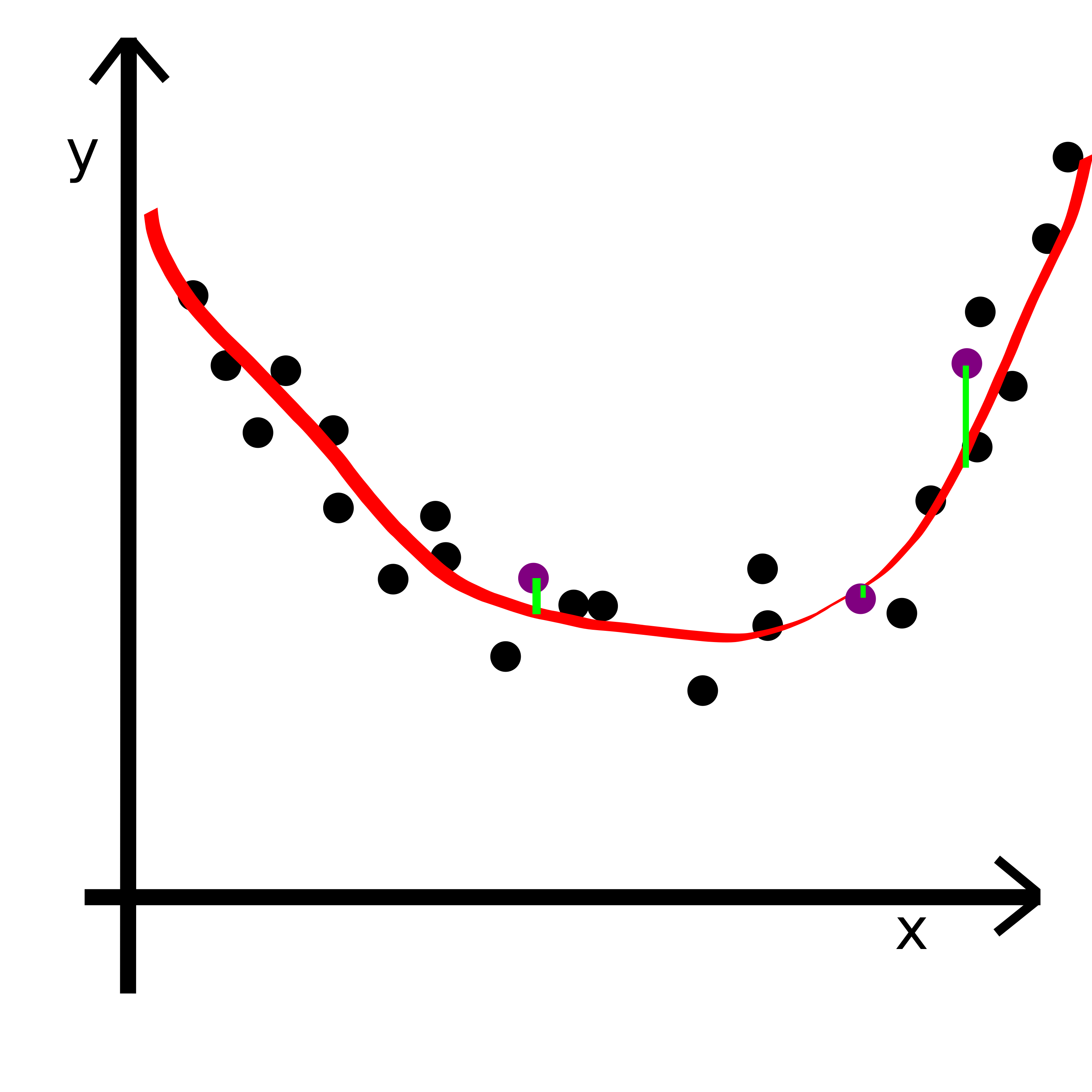
sns.lmplot(x='sqrMetres',y='price', data = mieszkania_train)

<seaborn.axisgrid.FacetGrid at 0x7fbaa0c46760>

https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html

lm_model = LinearRegression()

lm_model.fit(mieszkania_train[['isNew','rooms', 'floor', 'sqrMetres']], Y_train)

LinearRegression()

Y_train_predicted = lm_model.predict(mieszkania_train[['isNew','rooms', 'floor', 'sqrMetres']])

rmse(Y_train, Y_train_predicted)

Y_dev_predicted = lm_model.predict(mieszkania_dev[['isNew','rooms', 'floor', 'sqrMetres']])

rmse(Y_dev, Y_dev_predicted)

lm_model.predict(np.array(([[0, 4, 3, 70]])))

array([469449.27836213])

lm_model.predict(np.array(([[0, 4, 3, 60]])))

array([455982.54297977])

lm_model.coef_

array([ 4522.65059749, 73763.4125433 ,   -78.83243119,  1346.67353824])

lm_model.intercept_

80364.97780599026

0 * 4522.65059749 + 4* 73763.4125433 + 3 * (-78.83243119) + 60 * 1346.67353824 + 80364.97780599032

455982.5429800203

with open(DATA_DIR/'dev-0'/'out.tsv','w') as f_out_file:
    for line in Y_dev_predicted:
        f_out_file.write(str(line))
        f_out_file.write('\n')

Uwaga - regresja linowa działa dobrze tylko dla danych, gdzie występuje korelacja liniowa

Zadanie domowe

• https://gonito.net/challenge/retroc2
• termin 17.05
• należy użyć wektoryzacji (np tf-dif)
• wynik zaliczający to max 50 RMSE dla dev-0
• punkty: 60, dla 3 najlepszych wyników na test-A: 80,