10 KiB
Uczenie maszynowe – zastosowania
14. Autoencoder. Tłumaczenie neuronowe
14.1. Autoencoder
- Uczenie nienadzorowane
- Dane: zbiór nieanotowanych przykładów uczących $\{ x^{(1)}, x^{(2)}, x^{(3)}, \ldots \}$, $x^{(i)} \in \mathbb{R}^{n}$
Autoencoder (encoder-decoder)
Sieć neuronowa taka, że:
- warstwa wejściowa ma $n$ neuronów
- warstwa wyjściowa ma $n$ neuronów
- warstwa środkowa ma $k < n$ neuronów
- $y^{(i)} = x^{(i)}$ dla każdego $i$
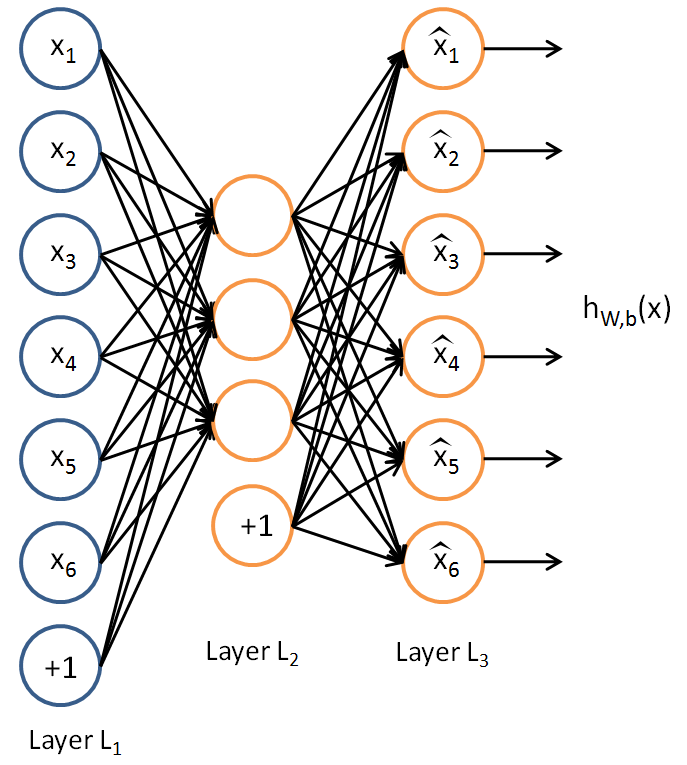
Co otrzymujemy dzięki takiej sieci?
- $y^{(i)} = x^{(i)} ; \Longrightarrow ;$ Autoencoder próbuje nauczyć się funkcji $h(x) \approx x$, czyli funkcji identycznościowej.
- Warstwy środkowe mają mniej neuronów niż warstwy zewnętrzne, więc żeby to osiągnąć, sieć musi znaleźć bardziej kompaktową (tu: $k$-wymiarową) reprezentację informacji zawartej w wektorach $x_{(i)}$.
- Otrzymujemy metodę kompresji danych.
Innymi słowy:
- Ograniczenia nałożone na reprezentację danych w warstwie ukrytej pozwala na „odkrycie” pewnej struktury w danych.
- _Decoder musi odtworzyć do pierwotnej postaci reprezentację danych skompresowaną przez encoder.
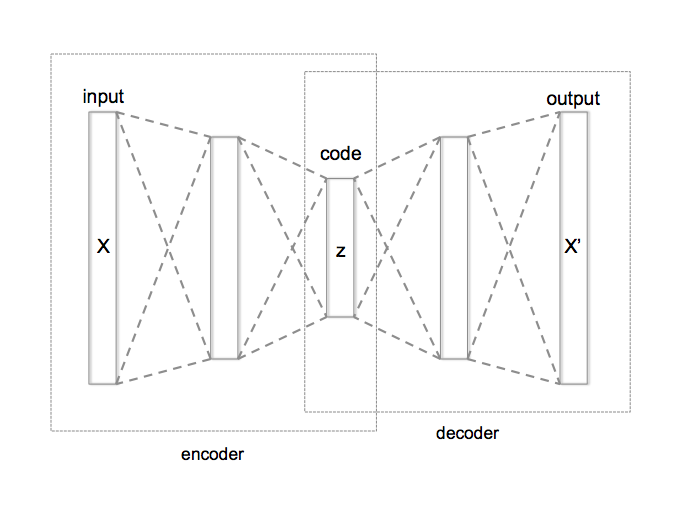
- Całkowita liczba warstw w sieci autoencodera może być większa niż 3.
- Jako funkcji kosztu na ogół używa się błędu średniokwadratowego (_mean squared error, MSE) lub entropii krzyżowej (binary crossentropy).
- Autoencoder może wykryć ciekawe struktury w danych nawet jeżeli $k \geq n$, jeżeli na sieć nałoży się inne ograniczenia.
- W wyniku działania autoencodera uzyskujemy na ogół kompresję stratną.
Autoencoder a PCA
Widzimy, że autoencoder można wykorzystać do redukcji liczby wymiarów. Podobną rolę pełni poznany na jednym z poprzednich wykładów algorytm PCA (analiza głównych składowych, _principal component analysis). Faktycznie, jeżeli zastosujemy autoencoder z liniowymi funkcjami aktywacji i pojedynczą sigmoidalną warstwą ukrytą, to na podstawie uzyskanych wag można odtworzyć główne składowe używając rozkładu według wartości osobliwych (singular value decomposition, SVD).
Autoencoder odszumiający
Jeżeli na wejściu zamiast „czystych” danych użyjemy danych zaszumionych, to otrzymamy sieć, która może usuwać szum z danych:

Autoencoder – zastosowania
Autoencoder sprawdza się gorzej niż inne algorytmy kompresji, więc nie stosuje się go raczej jako metody kompresji danych, ale ma inne zastosowania:
- odszumianie danych
- redukcja wymiarowości
- VAE (_variational autoencoders) – http://kvfrans.com/variational-autoencoders-explained/
14.2. Word embeddings
_Word embeddings – sposoby reprezentacji słów jako wektorów liczbowych
Znaczenie wyrazu jest reprezentowane przez sąsiednie wyrazy:
“A word is characterized by the company it keeps.” (John R. Firth, 1957)
- Pomysł pojawił sie jeszcze w latach 60. XX w.
- _Word embeddings można uzyskiwać na różne sposoby, ale dopiero w ostatnim dziesięcioleciu stało się opłacalne użycie w tym celu sieci neuronowych.
Przykład – 2 zdania:
- "have a good day"
- "have a great day"
Słownik:
- {"a", "day", "good", "great", "have"}
- Aby wykorzystać metody uczenia maszynowego do analizy danych tekstowych, musimy je jakoś reprezentować jako liczby.
- Najprostsza metoda to wektory jednostkowe:
- "a" = $(1, 0, 0, 0, 0)$
- "day" = $(0, 1, 0, 0, 0)$
- "good" = $(0, 0, 1, 0, 0)$
- "great" = $(0, 0, 0, 1, 0)$
- "have" = $(0, 0, 0, 0, 1)$
- Taka metoda nie uwzględnia jednak podobieństw i różnic między znaczeniami wyrazów.
Metody uzyskiwania _word embeddings:
- Common Bag of Words (CBOW)
- Skip Gram
Obie opierają się na odpowiednim użyciu autoencodera.
Skip Gram a CBOW
- Skip Gram lepiej reprezentuje rzadkie wyrazy i lepiej działa, jeżeli mamy mało danych.
- CBOW jest szybszy i lepiej reprezentuje częste wyrazy.
Popularne modele _word embeddings
- Word2Vec (Google)
- GloVe (Stanford)
- FastText (Facebook)
14.3. Tłumaczenie neuronowe
_Neural Machine Translation (NMT)
Neuronowe tłumaczenie maszynowe również opiera się na modelu _encoder-decoder:
- _Encoder koduje z języka źródłowego na abstrakcyjną reprezentację.
- _Decoder odkodowuje z abstrakcyjnej reprezentacji na język docelowy.





