umz21/wyk/11_Wielowarstwowe_sieci_neuronowe.ipynb

Uczenie maszynowe – zastosowania

11. Wielowarstwowe sieci neuronowe w praktyce

11.1. Funkcje aktywacji

• Złożenie funkcji liniowych jest funkcją liniową.
• Głównym zadaniem funkcji aktywacji jest wprowadzenie nieliniowości do sieci neuronowej, żeby model mógł odwzorowywać nie tylko liniowe zależności między danymi.
• Każda funkcja aktywacji ma swoje zalety i wady.
• Różne rodzaje funkcji aktywacji nadają się do różnych zastosowań.

%matplotlib inline

import math
import matplotlib.pyplot as plt
import numpy as np
import random

from IPython.display import YouTubeVideo

def plot(fun):
    x = np.arange(-3.0, 3.0, 0.01)
    y = [fun(x_i) for x_i in x]
    fig = plt.figure(figsize=(14, 7))
    ax = fig.add_subplot(111)
    fig.subplots_adjust(left=0.1, right=0.9, bottom=0.1, top=0.9)
    ax.set_xlim(-3.0, 3.0)
    ax.set_ylim(-1.5, 1.5)
    ax.grid()
    ax.plot(x, y)
    plt.show()

Funkcja logistyczna

$$ g(x) = \frac{1}{1 + e^{-x}} $$

• Przyjmuje wartości z przedziału $(0, 1)$.

# Wykres funkcji logistycznej
plot(lambda x: 1 / (1 + math.exp(-x)))

Tangens hiperboliczny

$$ g(x) = \tanh x = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} $$

• Przyjmuje wartości z przedziału $(-1, 1)$.
• Powstaje z funkcji logistycznej przez przeskalowanie i przesunięcie.

# Wykres funkcji tangensa hiperbolicznego
plot(lambda x: math.tanh(x))

ReLU (_Rectifier Linear Unit)

$$ g(x) = \max(0, x) $$

ReLU – zalety

• Mniej podatna na problem zanikającego gradientu (_vanishing gradient) niż funkcje sigmoidalne, dzięki czemu SGD jest szybciej zbieżna.
• Prostsze obliczanie gradientu.
• Dzięki zerowaniu ujemnych wartości, wygasza neurony, „rozrzedzając” sieć (_sparsity), co przyspiesza obliczenia.

ReLU – wady

• Dla dużych wartości gradient może „eksplodować”.
• „Wygaszanie” neuronów.

# Wykres fukncji ReLU
plot(lambda x: max(0, x))

Softplus

$$ g(x) = \log(1 + e^{x}) $$

• Wygładzona wersja ReLU.

# Wykres funkcji softplus
plot(lambda x: math.log(1 + math.exp(x)))

Problem zanikającego gradientu (_vanishing gradient problem)

• Sigmoidalne funkcje aktywacji ograniczają wartości na wyjściach neuronów do niewielkich przedziałów ($(-1, 1)$, $(0, 1)$ itp.).
• Jeżeli sieć ma wiele warstw, to podczas propagacji wstecznej mnożymy przez siebie wiele małych wartości → obliczony gradient jest mały.
• Im więcej warstw, tym silniejszy efekt zanikania.

Sposoby na zanikający gradient

• Modyfikacja algorytmu optymalizacji (_RProp, RMSProp)
• Użycie innej funckji aktywacji (ReLU, softplus)
• Dodanie warstw _dropout
• Nowe architektury (LSTM itp.)
• Więcej danych, zwiększenie mocy obliczeniowej

11.2. Odmiany metody gradientu prostego

• Batch gradient descent
• Stochastic gradient descent
• Mini-batch gradient descent

_Batch gradient descent

• Klasyczna wersja metody gradientu prostego
• Obliczamy gradient funkcji kosztu względem całego zbioru treningowego: $$ \theta := \theta - \alpha \cdot \nabla_\theta J(\theta) $$
• Dlatego może działać bardzo powoli
• Nie można dodawać nowych przykładów na bieżąco w trakcie trenowania modelu (_online learning)

_Stochastic gradient descent (SGD)

• Aktualizacja parametrów dla każdego przykładu: $$ \theta := \theta - \alpha \cdot \nabla_\theta , J ! \left( \theta, x^{(i)}, y^{(i)} \right) $$
• Dużo szybszy niż _batch gradient descent
• Można dodawać nowe przykłady na bieżąco w trakcie trenowania (_online learning)

• Częsta aktualizacja parametrów z dużą wariancją:

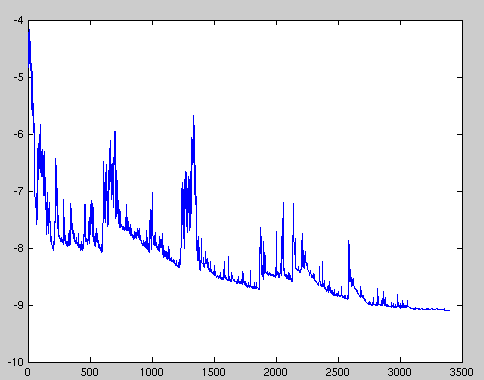
• Z jednej strony dzięki temu uczenie nie "utyka" w złych minimach lokalnych, ale z drugiej strony może „wyskoczyć” z dobrego minimum

_Mini-batch gradient descent

• Kompromis między _batch gradient descent i SGD $$ \theta := \theta - \alpha \cdot \nabla_\theta , J \left( \theta, x^{(i : i+n)}, y^{(i : i_n)} \right) $$
• Stabilniejsza zbieżność dzięki redukcji wariancji aktualizacji parametrów
• Szybszy niż klasyczny _batch gradient descent
• Typowa wielkość batcha: między 50 a 256 przykładów

Wady klasycznej metody gradientu prostego, czyli dlaczego potrzebujemy optymalizacji

• Trudno dobrać właściwą szybkość uczenia (_learning rate)
• Jedna ustalona wartość stałej uczenia się dla wszystkich parametrów
• Funkcja kosztu dla sieci neuronowych nie jest wypukła, więc uczenie może utknąć w złym minimum lokalnym lub punkcie siodłowym

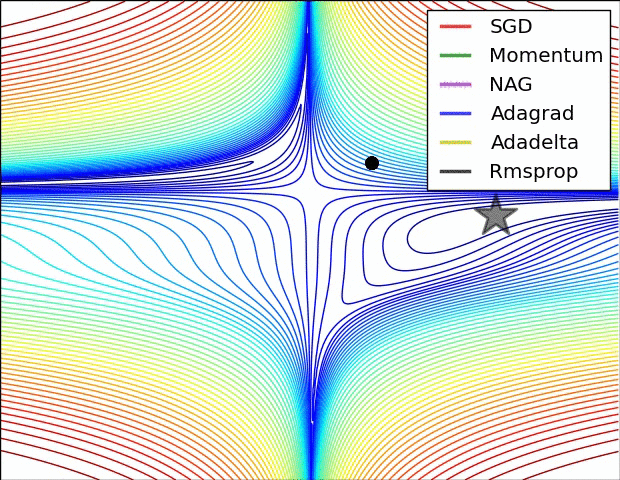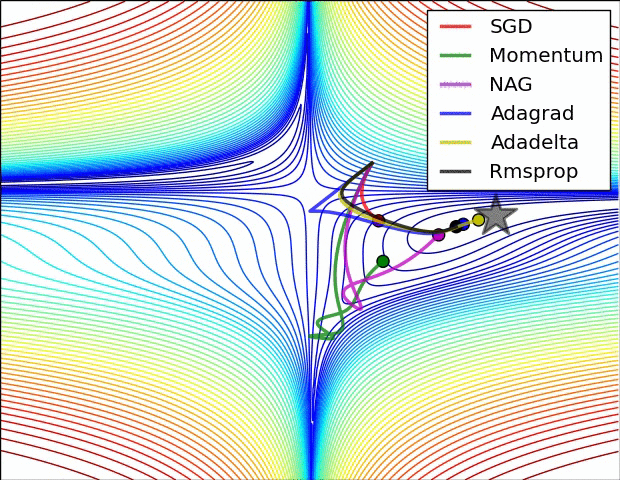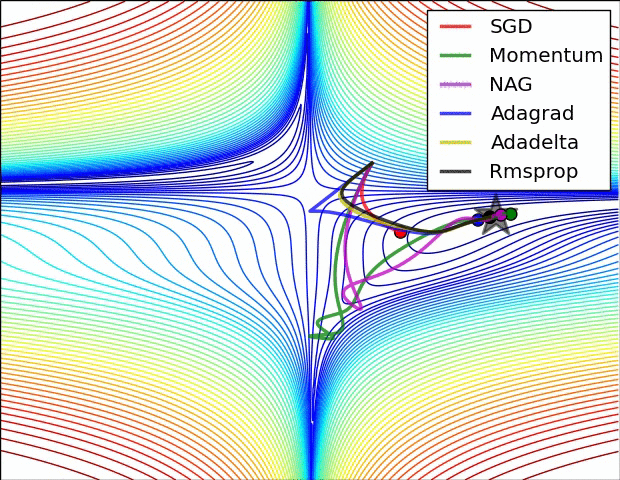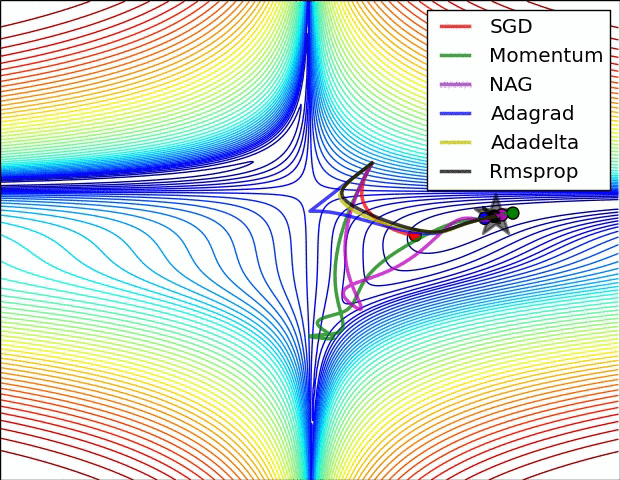
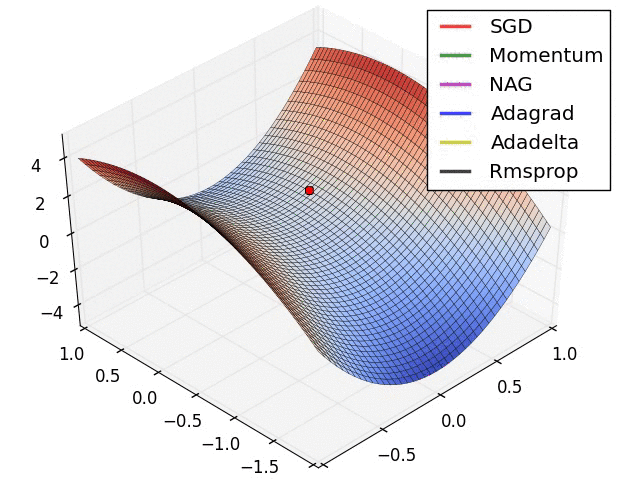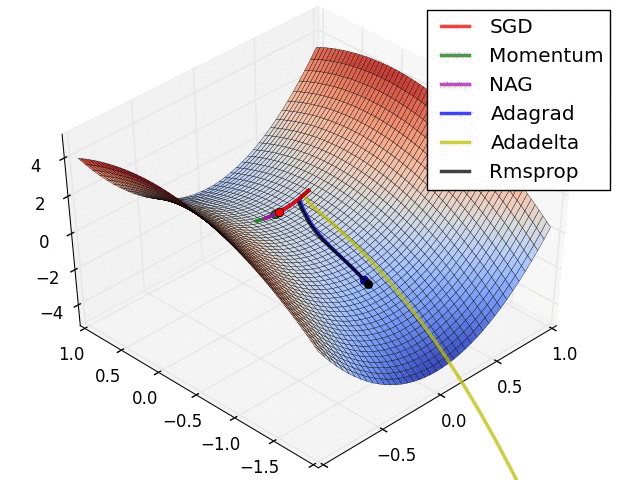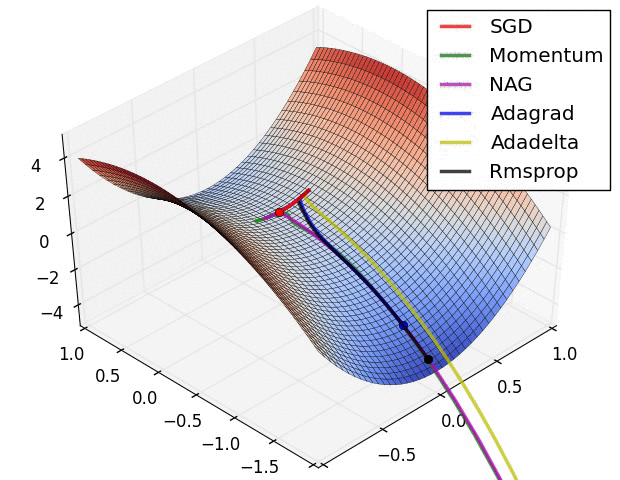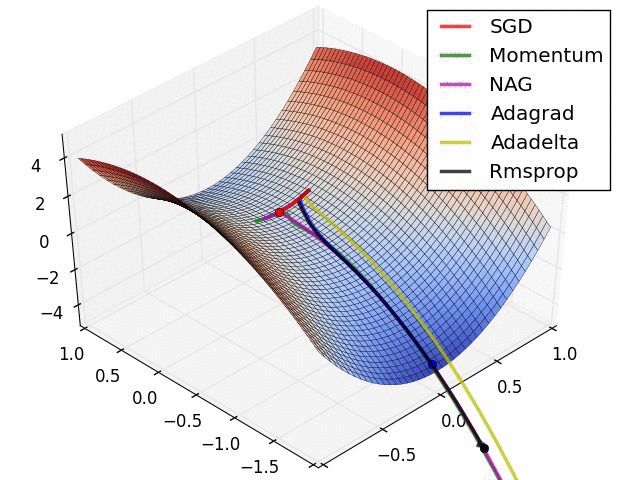
11.3. Algorytmy optymalizacji metody gradientu

• Momentum
• Nesterov Accelerated Gradient
• Adagrad
• Adadelta
• RMSprop
• Adam
• Nadam
• AMSGrad

Momentum

• SGD źle radzi sobie w „wąwozach” funkcji kosztu
• Momentum rozwiązuje ten problem przez dodanie współczynnika $\gamma$, który można trakować jako „pęd” spadającej piłki: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta) $$ $$ \theta := \theta - v_t $$

Przyspiesony gradient Nesterova (_Nesterov Accelerated Gradient, NAG)

• Momentum czasami powoduje niekontrolowane rozpędzanie się piłki, przez co staje się „mniej sterowna”
• Nesterov do piłki posiadającej pęd dodaje „hamulec”, który spowalnia piłkę przed wzniesieniem: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta - \gamma , v_{t-1}) $$ $$ \theta := \theta - v_t $$

Adagrad

• “Adaptive gradient”
• Adagrad dostosowuje współczynnik uczenia (_learning rate) do parametrów: zmniejsza go dla cech występujących częściej, a zwiększa dla występujących rzadziej
• Świetny do trenowania na rzadkich (_sparse) zbiorach danych
• Wada: współczynnik uczenia może czasami gwałtownie maleć

Adadelta i RMSprop

• Warianty algorytmu Adagrad, które radzą sobie z problemem gwałtownych zmian współczynnika uczenia

Adam

• “Adaptive moment estimation”
• Łączy zalety algorytmów RMSprop i Momentum
• Można go porównać do piłki mającej ciężar i opór
• Obecnie jeden z najpopularniejszych algorytmów optymalizacji

Nadam

• “Nesterov-accelerated adaptive moment estimation”
• Łączy zalety algorytmów Adam i Nesterov Accelerated Gradient

AMSGrad

• Wariant algorytmu Adam lepiej dostosowany do zadań takich jak rozpoznawanie obiektów czy tłumaczenie maszynowe