pms/umz21

Fork 1

Paweł Skórzewski a6e1f3315d Materiały na podstawie ubiegłorocznych

2021-03-02 08:32:40 +01:00

145 KiB

Raw Blame History

Uczenie maszynowe UMZ 2019/2020

26 maja 2020

11. Wielowarstwowe sieci neuronowe i algorytmy optymalizacji

11.1. Funkcje aktywacji

Każda funkcja aktywacji ma swoje zalety i wady.
Różne rodzaje funkcji aktywacji nadają się do różnych zastosowań.

%matplotlib inline

import math
import matplotlib.pyplot as plt
import numpy as np
import random

import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, SimpleRNN, LSTM
from keras.optimizers import Adagrad, Adam, RMSprop, SGD

from IPython.display import YouTubeVideo

/home/pawel/.local/lib/python2.7/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
  from ._conv import register_converters as _register_converters
Using TensorFlow backend.

def plot(fun):
    x = np.arange(-3.0, 3.0, 0.01)
    y = [fun(x_i) for x_i in x]
    fig = plt.figure(figsize=(14, 7))
    ax = fig.add_subplot(111)
    fig.subplots_adjust(left=0.1, right=0.9, bottom=0.1, top=0.9)
    ax.set_xlim(-3.0, 3.0)
    ax.set_ylim(-1.5, 1.5)
    ax.grid()
    ax.plot(x, y)
    plt.show()

Funkcja logistyczna

$$ g(x) = \frac{1}{1 + e^{-x}} $$

Przyjmuje wartości z przedziału $(0, 1)$.

Funkcja logistyczna – wykres

plot(lambda x: 1 / (1 + math.exp(-x)))

Tangens hiperboliczny

$$ g(x) = \tanh x = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} $$

Przyjmuje wartości z przedziału $(-1, 1)$.
Powstaje z funkcji logistycznej przez przeskalowanie i przesunięcie.

Tangens hiperboliczny – wykres

plot(lambda x: math.tanh(x))

ReLU (_Rectifier Linear Unit)

$$ g(x) = \max(0, x) $$

ReLU – zalety

Mniej podatna na problem zanikającego gradientu (_vanishing gradient) niż funkcje sigmoidalne, dzięki czemu SGD jest szybciej zbieżna.
Prostsze obliczanie gradientu.
Dzięki zerowaniu ujemnych wartości, wygasza neurony, „rozrzedzając” sieć (_sparsity), co przyspiesza obliczenia.

ReLU – wady

Dla dużych wartości gradient może „eksplodować”.
„Wygaszanie” neuronów.

ReLU – wykres

plot(lambda x: max(0, x))

Softplus

$$ g(x) = \log(1 + e^{x}) $$

Wygładzona wersja ReLU.

Softplus – wykres

plot(lambda x: math.log(1 + math.exp(x)))

Problem zanikającego gradientu (_vanishing gradient problem)

Sigmoidalne funkcje aktywacji ograniczają wartości na wyjściach neuronów do niewielkich przedziałów ($(-1, 1)$, $(0, 1)$ itp.).
Jeżeli sieć ma wiele warstw, to podczas propagacji wstecznej mnożymy przez siebie wiele małych wartości → obliczony gradient jest mały.
Im więcej warstw, tym silniejszy efekt zanikania.

Sposoby na zanikający gradient

Modyfikacja algorytmu optymalizacji (_RProp, RMSProp)
Użycie innej funckji aktywacji (ReLU, softplus)
Dodanie warstw _dropout
Nowe architektury (LSTM itp.)
Więcej danych, zwiększenie mocy obliczeniowej

11.2. Wielowarstwowe sieci neuronowe w praktyce

Przykład: MNIST

_Modified National Institute of Standards and Technology database

Zbiór cyfr zapisanych pismem odręcznym
60 000 przykładów uczących, 10 000 przykładów testowych
Rozdzielczość każdego przykładu: 28 × 28 = 784 piksele

# źródło: https://github.com/keras-team/keras/examples/minst_mlp.py

import keras
from keras.datasets import mnist

# załaduj dane i podziel je na zbiory uczący i testowy
(x_train, y_train), (x_test, y_test) = mnist.load_data()

def draw_examples(examples, captions=None):
    plt.figure(figsize=(16, 4))
    m = len(examples)
    for i, example in enumerate(examples):
        plt.subplot(100 + m * 10 + i + 1)
        plt.imshow(example, cmap=plt.get_cmap('gray'))
    plt.show()
    if captions is not None:
        print(6 * ' ' + (10 * ' ').join(str(captions[i]) for i in range(m)))

draw_examples(x_train[:7], captions=y_train)

      5          0          4          1          9          2          1

num_classes = 10

x_train = x_train.reshape(60000, 784)  # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('{} przykładów uczących'.format(x_train.shape[0]))
print('{} przykładów testowych'.format(x_test.shape[0]))

# przekonwertuj wektory klas na binarne macierze klas
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

60000 przykładów uczących
10000 przykładów testowych

model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 512)               401920    
_________________________________________________________________
dropout_1 (Dropout)          (None, 512)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 512)               262656    
_________________________________________________________________
dropout_2 (Dropout)          (None, 512)               0         
_________________________________________________________________
dense_3 (Dense)              (None, 10)                5130      
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________

print(x_train.shape, y_train.shape)

((60000, 784), (60000, 10))

model.compile(loss='categorical_crossentropy', optimizer=RMSprop(), metrics=['accuracy'])

model.fit(x_train, y_train, batch_size=128, epochs=5, verbose=1,
          validation_data=(x_test, y_test))

Train on 60000 samples, validate on 10000 samples
Epoch 1/5
60000/60000 [==============================] - 9s 153us/step - loss: 0.2489 - acc: 0.9224 - val_loss: 0.1005 - val_acc: 0.9706
Epoch 2/5
60000/60000 [==============================] - 9s 151us/step - loss: 0.1042 - acc: 0.9683 - val_loss: 0.0861 - val_acc: 0.9740
Epoch 3/5
60000/60000 [==============================] - 9s 153us/step - loss: 0.0742 - acc: 0.9782 - val_loss: 0.0733 - val_acc: 0.9796
Epoch 4/5
60000/60000 [==============================] - 9s 154us/step - loss: 0.0603 - acc: 0.9824 - val_loss: 0.0713 - val_acc: 0.9800
Epoch 5/5
60000/60000 [==============================] - 9s 157us/step - loss: 0.0512 - acc: 0.9848 - val_loss: 0.0749 - val_acc: 0.9795

<keras.callbacks.History at 0x7fdda4f97110>

score = model.evaluate(x_test, y_test, verbose=0)

print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))

Test loss: 0.074858742202
Test accuracy: 0.9795

Warstwa _dropout to metoda regularyzacji, służy zapobieganiu nadmiernemu dopasowaniu sieci. Polega na tym, że część węzłów sieci jest usuwana w sposób losowy.

# Bez warstw Dropout

num_classes = 10

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.reshape(60000, 784)  # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255

y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

model_no_dropout = Sequential()
model_no_dropout.add(Dense(512, activation='relu', input_shape=(784,)))
model_no_dropout.add(Dense(512, activation='relu'))
model_no_dropout.add(Dense(num_classes, activation='softmax'))
model_no_dropout.summary()

model_no_dropout.compile(loss='categorical_crossentropy',
                         optimizer=RMSprop(),
                         metrics=['accuracy'])

model_no_dropout.fit(x_train, y_train,
                     batch_size=128,
                     epochs=5,
                     verbose=1,
                     validation_data=(x_test, y_test))

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_4 (Dense)              (None, 512)               401920    
_________________________________________________________________
dense_5 (Dense)              (None, 512)               262656    
_________________________________________________________________
dense_6 (Dense)              (None, 10)                5130      
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
Train on 60000 samples, validate on 10000 samples
Epoch 1/5
60000/60000 [==============================] - 8s 139us/step - loss: 0.2237 - acc: 0.9303 - val_loss: 0.0998 - val_acc: 0.9676
Epoch 2/5
60000/60000 [==============================] - 8s 136us/step - loss: 0.0818 - acc: 0.9748 - val_loss: 0.0788 - val_acc: 0.9770
Epoch 3/5
60000/60000 [==============================] - 8s 136us/step - loss: 0.0538 - acc: 0.9831 - val_loss: 0.1074 - val_acc: 0.9695
Epoch 4/5
60000/60000 [==============================] - 10s 161us/step - loss: 0.0397 - acc: 0.9879 - val_loss: 0.0871 - val_acc: 0.9763
Epoch 5/5
60000/60000 [==============================] - 12s 195us/step - loss: 0.0299 - acc: 0.9910 - val_loss: 0.0753 - val_acc: 0.9812

<keras.callbacks.History at 0x7fdda3dcad50>

# Bez warstw Dropout

score = model_no_dropout.evaluate(x_test, y_test, verbose=0)

print('Test loss (no dropout): {}'.format(score[0]))
print('Test accuracy (no dropout): {}'.format(score[1]))

Test loss (no dropout): 0.0753162465898
Test accuracy (no dropout): 0.9812

# Więcej warstw, inna funkcja aktywacji

num_classes = 10

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.reshape(60000, 784)  # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255

y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

model3 = Sequential()
model3.add(Dense(2500, activation='tanh', input_shape=(784,)))
model3.add(Dense(2000, activation='tanh'))
model3.add(Dense(1500, activation='tanh'))
model3.add(Dense(1000, activation='tanh'))
model3.add(Dense(500, activation='tanh'))
model3.add(Dense(num_classes, activation='softmax'))
model3.summary()

model3.compile(loss='categorical_crossentropy',
               optimizer=RMSprop(),
               metrics=['accuracy'])

model3.fit(x_train, y_train,
           batch_size=128,
           epochs=10,
           verbose=1,
           validation_data=(x_test, y_test))

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_7 (Dense)              (None, 2500)              1962500   
_________________________________________________________________
dense_8 (Dense)              (None, 2000)              5002000   
_________________________________________________________________
dense_9 (Dense)              (None, 1500)              3001500   
_________________________________________________________________
dense_10 (Dense)             (None, 1000)              1501000   
_________________________________________________________________
dense_11 (Dense)             (None, 500)               500500    
_________________________________________________________________
dense_12 (Dense)             (None, 10)                5010      
=================================================================
Total params: 11,972,510
Trainable params: 11,972,510
Non-trainable params: 0
_________________________________________________________________
Train on 60000 samples, validate on 10000 samples
Epoch 1/10
60000/60000 [==============================] - 145s 2ms/step - loss: 1.4242 - acc: 0.5348 - val_loss: 0.4426 - val_acc: 0.8638
Epoch 2/10
60000/60000 [==============================] - 140s 2ms/step - loss: 0.3245 - acc: 0.9074 - val_loss: 0.2231 - val_acc: 0.9360
Epoch 3/10
60000/60000 [==============================] - 137s 2ms/step - loss: 0.1993 - acc: 0.9420 - val_loss: 0.1694 - val_acc: 0.9485
Epoch 4/10
60000/60000 [==============================] - 136s 2ms/step - loss: 0.1471 - acc: 0.9571 - val_loss: 0.1986 - val_acc: 0.9381
Epoch 5/10
60000/60000 [==============================] - 132s 2ms/step - loss: 0.1189 - acc: 0.9650 - val_loss: 0.1208 - val_acc: 0.9658
Epoch 6/10
60000/60000 [==============================] - 131s 2ms/step - loss: 0.0983 - acc: 0.9711 - val_loss: 0.1260 - val_acc: 0.9637
Epoch 7/10
60000/60000 [==============================] - 129s 2ms/step - loss: 0.0818 - acc: 0.9753 - val_loss: 0.0984 - val_acc: 0.9727
Epoch 8/10
60000/60000 [==============================] - 129s 2ms/step - loss: 0.0710 - acc: 0.9784 - val_loss: 0.1406 - val_acc: 0.9597
Epoch 9/10
60000/60000 [==============================] - 129s 2ms/step - loss: 0.0611 - acc: 0.9811 - val_loss: 0.0987 - val_acc: 0.9727
Epoch 10/10
60000/60000 [==============================] - 136s 2ms/step - loss: 0.0533 - acc: 0.9837 - val_loss: 0.1070 - val_acc: 0.9718

<keras.callbacks.History at 0x7fdd95c86610>

# Więcej warstw, inna funkcja aktywacji

score = model3.evaluate(x_test, y_test, verbose=0)

print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))

Test loss: 0.107020105763
Test accuracy: 0.9718

Przykład: 4-pikselowy aparat fotograficzny

YouTubeVideo('ILsA4nyG7I0', width=800, height=600)

def generate_example(description):
    variant = random.choice([1, -1])
    if description == 's':  # solid
        return (np.array([[ 1.0,  1.0], [ 1.0,  1.0]]) if variant == 1 else
                np.array([[-1.0, -1.0], [-1.0, -1.0]]))
    elif description == 'v':  # vertical
        return (np.array([[ 1.0, -1.0], [ 1.0, -1.0]]) if variant == 1 else
                np.array([[-1.0,  1.0], [-1.0,  1.0]]))
    elif description == 'd':  # diagonal
        return (np.array([[ 1.0, -1.0], [-1.0,  1.0]]) if variant == 1 else
                np.array([[-1.0,  1.0], [ 1.0, -1.0]]))
    elif description == 'h':  # horizontal
        return (np.array([[ 1.0,  1.0], [-1.0, -1.0]]) if variant == 1 else
                np.array([[-1.0, -1.0], [ 1.0,  1.0]]))
    else:
        return np.array([[random.uniform(-1, 1), random.uniform(-1, 1)],
                         [random.uniform(-1, 1), random.uniform(-1, 1)]])

num_classes = 4

trainset_size = 4000
testset_size = 1000

y4_train = np.array([random.choice(['s', 'v', 'd', 'h']) for i in range(trainset_size)])
x4_train = np.array([generate_example(desc) for desc in y4_train])

y4_test = np.array([random.choice(['s', 'v', 'd', 'h']) for i in range(testset_size)])
x4_test = np.array([generate_example(desc) for desc in y4_test])

draw_examples(x4_train[:7], captions=y4_train)

      s          s          d          s          h          s          v

x4_train = x4_train.reshape(trainset_size, 4)
x4_test = x4_test.reshape(testset_size, 4)
x4_train = x4_train.astype('float32')
x4_test = x4_test.astype('float32')

y4_train = np.array([{'s': 0, 'v': 1, 'd': 2, 'h': 3}[desc] for desc in y4_train])
y4_test = np.array([{'s': 0, 'v': 1, 'd': 2, 'h': 3}[desc] for desc in y4_test])

y4_train = keras.utils.to_categorical(y4_train, num_classes)
y4_test = keras.utils.to_categorical(y4_test, num_classes)

model4 = Sequential()
model4.add(Dense(4, activation='tanh', input_shape=(4,)))
model4.add(Dense(4, activation='tanh'))
model4.add(Dense(8, activation='relu'))
model4.add(Dense(num_classes, activation='softmax'))
model4.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_16 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_17 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_18 (Dense)             (None, 8)                 40        
_________________________________________________________________
dense_19 (Dense)             (None, 4)                 36        
=================================================================
Total params: 116
Trainable params: 116
Non-trainable params: 0
_________________________________________________________________

model4.layers[0].set_weights(
    [np.array([[ 1.0,  0.0,  1.0,  0.0],
               [ 0.0,  1.0,  0.0,  1.0],
               [ 1.0,  0.0, -1.0,  0.0],
               [ 0.0,  1.0,  0.0, -1.0]],
              dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])
model4.layers[1].set_weights(
    [np.array([[ 1.0, -1.0,  0.0,  0.0],
               [ 1.0,  1.0,  0.0,  0.0],
               [ 0.0,  0.0,  1.0, -1.0],
               [ 0.0,  0.0, -1.0, -1.0]],
              dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])
model4.layers[2].set_weights(
    [np.array([[ 1.0, -1.0,  0.0,  0.0,  0.0,  0.0,  0.0,  0.0],
               [ 0.0,  0.0,  1.0, -1.0,  0.0,  0.0,  0.0,  0.0],
               [ 0.0,  0.0,  0.0,  0.0,  1.0, -1.0,  0.0,  0.0],
               [ 0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  1.0, -1.0]],
              dtype=np.float32), np.array([0., 0., 0., 0., 0., 0., 0., 0.], dtype=np.float32)])

model4.layers[3].set_weights(
    [np.array([[ 1.0,  0.0,  0.0,  0.0],
               [ 1.0,  0.0,  0.0,  0.0],
               [ 0.0,  1.0,  0.0,  0.0],
               [ 0.0,  1.0,  0.0,  0.0],
               [ 0.0,  0.0,  1.0,  0.0],
               [ 0.0,  0.0,  1.0,  0.0],
               [ 0.0,  0.0,  0.0,  1.0],
               [ 0.0,  0.0,  0.0,  1.0]],
              dtype=np.float32), np.array([0., 0., 0., 0.], dtype=np.float32)])

model4.compile(loss='categorical_crossentropy',
               optimizer=Adagrad(),
               metrics=['accuracy'])

for layer in model4.layers:
    print(layer.get_weights())

[array([[ 1.,  0.,  1.,  0.],
       [ 0.,  1.,  0.,  1.],
       [ 1.,  0., -1.,  0.],
       [ 0.,  1.,  0., -1.]], dtype=float32), array([ 0.,  0.,  0.,  0.], dtype=float32)]
[array([[ 1., -1.,  0.,  0.],
       [ 1.,  1.,  0.,  0.],
       [ 0.,  0.,  1., -1.],
       [ 0.,  0., -1., -1.]], dtype=float32), array([ 0.,  0.,  0.,  0.], dtype=float32)]
[array([[ 1., -1.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1., -1.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  1., -1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  1., -1.]], dtype=float32), array([ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.], dtype=float32)]
[array([[ 1.,  0.,  0.,  0.],
       [ 1.,  0.,  0.,  0.],
       [ 0.,  1.,  0.,  0.],
       [ 0.,  1.,  0.,  0.],
       [ 0.,  0.,  1.,  0.],
       [ 0.,  0.,  1.,  0.],
       [ 0.,  0.,  0.,  1.],
       [ 0.,  0.,  0.,  1.]], dtype=float32), array([ 0.,  0.,  0.,  0.], dtype=float32)]

model4.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])

array([[ 0.17831734,  0.17831734,  0.17831734,  0.46504799]], dtype=float32)

score = model4.evaluate(x4_test, y4_test, verbose=0)

print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))

Test loss: 0.765614629269
Test accuracy: 1.0

model5 = Sequential()
model5.add(Dense(4, activation='tanh', input_shape=(4,)))
model5.add(Dense(4, activation='tanh'))
model5.add(Dense(8, activation='relu'))
model5.add(Dense(num_classes, activation='softmax'))
model5.compile(loss='categorical_crossentropy',
               optimizer=RMSprop(),
               metrics=['accuracy'])
model5.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_20 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_21 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_22 (Dense)             (None, 8)                 40        
_________________________________________________________________
dense_23 (Dense)             (None, 4)                 36        
=================================================================
Total params: 116
Trainable params: 116
Non-trainable params: 0
_________________________________________________________________

model5.fit(x4_train, y4_train, epochs=8, validation_data=(x4_test, y4_test))

Train on 4000 samples, validate on 1000 samples
Epoch 1/8
4000/4000 [==============================] - 0s - loss: 1.1352 - acc: 0.5507 - val_loss: 1.0160 - val_acc: 0.7330
Epoch 2/8
4000/4000 [==============================] - 0s - loss: 0.8918 - acc: 0.8722 - val_loss: 0.8094 - val_acc: 0.8580
Epoch 3/8
4000/4000 [==============================] - 0s - loss: 0.6966 - acc: 0.8810 - val_loss: 0.6283 - val_acc: 0.8580
Epoch 4/8
4000/4000 [==============================] - 0s - loss: 0.5284 - acc: 0.8810 - val_loss: 0.4697 - val_acc: 0.8580
Epoch 5/8
4000/4000 [==============================] - 0s - loss: 0.3797 - acc: 0.9022 - val_loss: 0.3312 - val_acc: 1.0000
Epoch 6/8
4000/4000 [==============================] - 0s - loss: 0.2555 - acc: 1.0000 - val_loss: 0.2166 - val_acc: 1.0000
Epoch 7/8
4000/4000 [==============================] - 0s - loss: 0.1612 - acc: 1.0000 - val_loss: 0.1318 - val_acc: 1.0000
Epoch 8/8
4000/4000 [==============================] - 0s - loss: 0.0939 - acc: 1.0000 - val_loss: 0.0732 - val_acc: 1.0000

<keras.callbacks.History at 0x7f4d34067510>

model5.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])

array([[ 0.00708295,  0.00192736,  0.02899081,  0.96199888]], dtype=float32)

score = model5.evaluate(x4_test, y4_test, verbose=0)

print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))

Test loss: 0.0731911802292
Test accuracy: 1.0

import contextlib

@contextlib.contextmanager
def printoptions(*args, **kwargs):
    original = np.get_printoptions()
    np.set_printoptions(*args, **kwargs)
    try:
        yield
    finally: 
        np.set_printoptions(**original)

with printoptions(precision=1, suppress=True):
    for layer in model5.layers:
        print(layer.get_weights())

[array([[-0.2, -0.5,  0.8,  1. ],
       [-0.9,  0.1, -0.8,  0.2],
       [-0.2,  0.4,  0.1, -0.4],
       [-0.8,  0.8,  1. ,  0.3]], dtype=float32), array([ 0. , -0. ,  0.1, -0.1], dtype=float32)]
[array([[-0.4,  0.9, -1.3,  1.7],
       [-0.4, -0.7,  0.3, -0.3],
       [ 0.8, -0.9, -1.1, -0.2],
       [ 1.3,  0.5,  0.4, -0.2]], dtype=float32), array([-0. , -0. ,  0.2,  0. ], dtype=float32)]
[array([[-1.6,  0.3,  0.3, -0.3, -1.1,  1.2,  0.7, -1. ],
       [ 0.4,  1.3, -0.9,  0.8, -0.4, -0.7, -1.2, -1. ],
       [ 0.6,  1. ,  0.9, -1. , -1.1, -0.2, -0.4, -0.3],
       [ 1.1,  0.1, -0.9,  1.3, -0.3, -0.2,  0.2, -0.4]], dtype=float32), array([-0. ,  0.2, -0.1,  0. , -0.1, -0. , -0.1,  0.1], dtype=float32)]
[array([[ 0.6, -1.5,  1.3, -1.4],
       [-0.4, -1.6, -0.3,  1.2],
       [ 1.2,  1.1, -0.3, -1.5],
       [ 0.6,  1.4, -1.5, -1.2],
       [ 0.2, -1.3, -0.9,  0.8],
       [ 0.6, -1.5,  0.8, -1. ],
       [ 0.4, -1.3,  0.4,  0.3],
       [-1.3,  0.5, -0.9,  0.8]], dtype=float32), array([-0.8,  0.7,  0.4,  0.1], dtype=float32)]

12.3. Odmiany metody gradientu prostego

Batch gradient descent
Stochastic gradient descent
Mini-batch gradient descent

_Batch gradient descent

Klasyczna wersja metody gradientu prostego
Obliczamy gradient funkcji kosztu względem całego zbioru treningowego: $$ \theta := \theta - \alpha \cdot \nabla_\theta J(\theta) $$
Dlatego może działać bardzo powoli
Nie można dodawać nowych przykładów na bieżąco w trakcie trenowania modelu (_online learning)

_Stochastic gradient descent (SGD)

Aktualizacja parametrów dla każdego przykładu: $$ \theta := \theta - \alpha \cdot \nabla_\theta , J ! \left( \theta, x^{(i)}, y^{(i)} \right) $$
Dużo szybszy niż _batch gradient descent
Można dodawać nowe przykłady na bieżąco w trakcie trenowania (_online learning)

_Stochastic gradient descent (SGD)

Częsta aktualizacja parametrów z dużą wariancją:

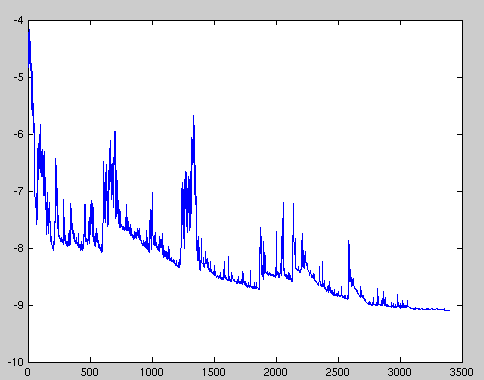
Z jednej strony dzięki temu nie utyka w złych minimach lokalnych, ale z drugiej strony może „wyskoczyć” z dobrego minimum

_Mini-batch gradient descent

Kompromis między _batch gradient descent i SGD $$ \theta := \theta - \alpha \cdot \nabla_\theta , J \left( \theta, x^{(i : i+n)}, y^{(i : i_n)} \right) $$
Stabilniejsza zbieżność dzięki redukcji wariancji aktualizacji parametrów
Szybszy niż klasyczny _batch gradient descent
Typowa wielkość batcha: między 50 a 256 przykładów

Wady klasycznej metody gradientu prostego, czyli dlaczego potrzebujemy optymalizacji

Trudno dobrać właściwą szybkość uczenia (_learning rate)
Jedna ustalona wartość stałej uczenia się dla wszystkich parametrów
Funkcja kosztu dla sieci neuronowych nie jest wypukła, więc uczenie może utknąć w złym minimum lokalnym lub punkcie siodłowym

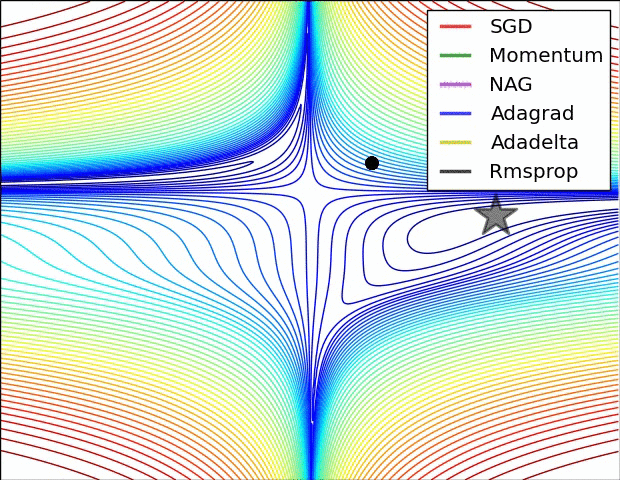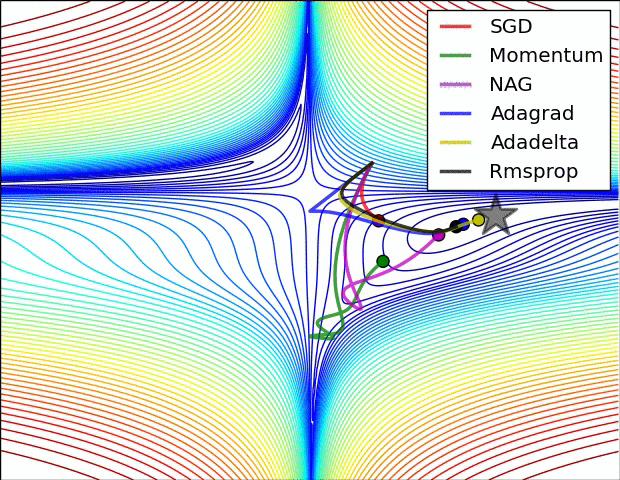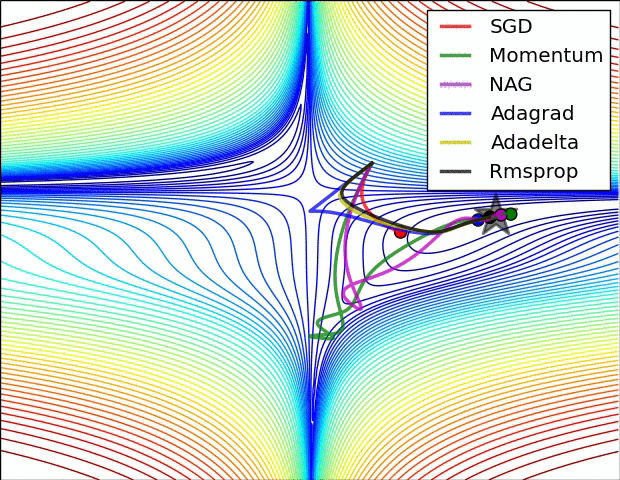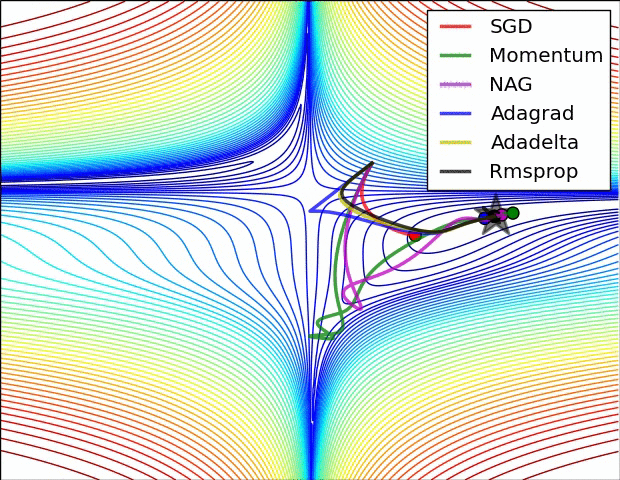
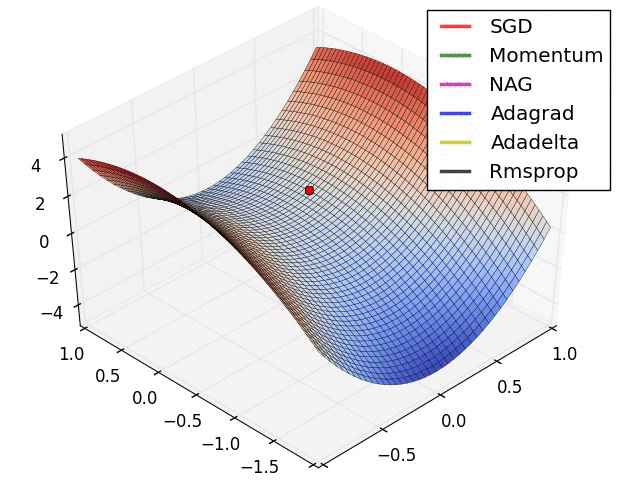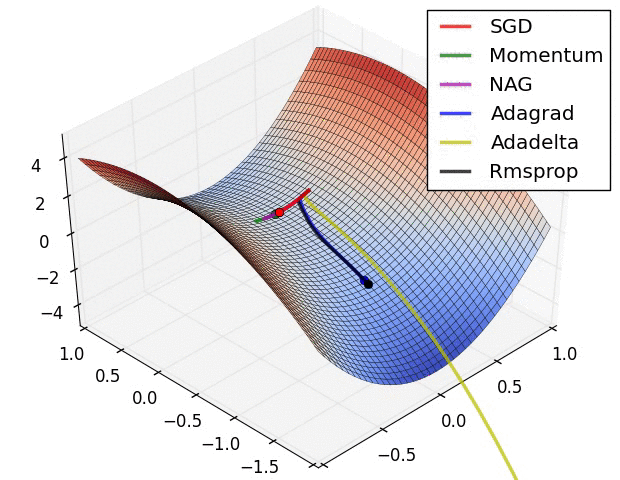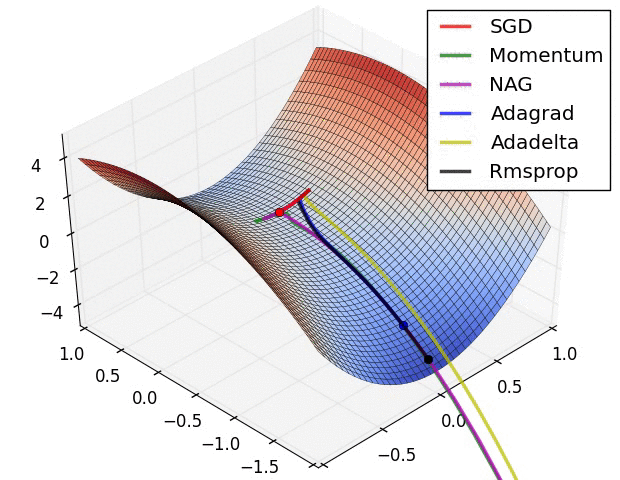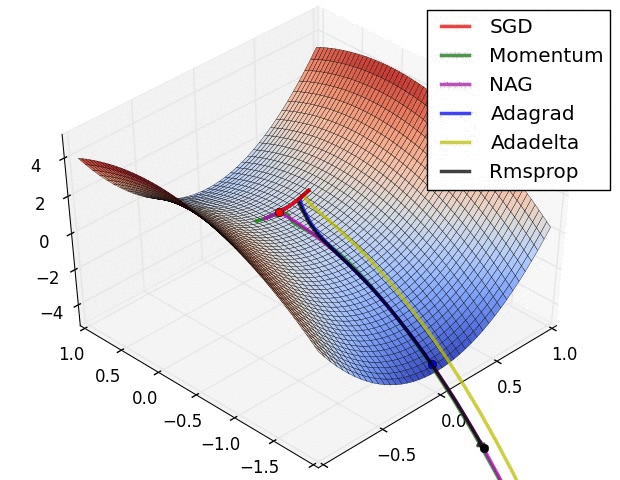
12.4. Algorytmy optymalizacji metody gradientu

Momentum
Nesterov Accelerated Gradient
Adagrad
Adadelta
RMSprop
Adam
Nadam
AMSGrad

Momentum

SGD źle radzi sobie w „wąwozach” funkcji kosztu
Momentum rozwiązuje ten problem przez dodanie współczynnika $\gamma$, który można trakować jako „pęd” spadającej piłki: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta) $$ $$ \theta := \theta - v_t $$

Przyspiesony gradient Nesterova (_Nesterov Accelerated Gradient, NAG)

Momentum czasami powoduje niekontrolowane rozpędzanie się piłki, przez co staje się „mniej sterowna”
Nesterov do piłki posiadającej pęd dodaje „hamulec”, który spowalnia piłkę przed wzniesieniem: $$ v_t := \gamma , v_{t-1} + \alpha , \nabla_\theta J(\theta - \gamma , v_{t-1}) $$ $$ \theta := \theta - v_t $$

Adagrad

“Adaptive gradient”
Adagrad dostosowuje współczynnik uczenia (_learning rate) do parametrów: zmniejsza go dla cech występujących częściej, a zwiększa dla występujących rzadziej
Świetny do trenowania na rzadkich (_sparse) zbiorach danych
Wada: współczynnik uczenia może czasami gwałtownie maleć

Adadelta i RMSprop

Warianty algorytmu Adagrad, które radzą sobie z problemem gwałtownych zmian współczynnika uczenia

Adam

“Adaptive moment estimation”
Łączy zalety algorytmów RMSprop i Momentum
Można go porównać do piłki mającej ciężar i opór
Obecnie jeden z najpopularniejszych algorytmów optymalizacji

Nadam

“Nesterov-accelerated adaptive moment estimation”
Łączy zalety algorytmów Adam i Nesterov Accelerated Gradient

AMSGrad

Wariant algorytmu Adam lepiej dostosowany do zadań takich jak rozpoznawanie obiektów czy tłumaczenie maszynowe

145 KiB Raw Blame History Unescape Escape

Uczenie maszynowe UMZ 2019/2020

26 maja 2020

11. Wielowarstwowe sieci neuronowe i algorytmy optymalizacji

11.1. Funkcje aktywacji

Funkcja logistyczna

Funkcja logistyczna – wykres

Tangens hiperboliczny

Tangens hiperboliczny – wykres

ReLU (_Rectifier Linear Unit)

ReLU – zalety

ReLU – wady

ReLU – wykres

Softplus

Softplus – wykres

Problem zanikającego gradientu (_vanishing gradient problem)

Sposoby na zanikający gradient

11.2. Wielowarstwowe sieci neuronowe w praktyce

Przykład: MNIST

Przykład: 4-pikselowy aparat fotograficzny

12.3. Odmiany metody gradientu prostego

_Batch gradient descent

_Stochastic gradient descent (SGD)

_Stochastic gradient descent (SGD)

_Mini-batch gradient descent

Wady klasycznej metody gradientu prostego, czyli dlaczego potrzebujemy optymalizacji

12.4. Algorytmy optymalizacji metody gradientu

Momentum

Przyspiesony gradient Nesterova (_Nesterov Accelerated Gradient, NAG)

Adagrad

Adadelta i RMSprop

Adam

Nadam

AMSGrad

145 KiB

Raw Blame History