Uczenie maszynowe UMZ 2019/2020

16 czerwca 2020

15. Uczenie przez wzmacnianie i systemy dialogowe

15.1. Uczenie przez wzmacnianie

Paradygmat uczenia przez wzmacnianie

Paradygmat uczenia przez wzmacnianie naśladuje sposób, w jaki uczą się dzieci.
Interakcja ze środowiskiem.

W chwili $t$ agent w stanie $S_t$ podejmuje akcję $A_t$, następnie obserwuje zmianę w środowisku w stanie $S_{t+1}$ i otrzymuje nagrodę $R_{t+1}$:

Celem jest znalezienie takiej taktyki wyboru kolejnej akcji, aby zmaksymalizować wartość końcowej nagrody.

Zastosowanie uczenia przez wzmacnianie:

strategie gier
systemy dialogowe
sterowanie

Uczenie przez wzmacnianie jako proces decyzyjny Markowa

Paradygmat uczenia przez wzmacnianie można formalnie opisać jako proces decyzyjny Markowa: $$ (S, A, T, R) $$ gdzie:

$S$ – skończony zbiór stanów
$A$ – skończony zbiór akcji
$T \colon A \times S \to S$ – funkcja przejścia która opisuje, jak zmienia się środowisko pod wpływem wybranych akcji
$R \colon A \times S \to \mathbb{R}$ – funkcja nagrody

Albo, jeśli przyjmiemy, że środowisko zmienia się w sposób niedeterministyczny: $$ (S, A, P, R) $$ gdzie:

$S$ – skończony zbiór stanów
$A$ – skończony zbiór akcji
$P \colon A \times S \times S \to [0, 1]$ – prawdopodobieństwo przejścia
$R \colon A \times S \times S \to \mathbb{R}$ – funkcja nagrody

Na przykład, prawdopodobieństwo, że akcja $a$ spowoduje przejście ze stanu $s$ do $s'$: $$ P_a(s, s') ; = ; \mathbf{P}( , s_{t+1} = s' , | , s_t = s, a_t = a ,) $$

Strategia

Strategią (_policy) nazywamy odwzorowanie $\pi \colon S \to A$, które bieżącemu stanowi przyporządkuje kolejną akcję do wykonania.
Algorytm uczenia przez wzmacnianie będzie starał się zoptymalizować strategię tak, żeby na koniec otrzymać jak najwyższą nagrodę.
W chwili $t$, ostateczna końcowa nagroda jest zdefiniowana jako: $$ R_t := r_{t+1} + \gamma , r_{t+2} + \gamma^2 , r_{t+3} + \ldots = \sum_{k=0}^T \gamma^k , r_{t+k+1} ; , $$ gdzie $0 < \gamma < 1$ jest czynnikiem, który określa, jak bardzo bieżemy pod uwagę nagrody, które otrzymamy w odległej przyszłości.

Algorytm szuka optymalnej strategii metodą prób i błędów – podejmując akcje i obserwując ich wpływ na środowisko. W podejmowaniu decyzji pomoże mu oszacowanie wartości następujących funkcji:

Funkcja wartości ($V$) odzwierciedla, jak atrakcyjne w dalekiej perspektywie jest przejście do danego stanu: $$ V_{\pi}(s) = \mathbf{E}_{\pi}(R , | , s_t = s) $$
Funkcja $Q$ odzwierciedla, jak atrakcyjne w dalekiej perspektywie jest przejście do danego stanu przez podjęcie danej akcji: $$ Q_{\pi}(s, a) = \mathbf{E}_{\pi}(R , | , s_t = s, a_t = a) $$

Algorytmy uczenia przez wzmacnianie

Programowanie dynamiczne (DP):
- _bootstrapping – aktualizacja oczacowań dla danego stanu na podstawie oszacowań dla możliwych stanów następnych
Metody Monte Carlo (MC)
Uczenie oparte na różnicach czasowych (_temporal difference learning, TD):
- _on-policy – aktualizacja bieżącej strategii:
  - SARSA (_state–action–reward–state–action)
- _off-policy – eksploracja strategii innych niż bieżąca:
  - _Q-Learning
  - _Actor–Critic

Przykład: odwrócone wahadło (_cart and pole)

import IPython
IPython.display.YouTubeVideo('46wjA6dqxOM', width=800, height=600)

Przykład: symulacja autonomicznego samochodu

import IPython
IPython.display.YouTubeVideo('G-GpY7bevuw', width=800, height=600)

15.2. Systemy dialogowe

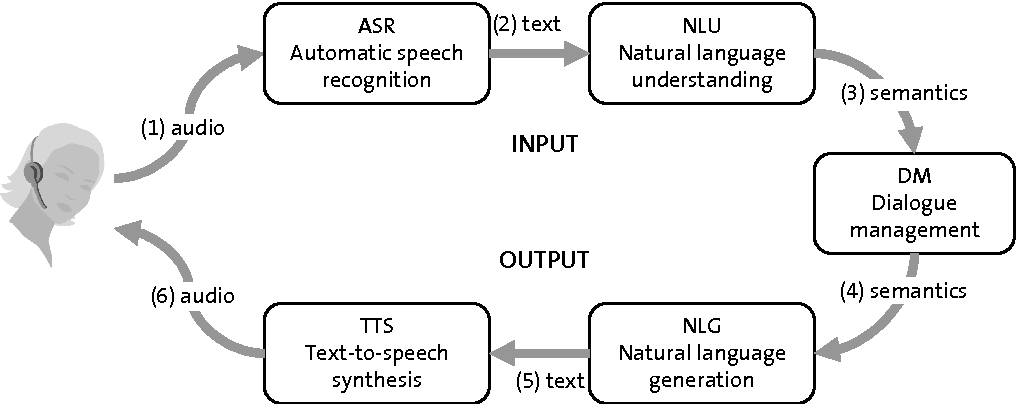
Rodzaje systemów dialogowych

Chatboty
Systemy zorientowane na zadania (_task-oriented systems, goal-oriented systems):
- szukanie informacji
- wypełnianie formularzy
- rozwiązywanie problemów
- systemy edukacyjne i tutorialowe
- inteligentni asystenci

49 KiB Raw Blame History Unescape Escape