pms/umz21

Paweł Skórzewski f869f2e099 Uzupełnienia do wykładów 7 (KNN) i 9 (NN)

2021-05-12 09:26:00 +02:00

69 KiB

Raw Blame History

Uczenie maszynowe – zastosowania

9. Sieci neuronowe – wprowadzenie

# Przydatne importy

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline

9.1. Perceptron

https://www.youtube.com/watch?v=cNxadbrN_aI

Pierwszy perceptron liniowy

Frank Rosenblatt, 1957
aparat fotograficzny podłączony do 400 fotokomórek (rozdzielczość obrazu: 20 x 20)
wagi – potencjometry aktualizowane za pomocą silniczków

Uczenie perceptronu

Cykl uczenia perceptronu Rosenblatta:

Sfotografuj planszę z kolejnym obiektem.
Zaobserwuj, która lampka zapaliła się na wyjściu.
Sprawdź, czy to jest właściwa lampka.
Wyślij sygnał „nagrody” lub „kary”.

Funkcja aktywacji

Funkcja bipolarna:

$$ g(z) = \left\{ \begin{array}{rl} 1 & \textrm{gdy $z > \theta_0$} \\ -1 & \textrm{wpp.} \end{array} \right. $$

gdzie $z = \theta_0x_0 + \ldots + \theta_nx_n$,
$\theta_0$ to próg aktywacji,
$x_0 = 1$.

def bipolar_plot():
    matplotlib.rcParams.update({'font.size': 16})

    plt.figure(figsize=(8,5))
    x = [-1,-.23,1] 
    y = [-1, -1, 1]
    plt.ylim(-1.2,1.2)
    plt.xlim(-1.2,1.2)
    plt.plot([-2,2],[1,1], color='black', ls="dashed")
    plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
    plt.step(x, y, lw=3)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data',0))

    plt.annotate(r'$\theta_0$',
                 xy=(-.23,0), xycoords='data',
                 xytext=(-50, +50), textcoords='offset points', fontsize=26,
                 arrowprops=dict(arrowstyle="->"))

    plt.show()

bipolar_plot()

Perceptron – schemat

Perceptron – zasada działania

Ustal wartości początkowe $\theta$ (wektor 0 lub liczby losowe blisko 0).
Dla każdego przykładu $(x^{(i)}, y^{(i)})$, dla $i=1,\ldots,m$
- Oblicz wartość wyjścia $o^{(i)} = g(\theta^{T}x^{(i)}) = g(\sum_{j=0}^{n} \theta_jx_j^{(i)})$
- Wykonaj aktualizację wag (tzw. _perceptron rule): $$ \theta := \theta + \Delta \theta $$ $$ \Delta \theta = \alpha(y^{(i)}-o^{(i)})x^{(i)} $$

$$\theta_j := \theta_j + \Delta \theta_j $$

Jeżeli przykład został sklasyfikowany poprawnie:

$y^{(i)}=1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(1 - 1)x_j^{(i)} = 0$$
$y^{(i)}=-1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(-1 - -1)x_j^{(i)} = 0$$

Czyli: jeżeli trafiłeś, to nic nie zmieniaj.

$$\theta_j := \theta_j + \Delta \theta_j $$

Jeżeli przykład został sklasyfikowany niepoprawnie:

$y^{(i)}=1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(1 - -1)x_j^{(i)} = 2 \alpha x_j^{(i)}$$
$y^{(i)}=-1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(-1 - 1)x_j^{(i)} = -2 \alpha x_j^{(i)}$$

Czyli: przesuń wagi w odpowiednią stronę.

Perceptron – zalety

intuicyjny i prosty
łatwy w implementacji
jeżeli dane można liniowo oddzielić, algorytm jest zbieżny w skończonym czasie

Perceptron – wady

jeżeli danych nie można oddzielić liniowo, algorytm nie jest zbieżny

def plot_perceptron():
    plt.figure(figsize=(12,3))

    plt.subplot(131)
    plt.ylim(-0.2,1.2)
    plt.xlim(-0.2,1.2)

    plt.title('AND')
    plt.plot([1,0,0], [0,1,0], 'ro', markersize=10)
    plt.plot([1], [1], 'go', markersize=10)

    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('none')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('none')
    ax.spines['left'].set_position(('data',0))

    plt.xticks(np.arange(0, 2, 1.0))
    plt.yticks(np.arange(0, 2, 1.0))


    plt.subplot(132)
    plt.ylim(-0.2,1.2)
    plt.xlim(-0.2,1.2)

    plt.plot([1,0,1], [0,1,1], 'go', markersize=10)
    plt.plot([0], [0], 'ro', markersize=10)

    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('none')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('none')
    ax.spines['left'].set_position(('data',0))

    plt.title('OR')
    plt.xticks(np.arange(0, 2, 1.0))
    plt.yticks(np.arange(0, 2, 1.0))


    plt.subplot(133)
    plt.ylim(-0.2,1.2)
    plt.xlim(-0.2,1.2)

    plt.title('XOR')
    plt.plot([1,0], [0,1], 'go', markersize=10)
    plt.plot([0,1], [0,1], 'ro', markersize=10)

    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('none')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('none')
    ax.spines['left'].set_position(('data',0))

    plt.xticks(np.arange(0, 2, 1.0))
    plt.yticks(np.arange(0, 2, 1.0))

    plt.show()

plot_perceptron()

Funkcje aktywacji

Zamiast funkcji bipolarnej możemy zastosować funkcję sigmoidalną jako funkcję aktywacji.

def plot_activation_functions():
    plt.figure(figsize=(16,7))
    plt.subplot(121)
    x = [-2,-.23,2] 
    y = [-1, -1, 1]
    plt.ylim(-1.2,1.2)
    plt.xlim(-2.2,2.2)
    plt.plot([-2,2],[1,1], color='black', ls="dashed")
    plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
    plt.step(x, y, lw=3)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data',0))

    plt.annotate(r'$\theta_0$',
                 xy=(-.23,0), xycoords='data',
                 xytext=(-50, +50), textcoords='offset points', fontsize=26,
                 arrowprops=dict(arrowstyle="->"))

    plt.subplot(122)
    x2 = np.linspace(-2,2,100)
    y2 = np.tanh(x2+ 0.23)
    plt.ylim(-1.2,1.2)
    plt.xlim(-2.2,2.2)
    plt.plot([-2,2],[1,1], color='black', ls="dashed")
    plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
    plt.plot(x2, y2, lw=3)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data',0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data',0))

    plt.annotate(r'$\theta_0$',
                 xy=(-.23,0), xycoords='data',
                 xytext=(-50, +50), textcoords='offset points', fontsize=26,
                 arrowprops=dict(arrowstyle="->"))

    plt.show()

plot_activation_functions()

Perceptron a regresja liniowa

Uczenie regresji liniowej:

Model: $$h_{\theta}(x) = \sum_{i=0}^n \theta_ix_i$$
Funkcja kosztu (błąd średniokwadratowy): $$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$
Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.

Perceptron a dwuklasowa regresja logistyczna

Uczenie dwuklasowej regresji logistycznej:

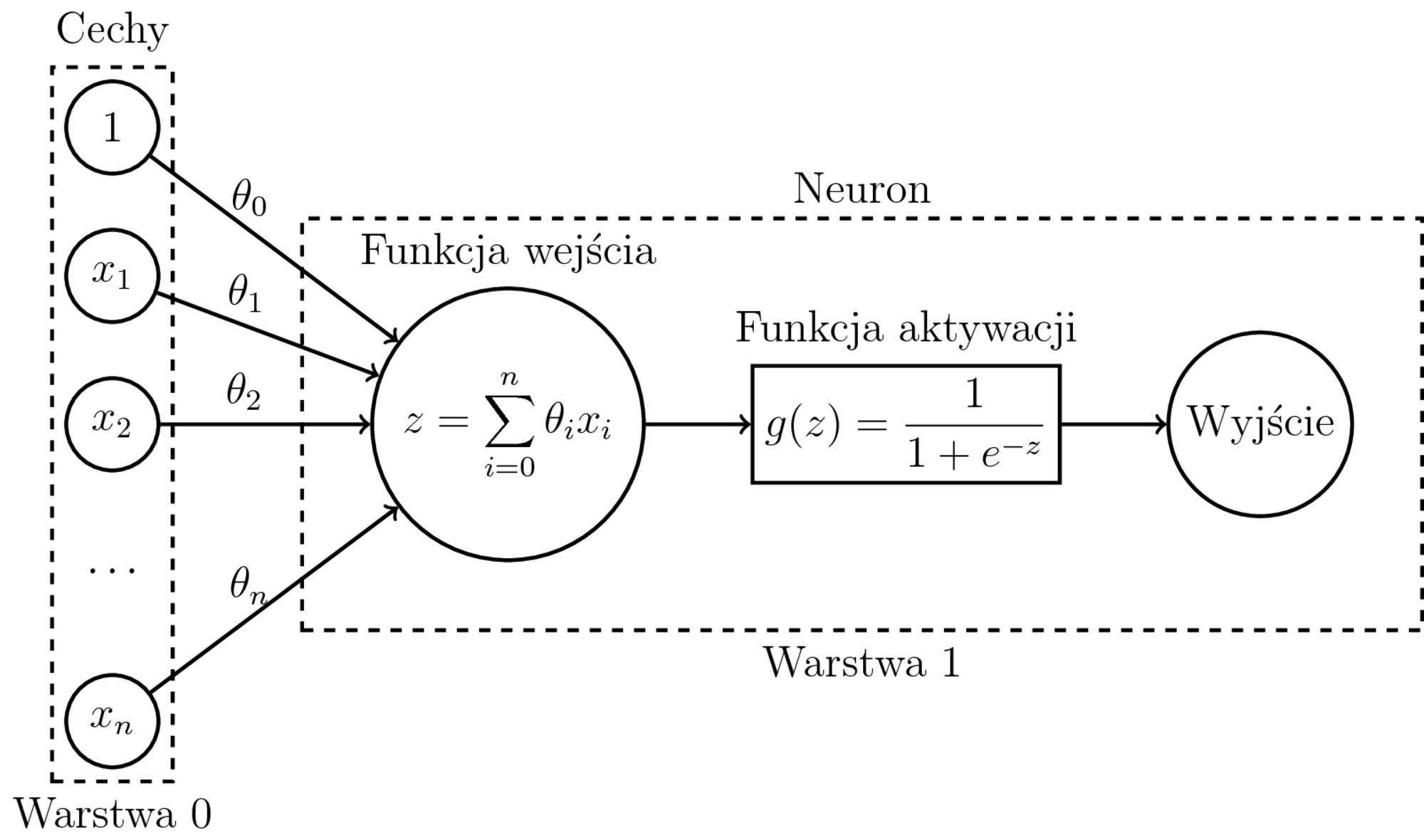
Model: $h_{\theta}(x) = \sigma(\sum_{i=0}^n \theta_ix_i) = P(1|x,\theta)$
Funkcja kosztu (entropia krzyżowa): $$\begin{eqnarray} J(\theta) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(1|x^{(i)},\theta) \\ && + (1-y^{(i)})\log(1-P(1|x^{(i)},\theta)) \big) \end{eqnarray}$$
Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.

Perceptron a wieloklasowa regresja logistyczna

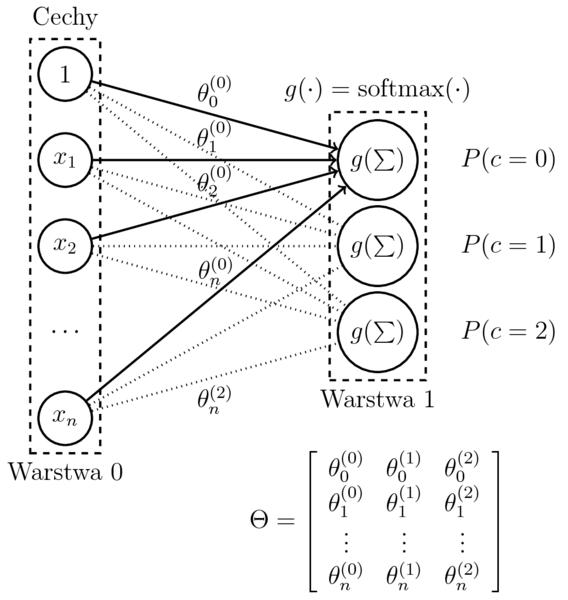
Wieloklasowa regresja logistyczna

Model (dla $c$ klasyfikatorów binarnych): $$\begin{eqnarray} h_{(\theta^{(1)},\dots,\theta^{(c)})}(x) &=& \mathrm{softmax}(\sum_{i=0}^n \theta_{i}^{(1)}x_i, \ldots, \sum_{i=0}^n \theta_i^{(c)}x_i) \\ &=& \left[ P(k|x,\theta^{(1)},\dots,\theta^{(c)}) \right]_{k=1,\dots,c} \end{eqnarray}$$

Funkcja kosztu (przymując model regresji binarnej): $$\begin{eqnarray} J(\theta^{(k)}) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(k|x^{(i)},\theta^{(k)}) \\ && + (1-y^{(i)})\log P(\neg k|x^{(i)},\theta^{(k)}) \big) \end{eqnarray}$$
Po obliczeniu $\nabla J(\theta)$, c-krotne uruchomienie SGD, zastosowanie $\mathrm{softmax}(X)$ do niezależnie uzyskanych klasyfikatorów binarnych.

Przyjmijmy: $$ \Theta = (\theta^{(1)},\dots,\theta^{(c)}) $$

$$h_{\Theta}(x) = \left[ P(k|x,\Theta) \right]_{k=1,\dots,c}$$

$$\delta(x,y) = \left\{\begin{array}{cl} 1 & \textrm{gdy } x=y \\ 0 & \textrm{wpp.}\end{array}\right.$$

Wieloklasowa funkcja kosztu $J(\Theta)$ (kategorialna entropia krzyżowa): $$ J(\Theta) = -\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{c} \delta({y^{(i)},k}) \log P(k|x^{(i)},\Theta) $$

Gradient $\nabla J(\Theta)$: $$ \dfrac{\partial J(\Theta)}{\partial \Theta_{j,k}} = -\frac{1}{m}\sum_{i = 1}^{m} (\delta({y^{(i)},k}) - P(k|x^{(i)}, \Theta)) x^{(i)}_j $$
Liczymy wszystkie wagi jednym uruchomieniem SGD

Podsumowanie

W przypadku jednowarstowej sieci neuronowej wystarczy znać gradient funkcji kosztu.
Wtedy liczymy tak samo jak w przypadku regresji liniowej, logistycznej, wieloklasowej logistycznej itp. (wymienione modele to szczególne przypadki jednowarstwowych sieci neuronowych).
Regresja liniowa i binarna regresja logistyczna to jeden neuron.
Wieloklasowa regresja logistyczna to tyle neuronów, ile klas.

Funkcja aktywacji i funkcja kosztu są dobierane do problemu.

9.2. Wielowarstwowe sieci neuronowe

czyli _Artificial Neural Networks (ANN) lub Multi-Layer Perceptrons (MLP)

Architektura sieci

Sieć neuronowa jako graf neuronów.
Organizacja sieci przez warstwy.
Najczęściej stosowane są sieci jednokierunkowe i gęste.

$n$-warstwowa sieć neuronowa ma $n+1$ warstw (nie liczymy wejścia).
Rozmiary sieci określane poprzez liczbę neuronów lub parametrów.

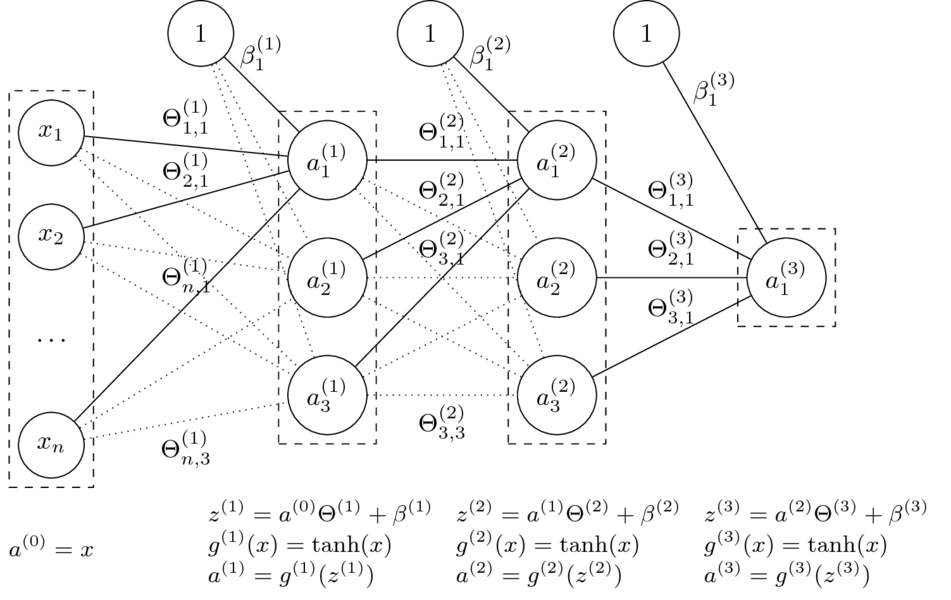
Sieć neuronowa jednokierunkowa (_feedforward)

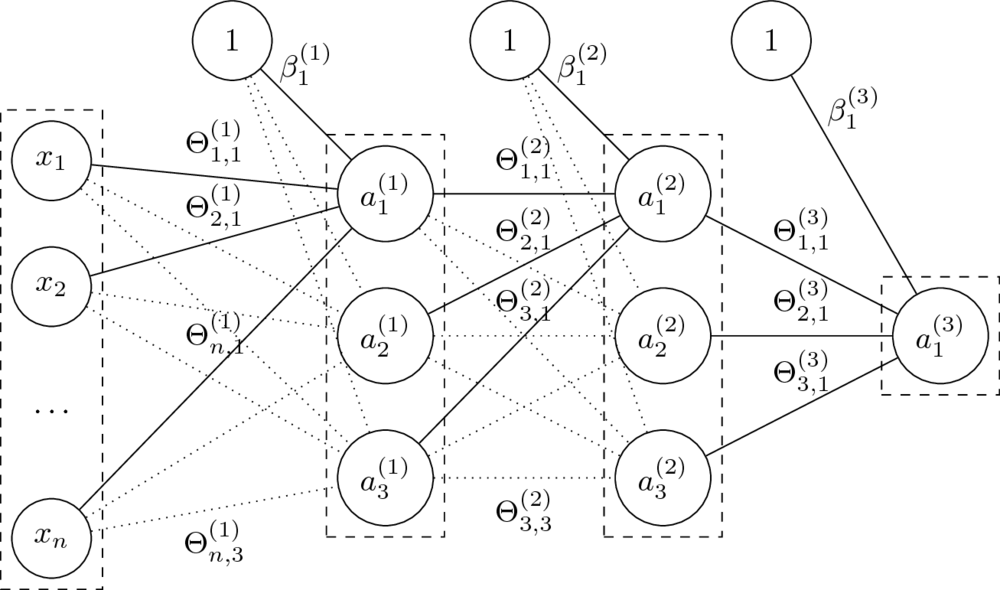
Mając daną $n$-warstwową sieć neuronową oraz jej parametry $\Theta^{(1)}, \ldots, \Theta^{(L)} $ oraz $\beta^{(1)}, \ldots, \beta^{(L)} $ liczymy:

$$a^{(l)} = g^{(l)}\left( a^{(l-1)} \Theta^{(l)} + \beta^{(l)} \right). $$

Funkcje $g^{(l)}$ to tzw. funkcje aktywacji.
Dla $i = 0$ przyjmujemy $a^{(0)} = \mathrm{x}$ (wektor wierszowy cech) oraz $g^{(0)}(x) = x$ (identyczność).

Parametry $\Theta$ to wagi na połączeniach miedzy neuronami dwóch warstw.
Rozmiar macierzy $\Theta^{(l)}$, czyli macierzy wag na połączeniach warstw $a^{(l-1)}$ i $a^{(l)}$, to $\dim(a^{(l-1)}) \times \dim(a^{(l)})$.

Parametry $\beta$ zastępują tutaj dodawanie kolumny z jedynkami do macierzy cech.
Macierz $\beta^{(l)}$ ma rozmiar równy liczbie neuronów w odpowiedniej warstwie, czyli $1 \times \dim(a^{(l)})$.

Klasyfikacja: dla ostatniej warstwy $L$ (o rozmiarze równym liczbie klas) przyjmuje się $g^{(L)}(x) = \mathop{\mathrm{softmax}}(x)$.
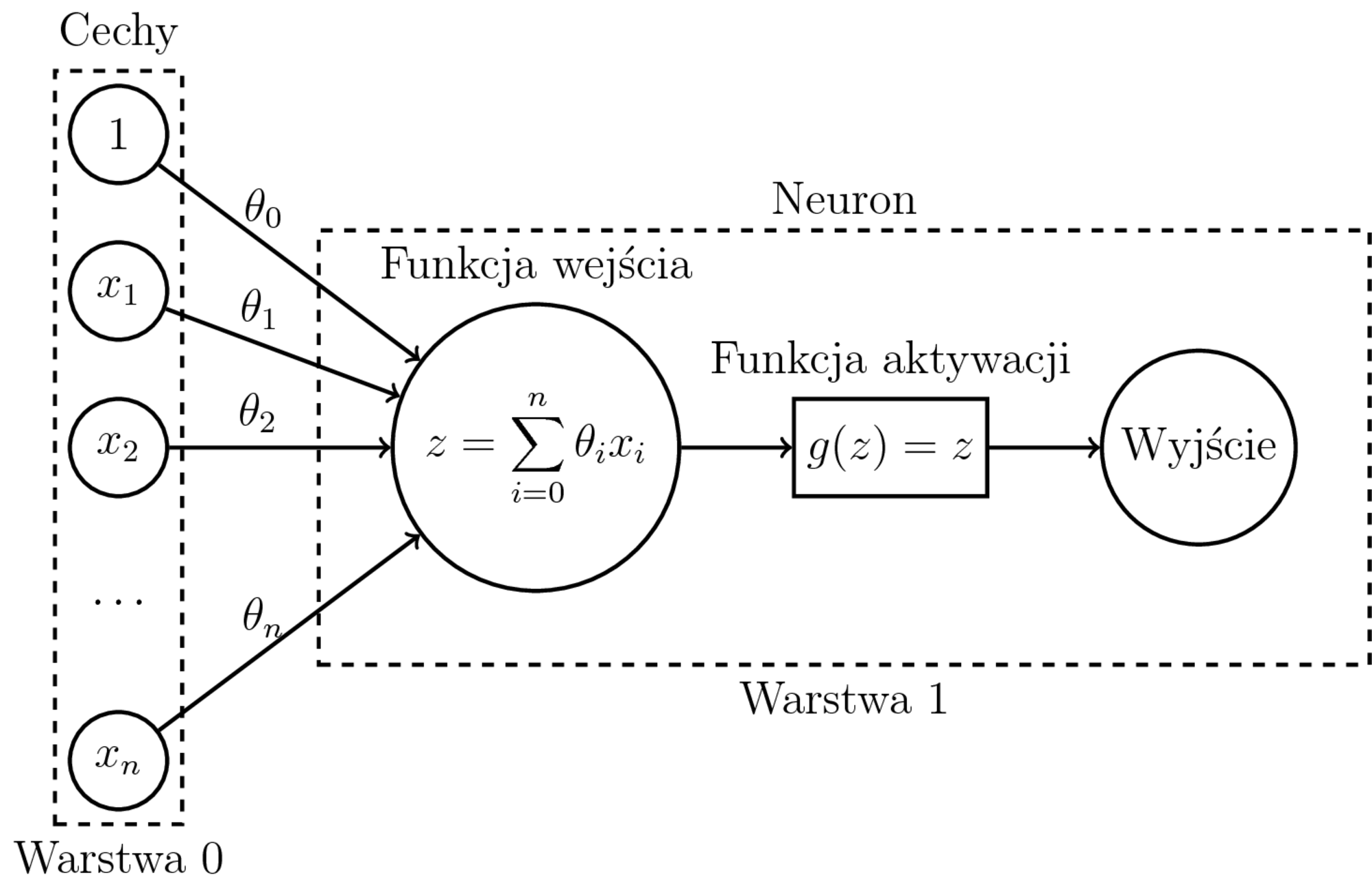
Regresja: pojedynczy neuron wyjściowy jak na obrazku. Funkcją aktywacji może wtedy być np. funkcja identycznościowa.

Pozostałe funkcje aktywacji najcześciej mają postać sigmoidy, np. sigmoidalna, tangens hiperboliczny.
Mogą mieć też inny kształt, np. ReLU, leaky ReLU, maxout.

Uczenie wielowarstwowych sieci neuronowych

Mając algorytm SGD oraz gradienty wszystkich wag, moglibyśmy trenować każdą sieć.

Niech: $$\Theta = (\Theta^{(1)},\Theta^{(2)},\Theta^{(3)},\beta^{(1)},\beta^{(2)},\beta^{(3)})$$
Funkcja sieci neuronowej z grafiki:

$$\small h_\Theta(x) = \tanh(\tanh(\tanh(x\Theta^{(1)}+\beta^{(1)})\Theta^{(2)} + \beta^{(2)})\Theta^{(3)} + \beta^{(3)})$$

Funkcja kosztu dla regresji: $$J(\Theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h_\Theta(x^{(i)})- y^{(i)})^2 $$

Jak obliczymy gradienty?

$$\nabla_{\Theta^{(l)}} J(\Theta) = ? \quad \nabla_{\beta^{(l)}} J(\Theta) = ?$$

Postać funkcji kosztu zależna od wybranej architektury sieci oraz funkcji aktywacji.

$$\small J(\Theta) = \frac{1}{2}(a^{(L)} - y)^2 $$ $$\small \dfrac{\partial}{\partial a^{(L)}} J(\Theta) = a^{(L)} - y$$

$$\small \tanh^{\prime}(x) = 1 - \tanh^2(x)$$

69 KiB Raw Blame History Unescape Escape