s416089/aitech-eks-pub

Fork 0

forked from filipg/aitech-eks-pub

Filip Gralinski ed364e92ca Kontynuacja 3

2021-03-31 15:20:26 +02:00

134 KiB

Raw Blame History

Wyszukiwarka - szybka i sensowna

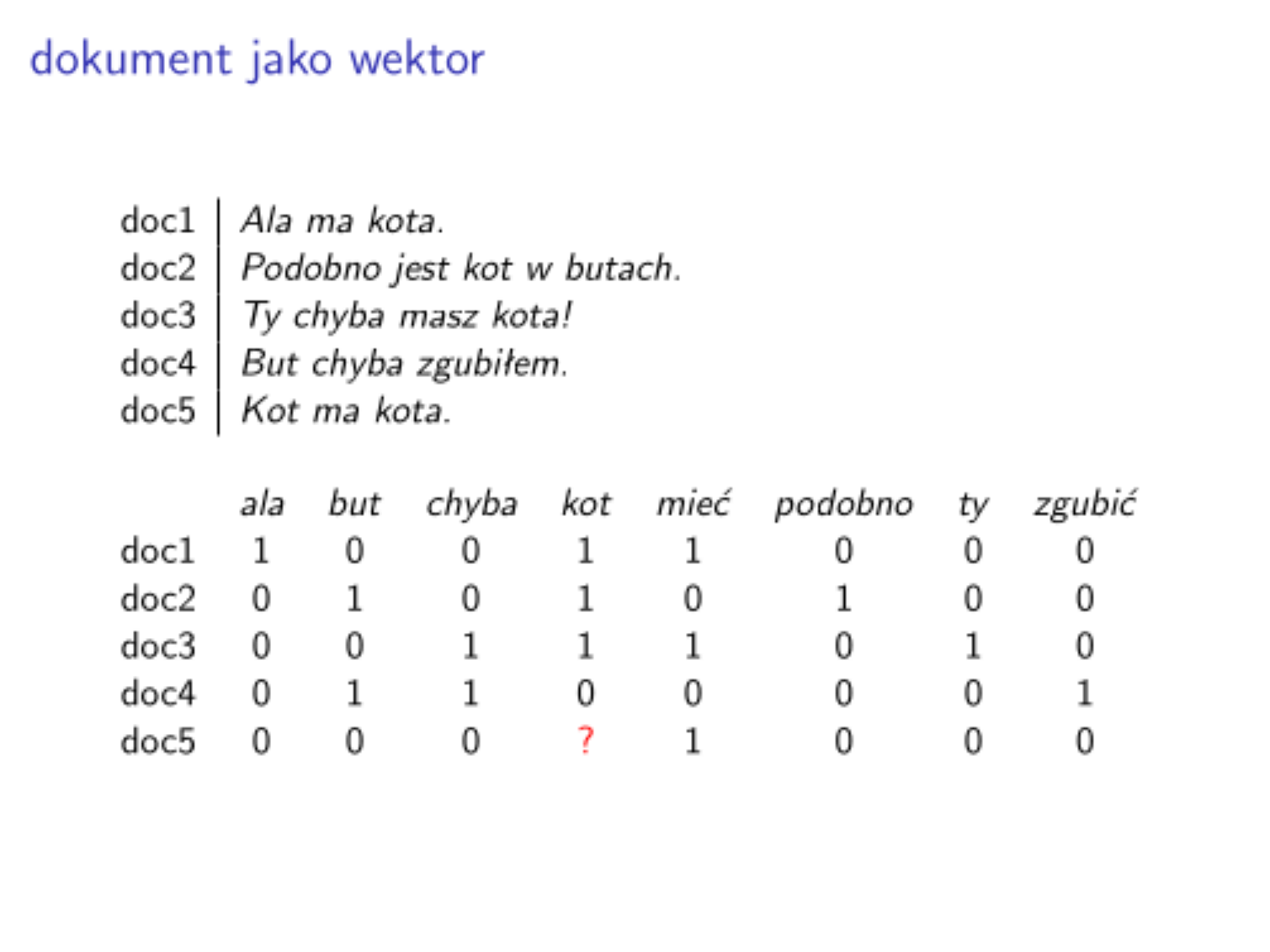
Roboczy przykład

Zakładamy, że mamy pewną kolekcję dokumentów $D = {d_1, \ldots, d_N}$. ($N$ - liczba dokumentów w kolekcji).

{-# LANGUAGE OverloadedStrings #-}

import Data.Text hiding(map, filter, zip)
import Prelude hiding(words, take)

collectionD :: [Text]
collectionD = ["Ala ma kota.", "Podobno jest kot w butach.", "Ty chyba masz kota!", "But chyba zgubiłem.", "Kot ma kota."]

-- Operator (!!) zwraca element listy o podanym indeksie
-- (Przy większych listach będzie nieefektywne, ale nie będziemy komplikować)
Prelude.head collectionD

Ala ma kota.

Wydobycie tekstu

Przykładowe narzędzia:

pdftotext
antiword
Tesseract OCR
Apache Tika - uniwersalne narzędzie do wydobywania tekstu z różnych formatów

Normalizacja tekstu

Cokolwiek robimy z tekstem, najpierw musimy go _znormalizować.

Tokenizacja

Po pierwsze musimy podzielić tekst na _tokeny, czyli wyrazapodobne jednostki. Może po prostu podzielić po spacjach?

tokenizeStupidly :: Text -> [Text]
-- words to funkcja z Data.Text, która dzieli po spacjach
tokenizeStupidly = words

tokenizeStupidly $ Prelude.head collectionD

Ala

ma

kota.

A, trzeba _chociaż odsunąć znaki interpunkcyjne. Najprościej użyć wyrażenia regularnego. Warto użyć unikodowych własności znaków i konstrukcji \p{...}.

{-# LANGUAGE QuasiQuotes #-}

import Text.Regex.PCRE.Heavy

tokenize :: Text -> [Text]
tokenize = map fst . scan [re|C\+\+|[\p{L}0-9]+|\p{P}|]

tokenize $ collectionD !! 3

But

chyba

zgubiłem

Cała kolekcja stokenizowana:

map tokenize collectionD

Ala

ma

kota

Podobno

jest

kot

butach

Ty

chyba

masz

kota

But

chyba

zgubiłem

Kot

ma

kota

Problemy z tokenizacją

Język angielski

tokenize "I use a data-base"

use

data

base

tokenize "I use a database"

use

database

tokenize "I use a data base"

use

data

base

tokenize "'I don't like Python'"

don

like

Python

tokenize "I can see the Johnes' house"

can

see

the

Johnes

house

tokenize "I do not like Python"

do

not

like

Python

tokenize "+0018 555-555-122"

tokenize "+0018555555122"

0018555555122

tokenize "Which one is better: C++ or C#?"

Which

one

is

better

C++

or

Inne języki?

tokenize "Rechtsschutzversicherungsgesellschaften wie die HUK-Coburg machen es bereits seit geraumer Zeit vor:"

Rechtsschutzversicherungsgesellschaften

wie

die

HUK

Coburg

machen

es

bereits

seit

geraumer

Zeit

vor

tokenize "今日波兹南是贸易、工业及教育的中心。波兹南是波兰第五大的城市及第四大的工业中心，波兹南亦是大波兰省的行政首府。也舉辦有不少展覽會。是波蘭西部重要的交通中心都市。"

今日波兹南是贸易

、

工业及教育的中心

。

波兹南是波兰第五大的城市及第四大的工业中心

，

波兹南亦是大波兰省的行政首府

。

也舉辦有不少展覽會

。

是波蘭西部重要的交通中心都市

。

tokenize "l'ordinateur"

ordinateur

Lematyzacja

_Lematyzacja to sprowadzenie do formy podstawowej (lematu), np. "krześle" do "krzesło", "zrobimy" do "zrobić" dla języka polskiego, "chairs" do "chair", "made" do "make" dla języka angielskiego.

Lematyzacja dla języka polskiego jest bardzo trudna, praktycznie nie sposób wykonać ją regułowo, po prostu musimy się postarać o bardzo obszerny _słownik form fleksyjnych.

Na potrzeby tego wykładu stwórzmy sobie mały słownik form fleksyjnych w postaci tablicy asocjacyjnej (haszującej).

import Data.Map as Map hiding(take, map, filter)

mockInflectionDictionary :: Map Text Text
mockInflectionDictionary = Map.fromList [
   ("kota", "kot"),
   ("butach", "but"),
   ("masz", "mieć"),
   ("ma", "mieć"),
   ("buta", "but"),
   ("zgubiłem", "zgubić")]

lemmatizeWord :: Map Text Text -> Text -> Text
lemmatizeWord dict w = findWithDefault w w dict

lemmatizeWord mockInflectionDictionary "butach"
-- a tego nie ma w naszym słowniczku, więc zwracamy to samo
lemmatizeWord mockInflectionDictionary "butami"

lemmatize :: Map Text Text -> [Text] -> [Text]
lemmatize dict = map (lemmatizeWord dict)

lemmatize mockInflectionDictionary $ tokenize $ collectionD !! 0 

lemmatize mockInflectionDictionary $ tokenize "Wczoraj kupiłem kota."

Use head

Found:

collectionD !! 0

Why Not:

head collectionD

but

butami

Ala

mieć

kot

Wczoraj

kupiłem

kot

Pytanie: Nawet w naszym słowniczku mamy problemy z niejednoznacznością lematyzacji. Jakie?

Obszerny słownik form fleksyjnych dla języka polskiego: http://zil.ipipan.waw.pl/PoliMorf?action=AttachFile&do=view&target=PoliMorf-0.6.7.tab.gz

Stemowanie

Stemowanie (rdzeniowanie) obcina wyraz do _rdzenia niekoniecznie będącego sensownym wyrazem, np. "krześle" może być rdzeniowane do "krześl", "krześ" albo "krzes", "zrobimy" do "zrobi".

stemowanie nie jest tak dobrze określone jak lematyzacja (można robić na wiele sposobów)
bardziej podatne na metody regułowe (choć dla polskiego i tak trudno)
dla angielskiego istnieją znane algorytmy stemowania, np. algorytm Portera
zob. też program Snowball z regułami dla wielu języków

Prosty stemmer "dla ubogich" dla języka polskiego to obcinanie do sześciu znaków.

poorMansStemming :: Text -> Text
poorMansStemming = Data.Text.take 6

poorMansStemming "zrobimy"
poorMansStemming "komputerami"
poorMansStemming "butach"
poorMansStemming "źdźbłami"

zrobim

komput

butach

źdźbła

_Stop words

Często wyszukiwarki pomijają krótkie, częste i nieniosące znaczenia słowa - _stop words (słowa przestankowe).

isStopWord :: Text -> Bool
isStopWord "w" = True
isStopWord "jest" = True
isStopWord "że" = True
-- przy okazji możemy pozbyć się znaków interpunkcyjnych
isStopWord w = w ≈ [re|^\p{P}+$|]

isStopWord "kot"
isStopWord "!"

False

True

removeStopWords :: [Text] -> [Text]
removeStopWords = filter (not . isStopWord)

removeStopWords $ tokenize $ Prelude.head collectionD

Ala

ma

kota

Pytanie: Jakim zapytaniom usuwanie _stop words może szkodzić? Podać przykłady dla języka polskiego i angielskiego.

Normalizacja - różności

W skład normalizacji może też wchodzić:

poprawianie błędów literowych
sprowadzanie do małych liter (lower-casing czy raczej case-folding)
usuwanie znaków diakrytycznych

toLower "ŻDŹBŁO"

żdźbło

toCaseFold "ŹDŹBŁO"

źdźbło

Pytanie: Kiedy _case-folding da inny wynik niż lower-casing? Jakie to ma praktyczne znaczenie?

Normalizacja jako całościowy proces

Najważniejsza zasada: dokumenty w naszej kolekcji powinny być normalizowane w dokładnie taki sposób, jak zapytania.

Efektem normalizacji jest zamiana dokumentu na ciąg _termów (ang. terms), czyli znormalizowanych wyrazów.

Innymi słowy po normalizacji dokument $d_i$ traktujemy jako ciąg termów $t_i^1,\dots,t_i^{|d_i|}$.

normalize :: Text -> [Text]
normalize = map poorMansStemming . removeStopWords . map toLower . lemmatize mockInflectionDictionary . tokenize

map normalize collectionD

ala

mieć

kot

podobn

kot

but

ty

chyba

mieć

kot

but

chyba

zgubić

kot

mieć

kot

Zbiór wszystkich termów w kolekcji dokumentów nazywamy słownikiem (ang. _vocabulary), nie mylić ze słownikiem jako strukturą danych w Pythonie (dictionary).

$$V = \bigcup_{i=1}^N \{t_i^1,\dots,t_i^{|d_i|}\}$$

(To zbiór, więc liczymy bez powtórzeń!)

import Data.Set as Set hiding(map)

getVocabulary :: [Text] -> Set Text 
getVocabulary = Set.unions . map (Set.fromList . normalize) 

getVocabulary collectionD

fromList ["ala","but","chyba","kot","mie\263","podobn","ty","zgubi\263"]

Jak wyszukiwarka może być szybka?

_Odwrócony indeks (ang. inverted index) pozwala wyszukiwarce szybko szukać w milionach dokumentów. Odwrócony indeks to prostu... indeks, jaki znamy z książek (mapowanie słów na numery stron/dokumentów).

collectionDNormalized = map normalize collectionD

documentToPostings :: ([Text], Int) -> Set (Text, Int)
documentToPostings (d, ix) = Set.fromList $ map (\t -> (t, ix)) d

documentToPostings (collectionDNormalized !! 2, 2)

Use tuple-section

Found:

\ t -> (t, ix)

Why Not:

(, ix)

fromList [("chyba",2),("kot",2),("mie\263",2),("ty",2)]

collectionToPostings :: [[Text]] -> Set (Text, Int)
collectionToPostings coll = Set.unions $ map documentToPostings $ Prelude.zip coll [0..]

collectionToPostings collectionDNormalized

Use zipWith

Found:

map documentToPostings $ Prelude.zip coll [0 .. ]

Why Not:

zipWith (curry documentToPostings) coll [0 .. ]

fromList [("ala",0),("but",1),("but",3),("chyba",2),("chyba",3),("kot",0),("kot",1),("kot",2),("kot",4),("mie\263",0),("mie\263",2),("mie\263",4),("podobn",1),("ty",2),("zgubi\263",3)]

updateInvertedIndex :: (Text, Int) -> Map Text [Int] -> Map Text [Int]
updateInvertedIndex (t, ix) invIndex = insertWith (++) t [ix] invIndex

getInvertedIndex :: [[Text]] -> Map Text [Int]
getInvertedIndex = Prelude.foldr updateInvertedIndex Map.empty . Set.toList . collectionToPostings

ind = getInvertedIndex collectionDNormalized
ind
ind ! "kot"

Eta reduce

Found:

updateInvertedIndex (t, ix) invIndex
  = insertWith (++) t [ix] invIndex

Why Not:

updateInvertedIndex (t, ix) = insertWith (++) t [ix]

fromList [("ala",[0]),("but",[1,3]),("chyba",[2,3]),("kot",[0,1,2,4]),("mie\263",[0,2,4]),("podobn",[1]),("ty",[2]),("zgubi\263",[3])]

[0,1,2,4]

Relewantność

Potrafimy szybko przeszukiwać znormalizowane dokumenty, ale które dokumenty są ważne (_relewantne) względem potrzeby informacyjnej użytkownika?

Zapytania boole'owskie

pizzeria Poznań dowóz to pizzeria AND Poznań AND dowóz czy pizzeria OR Poznań OR dowóz
`(pizzeria OR pizza OR tratoria) AND Poznań AND dowóz
pizzeria AND Poznań AND dowóz AND NOT golonka

Jak domyślnie interpretować zapytanie?

jako zapytanie AND -- być może za mało dokumentów
rozwiązanie pośrednie?
jako zapytanie OR -- być może za dużo dokumentów

Możemy jakieś miary dopasowania dokumentu do zapytania, żeby móc posortować dokumenty...

Mierzenie dopasowania dokumentu do zapytania

Potrzebujemy jakieś funkcji $\sigma : Q x D \rightarrow \mathbb{R}$.

Musimy jakoś zamienić dokumenty na liczby, tj. dokumenty na wektory liczb, a całą kolekcję na macierz.

Po pierwsze ponumerujmy wszystkie termy ze słownika.

voc = getVocabulary collectionD

vocD :: Map Int Text
vocD = Map.fromList $ zip [0..] $ Set.toList voc

invvocD :: Map Text Int
invvocD = Map.fromList $ zip (Set.toList voc) [0..]

vocD

invvocD

vocD ! 0
invvocD ! "chyba"

fromList [(0,"ala"),(1,"but"),(2,"chyba"),(3,"kot"),(4,"mie\263"),(5,"podobn"),(6,"ty"),(7,"zgubi\263")]

fromList [("ala",0),("but",1),("chyba",2),("kot",3),("mie\263",4),("podobn",5),("ty",6),("zgubi\263",7)]

ala

Napiszmy funkcję, która _wektoryzuje znormalizowany dokument.

vectorize :: Int -> Map Int Text -> [Text] -> [Double]
vectorize vecSize v doc = map (\i -> count (v ! i) doc) $ [0..(vecSize-1)]
   where count t doc 
           | t `elem` doc = 1.0
           | otherwise = 0.0
           
vocSize = Set.size voc

(collectionDNormalized !! 2)
vectorize vocSize vocD (collectionDNormalized !! 2)

Redundant $

Found:

map (\ i -> count (v ! i) doc) $ [0 .. (vecSize - 1)]

Why Not:

map (\ i -> count (v ! i) doc) [0 .. (vecSize - 1)]

Redundant bracket

Found:

(collectionDNormalized !! 2)

Why Not:

collectionDNormalized !! 2

ty

chyba

mieć

kot

[0.0,0.0,1.0,1.0,1.0,0.0,1.0,0.0]

Jak inaczej uwzględnić częstość wyrazów?

$ \newcommand{\idf}{\mathop{\rm idf}\nolimits} \newcommand{\tf}{\mathop{\rm tf}\nolimits} \newcommand{\df}{\mathop{\rm df}\nolimits} \newcommand{\tfidf}{\mathop{\rm tfidf}\nolimits} $

$\tf_{t,d}$ - term frequency
$1+\log(\tf_{t,d})$
$0.5 + \frac{0.5 \times \tf_{t,d}}{max_t(\tf_{t,d})}$

vectorizeTf :: Int -> Map Int Text -> [Text] -> [Double]
vectorizeTf vecSize v doc = map (\i -> count (v ! i) doc) $ [0..(vecSize-1)]
   where count t doc = fromIntegral $ (Prelude.length . Prelude.filter (== t)) doc

vocSize = Set.size voc

(collectionDNormalized !! 4)
vectorize vocSize vocD (collectionDNormalized !! 4)
vectorizeTf vocSize vocD (collectionDNormalized !! 4)

Redundant $

Found:

map (\ i -> count (v ! i) doc) $ [0 .. (vecSize - 1)]

Why Not:

map (\ i -> count (v ! i) doc) [0 .. (vecSize - 1)]

Redundant bracket

Found:

(collectionDNormalized !! 4)

Why Not:

collectionDNormalized !! 4

kot

mieć

kot

[0.0,0.0,0.0,1.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,2.0,1.0,0.0,0.0,0.0]

$ \newcommand{\idf}{\mathop{\rm idf}\nolimits} \newcommand{\tf}{\mathop{\rm tf}\nolimits} \newcommand{\df}{\mathop{\rm df}\nolimits} \newcommand{\tfidf}{\mathop{\rm tfidf}\nolimits} $

Odwrotna częstość dokumentowa

Czy wszystkie wyrazy są tak samo ważne?

NIE. Wyrazy pojawiające się w wielu dokumentach są mniej ważne.

Aby to uwzględnić, przemnażamy frekwencję wyrazu przez _odwrotną częstość w dokumentachinverse document frequency):

$$\idf_t = \log \frac{N}{\df_t},$$

gdzie:

$\idf_t$ - odwrotna częstość wyrazu $t$ w dokumentach
$N$ - liczba dokumentów w kolekcji
$\df_f$ - w ilu dokumentach wystąpił wyraz $t$?

Dlaczego idf?

term $t$ wystąpił...

w 1 dokumencie, $\idf_t = \log N/1 = \log N$
2 razy w kolekcji, $\idf_t = \log N/2$ lub $\log N$
w połowie dokumentów kolekcji, $\idf_t = \log N/(N/2) = \log 2$
we wszystkich dokumentach, $\idf_t = \log N/N = \log 1 = 0$

idf :: [[Text]] -> Text -> Double
idf coll t = log (fromIntegral n / fromIntegral df)
  where df = Prelude.length $ Prelude.filter (\d -> t `elem` d) coll
        n = Prelude.length coll
        
idf collectionDNormalized "kot"

0.22314355131420976

idf collectionDNormalized "chyba"

0.9162907318741551

Co z tego wynika?

Zamiast $\tf_{t,d}$ będziemy w wektorach rozpatrywać wartości:

$$\tfidf_{t,d} = \tf_{t,d} \times \idf_{t}$$

vectorizeTfIdf :: Int -> [[Text]] -> Map Int Text -> [Text] -> [Double]
vectorizeTfIdf vecSize coll v doc = map (\i -> count (v ! i) doc * idf coll (v ! i)) [0..(vecSize-1)]
   where count t doc = fromIntegral $ (Prelude.length . Prelude.filter (== t)) doc

vocSize = Set.size voc

collectionDNormalized !! 4
vectorize vocSize vocD (collectionDNormalized !! 4)
vectorizeTf vocSize vocD (collectionDNormalized !! 4)
vectorizeTfIdf vocSize collectionDNormalized vocD (collectionDNormalized !! 4)

kot

mieć

kot

[0.0,0.0,0.0,1.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,2.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,0.44628710262841953,0.5108256237659907,0.0,0.0,0.0]

map (vectorizeTfIdf vocSize collectionDNormalized vocD) collectionDNormalized

[[1.6094379124341003,0.0,0.0,0.22314355131420976,0.5108256237659907,0.0,0.0,0.0],[0.0,0.9162907318741551,0.0,0.22314355131420976,0.0,1.6094379124341003,0.0,0.0],[0.0,0.0,0.9162907318741551,0.22314355131420976,0.5108256237659907,0.0,1.6094379124341003,0.0],[0.0,0.9162907318741551,0.9162907318741551,0.0,0.0,0.0,0.0,1.6094379124341003],[0.0,0.0,0.0,0.44628710262841953,0.5108256237659907,0.0,0.0,0.0]]

Teraz zdefiniujemy _overlap score measure:

$$\sigma(q,d) = \sum_{t \in q} \tfidf_{t,d}$$

Podobieństwo kosinusowe

_Overlap score measure nie jest jedyną możliwą metryką, za pomocą której możemy mierzyć dopasowanie dokumentu do zapytania. Możemy również sięgnąć po intuicje geometryczne (skoro mamy do czynienia z wektorami).

Pytanie: Ile wymiarów mają wektory, na których operujemy? Jak "wyglądają" te wektory? Czy możemy wykonywać na nich standardowe operacje geometryczne czy te, które znamy z geometrii liniowej?

Podobieństwo między dokumentami

Zajmijmy się teraz poszukiwaniem miary mierzącej podobieństwo między dokumentami $d_1$ i $d_2$ (czyli poszukujemy sensownej funkcji $\sigma : D x D \rightarrow \mathbb{R}$).

Uwaga Pojęcia "miary" używamy nieformalnie, nie spełnia ona założeń znanych z teorii miary.

Rozpatrzmy zbiorek tekstów legend miejskich z git://gonito.net/polish-urban-legends.

(To autentyczne teksty z Internentu, z językiem potocznym, wulgarnym itd.)

   git clone git://gonito.net/polish-urban-legends
   paste polish-urban-legends/dev-0/expected.tsv polish-urban-legends/dev-0/in.tsv > legendy.txt

import System.IO
import Data.List.Split as SP

legendsh <- openFile "legendy.txt" ReadMode
hSetEncoding legendsh utf8
contents <- hGetContents legendsh
ls = Prelude.lines contents
items = map (map pack . SP.splitOn "\t") ls
Prelude.head items

na_ak

Opowieść prawdziwa... Olsztyn, akademik, 7 piętro, impreza u Mariusza, jak to na polskiej najebce bywa ktoś rzucił tekstem: "Mariusz nie zjedziesz na nartach po schodach". Sprawa ucichla, studencii wrocili do tego co lubia i w sumie umieją najbardziej czyli picia, lecz nad ranem kolo godziny 6.00 ludzia przypomnialo sie ze Mariusz miał zjechać na nartach po schodach. Tu warto wspomnieć że Mariusz był zapalonym narciarzem stąd właśnie w jego pokoju znalezc można bylo narty, bo po ki huj komuś narty w Olsztynie! Tak wracajac do historii nasz bohater odział się w sprzet, podszed do schodow i niestety dał radę zjechać jedynie w połowie, gdyż jak to powiedzial "no kurwa potknąłem sie", ale nieustraszoony Mariusz próbowal dalej. Nastepny zjazd byl perfekcyjny, jedno pietro zanim, niestety pomiedzy 6 a 5 pietrem Mariusza natrafil na Pania sprzątaczke, która potrącił i zwiał z miejsca wypadku. Ok godziny 10.00 nastopilo przebudzenie Mariusza, ktory zaraz po obudzeniu uslyszal co narobił, mianowicie o skutkach potracenia, Pani sprzataczka złamala rękę i trafiła do szpitala. Mogły powstać przez to cieżkie konsekwencje, Mariusz mógł wyleciec z akademika jeżeli kierownik dowie sie o calym zajściu. Wiec koledzy poradzili narciażowi, aby kupił kwiaty i bombonierkę i poszedł do szpitala z przeprosinami. Po szybkich zakupach w sasiedniej Biedrące, Mariusz byl przygotowany na konfrontacje z Pania sprzątaczka, ale nie mogło pojść pięknie i gładko. Po wejściu do szpitala nasz bohater skierowal swoje kroki do recepcji pytajac się o ciocię, która miała wypadek w akademiku, recepcjonistka skierowała go do lekarza, gdzie czekał na jego wyjście ok 15 minut, gdy lekarz już wyszedł ten odrazu podleciał do niego, żeby spytać się o stan zdrowia Pani sprzątaczki. Wnet uslyszla od lekarz, niestety Pani teraz jest u psychiatry po twierdzi, że ktoś potracil ja zjeżdzajac na nartach w akademiku. Po uslyszeniu tej wiadomosci Mariusz odwrocił się, wybiegł, kupił piecie i szybko pobiegł do akademika pić dalej! Morał... student potrafi!

nbOfLegends = Prelude.length items
nbOfLegends

labelsL = map Prelude.head items
labelsL
collectionL = map (!!1) items
items !! 1

na_ak

w_lud

ba_hy

w_lap

ne_dz

be_wy

zw_oz

mo_zu

be_wy

ba_hy

mo_zu

be_wy

w_lud

ne_dz

ta_ab

ta_ab

ta_ab

w_lap

ba_hy

ne_dz

ba_hy

tr_su

ne_dz

ba_hy

mo_zu

tr_su

zw_oz

ne_dz

ne_dz

w_lud

zw_oz

zw_oz

zw_oz

ne_dz

ta_ab

zw_oz

w_lud

na_ak

zw_oz

w_lap

be_wy

na_ak

zw_oz

w_lap

na_ak

ba_hy

zw_oz

w_lud

zw_oz

zw_oz

mo_zu

ba_hy

zw_oz

tr_su

na_ak

ba_hy

w_lud

w_lud

zw_oz

tr_su

zw_oz

w_lud

zw_oz

zw_oz

be_wy

tr_su

zw_oz

na_ak

ba_hy

zw_oz

ne_dz

ba_hy

na_ak

zw_oz

w_lud

mo_zu

mo_zu

na_ak

w_lap

ne_dz

ba_hy

mo_zu

ba_hy

ne_dz

zw_oz

tr_su

ne_dz

w_lud

Ja podejrzewam że o polowaniu nie było mowy, po prostu znalazł martwego szczupaka i skorzystał z okazji! Mnie mocno zdziwiła jego siła żeby taki pół kilogramowy okaz szczupaka przesuwać o parę metrów i to w trzcinach! Szacuneczek. Przypomniala mi sie historia którą kiedys zaslyszalem o wlascicielce pytona, ktory nagle polozyl sie wzdluz jej łóżka. Leżał tak wyciągniety jak struna dłuższy czas jak nieżywy (a był długości łóżka), więc kobitka zadzonila do weterynarza co ma robić. Usłyszała że ma szybko zamknąć się w łazience i poczekać na niego bo pyton ją mierzy jako potencjalną ofiarę (czy mu się zmieści w brzuchu...). Wierzyć, nie wierzyć? Kiedyś nie wierzyłem ale od kilku dni mam wątpliwosci... Pozdrawiam

collectionLNormalized = map normalize collectionL
voc' = getVocabulary collectionL

vocLSize = Prelude.length voc'

vocL :: Map Int Text
vocL = Map.fromList $ zip [0..] $ Set.toList voc'

invvocL :: Map Text Int
invvocL = Map.fromList $ zip (Set.toList voc') [0..]

vocL ! 0
invvocL ! "chyba"

Wektoryzujemy całą kolekcję:

lVectorized = map (vectorizeTfIdf vocLSize collectionLNormalized vocL) collectionLNormalized
lVectorized !! 1

[0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.38837067474886433,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.752336051950276,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0647107369924282,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2078115806331018,0.0,0.0,0.0,0.0,0.0,1.247032293786383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.5947071077466928,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.268683541318364,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2078115806331018,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.7578579175523736,0.0,0.0,0.0,0.0,0.0,0.3550342544812725,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.9395475940384223,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.21437689194643514,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2878542883066382,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2745334443309775,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,1.247032293786383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.386466576974748,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,1.0319209141694374,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,2.340142505300509,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.7578579175523736,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.5214691394881432,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,8.388148398070203e-2,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.9810014688665833,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.6096847248398047,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.575536360758419,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.1847155011136463,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0319209141694374,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.322773392263051,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.900958761193047,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,3.079613757534693,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.340142505300509,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.710068508962545,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,8.931816237309167,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0319209141694374,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.26121549926361765,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.386466576974748,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,9.238841272604079,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.12210269680089991,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.068012845856213,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,5.712940412440966,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.068012845856213,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]

Szukamy funkcji $sigma$, która da wysoką wartość dla tekstów dotyczących tego samego wątku legendowego (np. $d_1$ i $d_2$ mówią o wężu przymierzającym się do zjedzenia swojej właścicielki) i niską dla tekstów z różnych wątków (np. $d_1$ opowiada o wężu ludojadzie, $d_2$ - bałwanku na hydrancie).

Może po prostu odległość euklidesowa, skoro to punkty w wielowymiarowej przestrzeni?

import Text.Printf
import Data.List (take)

formatNumber :: Double -> String
formatNumber x = printf "% 7.2f" x

similarTo :: ([Double] -> [Double] -> Double) -> [[Double]] -> Int -> Text
similarTo simFun vs ix = pack $ Prelude.unwords $ map (formatNumber . ((vs !! ix) `simFun`)) vs

euclDistance :: [Double] -> [Double] -> Double
euclDistance v1 v2 = sqrt $ sum $ Prelude.zipWith (\x1 x2 -> (x1 - x2)**2) v1 v2

limit = 13
labelsLimited =  Data.List.take limit labelsL
limitedL = Data.List.take limit lVectorized

similarTo euclDistance limitedL 0

Eta reduce

Found:

formatNumber x = printf "% 7.2f" x

Why Not:

formatNumber = printf "% 7.2f"

   0.00   79.93   78.37   76.57   87.95   81.15   82.77  127.50  124.54   76.42   84.19   78.90   90.90

paintMatrix :: ([Double] -> [Double] -> Double) -> [Text] -> [[Double]] -> Text
paintMatrix simFun labels vs = header <> "\n" <> (Data.Text.unlines $ map (\(lab, ix) -> lab <> " " <> similarTo simFun vs ix) $ zip labels [0..(Prelude.length vs - 1)])
    where header = "      " <> (Data.Text.unwords $ map (\l -> pack $ printf "% 7s" l) labels)
    
paintMatrix euclDistance labelsLimited limitedL

Move brackets to avoid $

Found:

"\n"
  <>
    (Data.Text.unlines
       $ map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
           $ zip labels [0 .. (Prelude.length vs - 1)])

Why Not:

"\n"
  <>
    Data.Text.unlines
      (map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
         $ zip labels [0 .. (Prelude.length vs - 1)])

Use zipWith

Found:

map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
  $ zip labels [0 .. (Prelude.length vs - 1)]

Why Not:

zipWith
  (curry (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix))
  labels [0 .. (Prelude.length vs - 1)]

Move brackets to avoid $

Found:

"      "
  <> (Data.Text.unwords $ map (\ l -> pack $ printf "% 7s" l) labels)

Why Not:

"      "
  <> Data.Text.unwords (map (\ l -> pack $ printf "% 7s" l) labels)

Avoid lambda

Found:

\ l -> pack $ printf "% 7s" l

Why Not:

pack . printf "% 7s"

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak    0.00   79.93   78.37   76.57   87.95   81.15   82.77  127.50  124.54   76.42   84.19   78.90   90.90
w_lud   79.93    0.00   38.92   34.35   56.48   44.89   47.21  109.24  104.82   35.33   49.88   39.98   60.20
ba_hy   78.37   38.92    0.00   30.37   54.23   40.93   43.83  108.15  102.91   27.37   46.95   35.81   58.99
w_lap   76.57   34.35   30.37    0.00   51.54   37.46   40.86  107.43  103.22   25.22   43.66   32.10   56.53
ne_dz   87.95   56.48   54.23   51.54    0.00   57.98   60.32  113.66  109.59   50.96   62.17   54.84   70.70
be_wy   81.15   44.89   40.93   37.46   57.98    0.00   49.55  110.37  100.50   37.77   51.54   37.09   62.92
zw_oz   82.77   47.21   43.83   40.86   60.32   49.55    0.00  111.11  107.57   41.02   54.07   45.23   64.65
mo_zu  127.50  109.24  108.15  107.43  113.66  110.37  111.11    0.00  139.57  107.38  109.91  108.20  117.07
be_wy  124.54  104.82  102.91  103.22  109.59  100.50  107.57  139.57    0.00  102.69  108.32   99.06  113.25
ba_hy   76.42   35.33   27.37   25.22   50.96   37.77   41.02  107.38  102.69    0.00   43.83   32.08   56.68
mo_zu   84.19   49.88   46.95   43.66   62.17   51.54   54.07  109.91  108.32   43.83    0.00   47.87   66.40
be_wy   78.90   39.98   35.81   32.10   54.84   37.09   45.23  108.20   99.06   32.08   47.87    0.00   59.66
w_lud   90.90   60.20   58.99   56.53   70.70   62.92   64.65  117.07  113.25   56.68   66.40   59.66    0.00

Problem: za dużo zależy od długości tekstu.

Rozwiązanie: znormalizować wektor $v$ do wektora jednostkowego.

$$ \vec{1}(v) = \frac{v}{|v|} $$

Taki wektor ma długość 1!

vectorNorm :: [Double] -> Double
vectorNorm vs = sqrt $ sum $ map (\x -> x * x) vs

toUnitVector :: [Double] -> [Double]
toUnitVector vs = map (/ n) vs
   where n = vectorNorm vs

vectorNorm (toUnitVector [3.0, 4.0])

euclDistanceNormalized :: [Double] -> [Double] -> Double
euclDistanceNormalized v1 v2 = toUnitVector v1 `euclDistance` toUnitVector v2

euclSim v1 v2 = 1 / (d + 0.1)
   where d = euclDistanceNormalized v1 v2

paintMatrix euclSim labelsLimited limitedL

1.0

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak   10.00    0.67    0.66    0.66    0.67    0.67    0.67    0.67    0.67    0.67    0.66    0.67    0.67
w_lud    0.67   10.00    0.67    0.68    0.67    0.66    0.67    0.67    0.68    0.66    0.67    0.67    0.68
ba_hy    0.66    0.67   10.00    0.66    0.67    0.67    0.67    0.67    0.69    0.74    0.66    0.67    0.66
w_lap    0.66    0.68    0.66   10.00    0.66    0.66    0.66    0.66    0.67    0.66    0.66    0.66    0.66
ne_dz    0.67    0.67    0.67    0.66   10.00    0.67    0.67    0.68    0.69    0.68    0.67    0.67    0.68
be_wy    0.67    0.66    0.67    0.66    0.67   10.00    0.66    0.67    0.74    0.66    0.67    0.76    0.66
zw_oz    0.67    0.67    0.67    0.66    0.67    0.66   10.00    0.67    0.67    0.66    0.66    0.67    0.67
mo_zu    0.67    0.67    0.67    0.66    0.68    0.67    0.67   10.00    0.69    0.67    0.69    0.68    0.67
be_wy    0.67    0.68    0.69    0.67    0.69    0.74    0.67    0.69   10.00    0.68    0.67    0.75    0.67
ba_hy    0.67    0.66    0.74    0.66    0.68    0.66    0.66    0.67    0.68   10.00    0.66    0.67    0.66
mo_zu    0.66    0.67    0.66    0.66    0.67    0.67    0.66    0.69    0.67    0.66   10.00    0.67    0.67
be_wy    0.67    0.67    0.67    0.66    0.67    0.76    0.67    0.68    0.75    0.67    0.67   10.00    0.67
w_lud    0.67    0.68    0.66    0.66    0.68    0.66    0.67    0.67    0.67    0.66    0.67    0.67   10.00

Podobieństwo kosinusowe

Częściej zamiast odległości euklidesowej stosuje się podobieństwo kosinusowe, czyli kosinus kąta między wektorami.

Wektor dokumentu ($\vec{V}(d)$) - wektor, którego składowe odpowiadają wyrazom.

$$\sigma(d_1,d_2) = \cos\theta(\vec{V}(d_1),\vec{V}(d_2)) = \frac{\vec{V}(d_1) \cdot \vec{V}(d_2)}{|\vec{V}(d_1)||\vec{V}(d_2)|} $$

Zauważmy, że jest to iloczyn skalarny znormalizowanych wektorów!

$$\sigma(d_1,d_2) = \vec{1}(\vec{V}(d_1)) \times \vec{1}(\vec{V}(d_2)) $$

(✕) :: [Double] -> [Double] -> Double
(✕) v1 v2 = sum $ Prelude.zipWith (*) v1 v2

[2, 1, 0] ✕ [-2, 5, 10]

1.0

cosineSim v1 v2 = toUnitVector v1 ✕ toUnitVector v2

paintMatrix cosineSim labelsLimited limitedL

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak    1.00    0.02    0.01    0.01    0.03    0.02    0.02    0.04    0.03    0.02    0.01    0.02    0.03
w_lud    0.02    1.00    0.02    0.05    0.04    0.01    0.03    0.04    0.06    0.01    0.02    0.03    0.06
ba_hy    0.01    0.02    1.00    0.01    0.02    0.03    0.03    0.04    0.08    0.22    0.01    0.04    0.01
w_lap    0.01    0.05    0.01    1.00    0.01    0.01    0.00    0.01    0.02    0.00    0.00    0.00    0.00
ne_dz    0.03    0.04    0.02    0.01    1.00    0.04    0.03    0.07    0.08    0.06    0.03    0.03    0.05
be_wy    0.02    0.01    0.03    0.01    0.04    1.00    0.01    0.03    0.21    0.01    0.02    0.25    0.01
zw_oz    0.02    0.03    0.03    0.00    0.03    0.01    1.00    0.04    0.03    0.00    0.01    0.02    0.02
mo_zu    0.04    0.04    0.04    0.01    0.07    0.03    0.04    1.00    0.10    0.02    0.09    0.05    0.04
be_wy    0.03    0.06    0.08    0.02    0.08    0.21    0.03    0.10    1.00    0.05    0.03    0.24    0.04
ba_hy    0.02    0.01    0.22    0.00    0.06    0.01    0.00    0.02    0.05    1.00    0.01    0.02    0.00
mo_zu    0.01    0.02    0.01    0.00    0.03    0.02    0.01    0.09    0.03    0.01    1.00    0.01    0.02
be_wy    0.02    0.03    0.04    0.00    0.03    0.25    0.02    0.05    0.24    0.02    0.01    1.00    0.02
w_lud    0.03    0.06    0.01    0.00    0.05    0.01    0.02    0.04    0.04    0.00    0.02    0.02    1.00

collectionL !! 5

na tylnym siedzeniu w autobusie siedzi matka z 7-8 letnim synkiem. naprzeciwko synka siedzi kobieta (zwrócona twarzą do dzieciaka). synek co chwile wymachuje nogami i kopie kobietę, matka widząc to nie reaguje na to wogóle. wreszcie kobieta zwraca uwagę matce, żeby ta powiedziała coś synowi a matka do niej: nie mogę, bo wychowuję syna bezstresowo!!! ...chłopak, który stał w pobliżu i widział i słyszał całe to zajście wypluł z ust gumę do żucia i przykleił matce na czoło i powiedział: ja też byłem bezstresowo wychowywany... autentyczny przypadek w londyńskim autobusie (a tym co przykleił matce gumę na czoło był chyba nawet młody Polak)

collectionL !! 8

Krótko zwięźle i na temat. Zastanawia mnie jak ludzie wychowują dzieci. Co prawda sam nie mam potomstwa i nie zamierzam mieć jak narazie (bo to trochę głupie mieć 17-letniego tatusia), ale niestety mam przyjemność oglądać efekty wychowawcze niektórych par (dzięki znajomym rodziców w różnym wieku). Są trzy najbardziej znane mi modele wychowania. Surowe, bezstresowe (w moim znaczeniu) i "bezstresowe" w mowie potocznej. Zaczynam od tego pierwszego. Jak nazwa wskazuje, jest to surowe wychowanie, oparte na karach cielesnych lub torturach umysłowych. Nie uważam tego za dobre wychowanie, bo dziecko jak będzie nieco starsze będzie się bało wszystkiego, bo uzna, ż jak zrobi coś żle to spotka je kara. Więc bicie za różne rzeczy odpada (no chyba, że dzieciak na serio nabroi to oczywiście). Wychowanie bezstresowe z mojego słownika oznacza nienarażanie dziecka na stresy, pocieszanie w trudnych sytuacjach, załatwianie problemów przez rozmowę oraz stały kontakt z dzieckiem. I to chyba najlepsze. Sam zostałem tak wychowany i cieszę się z tego powodu. I oczywiście "wychowanie bezstresowe". A tu się normalnie rozpiszę. Po pierwsze geneza. Więc jak dochodzi do takiego wychowania? Odpowiedź. Mamusi i tatusiowi się zachciało bobaska bo to takie malutkie fajniutkie i ooo. Oboje zazdroszczą innym parom bo one mają, a oni nie, więc oni też chcą. No więc rodzi im się bobasek, chuchają dmuchają na niego póki małe. Ale przychodzi ten okres, kiedy dziecko trzeba wychować i kiedy ma się na dzieciaka największy wpływ. I tu się zaczynają schody. Nagle oboje nie mają czasu i mówią "Wychowamy go/ją/ich (niepotrzebne skreślić) bezstresowo." Po drugie. Decyzja o sposobie wychowania podjęta. A więc jak to wygląda? Odpowiedź. Totalna olewka! Mama i tata balują, a dzieciaka zostawiają samemu sobie, albo pod opiekę babci, która również leje na dziecko ciepłym moczem. Dzieciak rośnie i rośnie, nie wie co dobre a co złe. Przypomniała mi się pewna, podobno autentyczna scenka. Chłopak jedzie ze szwagrem autobusem czy tam tramwajem. Na jednym miejscu siedzi starowinka, a na przeciwko niej siedzi lafirynda z brzdącem na kolanach. No i sobie dzieciak macha nóżkami i tu ciach i kopnął staruszkę w nogę. Babcia nic sobie z tego nie zrobiła, a dzieciak nie widząc reakcji zaczął ją już celowo kopać. Staruszka: Może pani powiedzieć coś synkowi żeby mnie nie kopał. Matka: Nie bo ja go wychowuję bezstresowo. Szwagier wyciąga z ust gumę do żucia i przykleja mamusi na czoło mówiąc: Moja mama też mnie wychowała bezstresowo. Ciekaw jestem ile w tym prawdy było, a jeżeli 100% to czy mamusi się odmieniły poglądy. Kto go wie? Po trzecie. Dorosły wychowany bezstresowo. Jaki on jest? Odpowiedź. Zupełnie inny. Myśli, że jest pępkiem świata i że wszystko musi być pod jego dyktando. Pracując w Szwajcarii przy pielęgnacji winogron, syn polskiego kolegi taty zaczął rzucać we mnie winogronami. Miałem ochotę wbić mu nożyczki (którymi podcinałem liście) w oczy. A to byłby ciekawy widok. Dzieciak o białych włosach, skórze i niebieskich oczach stałby sie albinosem (bo z niebieskich oczu stałyby sie czerwone jak u białych szczurów i myszek). Ojciec sie co prawda na niego wydzierał, żeby nie przeszkadzał, ale jak widać dzieciak miał to po prostu w dupie. Więc skoro dziecko nie słucha się nawet rodzica, to jak w szkole posłucha nauczyciela? Jak znajdzie pracę, w której będzie jakiś szef (chyba, że sam sobie będzie szefem)? W ten oto sposób jak dowiaduję się o tym, że ktoś wychowuje dzieciaka bezstresowo, ciary przechodzą mi po plecach, a tegoż rodzica mam ochotę palnąć mu w łeb tak żeby się przekręcił (zarówno łeb jak i poglądy). A jak mnie wychowano? Byłem często sam sobie zostawiany. Ale nie oznacza że to byla wspomniana olewka. Jako, że rodzice pracowali, a rodzeństwo chodziło do szkoły, podrzucali mnie do babci. A wieczorami się mną opiekowali. Gadali jak miałem problemy i nie bili bo ponoć byłem spokojnym dzieckiem. No i tyle. Do 17 urodzin 2 dni, a szczura chyba nie dostanę. A sam nie kupię!;(

Z powrotem do wyszukiwarek

Możemy potraktować zapytanie jako bardzo krótki dokument, dokonać jego wektoryzacji i policzyć cosinus kąta między zapytaniem a dokumentem.

import Data.Ord
import Data.List

legendVectorizer = vectorizeTfIdf vocLSize collectionLNormalized vocL . normalize


query vs vzer q = map ((collectionL !!) . snd) $ Data.List.take 3 $ sortBy (\a b -> fst b `compare` fst a) $ zip (map (`cosineSim` qvec) vs) [0..]  
   where qvec = vzer q 

query lVectorized legendVectorizer "wąż przymierza się do zjedzenia właścicielki"

ja za to znam przypadek, że koleżanka mieszkala w bloku parę lat temu, pewnego razu wchodzi do łazienki w samej bieliźnie a tam ogromny wąż na podłodze i tak się wystraszyła że wybiegła z wrzaskiem z mieszkania i wyleciała przed blok w samej bieliźnie i uciekła do babci swojej, która mieszkala gdzieś niedaleko. a potem się okazało, że jej sąsiad z dołu hodował sobie węża i tak właśnie swobodnie go "pasał" po mieszkaniu i wąż mu spierdzielił przez rurę w łazience :cool :

Pewna dziewczyna, wieku mi nieznanego, w mieście stołecznym - rozwiodła się. Była sama i samotna, więc zapragnęła kupić sobie zwierzę, aby swą miłą obecnością rozjaśniało jej puste wieczory i takież poranki. Dziewczyna była najwyraźniej ekscentryczką, bo zamiast rozkosznego, miękkiego kociaka z czerwonym kłębuszkiem wełenki lub kudłatego pieska , co sika na parkiet i gryzie skarpetki - kupiła sobie ... węża. Wąż zamieszkał z dziewczyną, i dobrze im było. Gad jadł, spał i rósł, a po pierwszym okresie obojętności ( zwłaszcza ze strony węża ) nawiązała się między nimi nić porozumienia. Przynajmniej dziewczyna odczuwała tę nić wyraźnie, gdyż wąż reagował na jej obecność, a nocą spał zwinięty w kłębek w nogach jej łóżka. Po dwóch latach wspólnego bytowania, nie przerywanych żadnym znaczącym wydarzeniem w ich wzajemnych relacjach, dziewczyna zauważyła, że wąż stał się osowiały. Przestał jeść, chował się po kątach, a nocami, zamiast w nogach łóżka - sypiał wyciągnięty wzdłuż jej boku. Martwiła się o swojego gada i poszła z nim do weterynarza. Weterynarz zbadał go, zapisał leki na poprawę apetytu ( ciekawe, jak się bada węża ? ) i odesłał do domu. Zdrowie śliskiego pacjenta nie poprawiło się, więc troskliwa dziewczyna postanowiła zasięgnąć porady u znawcy gadów i gadzich obyczajów. Znawca wysłuchał opisu niepokojących objawów, i powiedział : - Proszę pani. Ten wąż nie jest chory. On teraz pości. A leży wzdłuż pani nocą, bo sprawdza, czy pani się zmieści. To prawdziwa historia. Opowiedziała nam ją dziś klientka. Leżę na łóżku, pisze tego posta, i patrzę na drzemiącą obok mnie kotkę. Trochę mała jest. Raczej nie ma szans, żebym sie zmieściła, jakby co..

Anakonda. Czy to kolejna miejska legenda? Jakiś czas temu koleżanka na jednej z imprez towarzyskich opowiedziała mrożącą krew w żyłach historię o dziewczynie ze swojej pracy, która w Warszawie na dyskotece w Dekadzie poznała chłopaka. Spotykała się z nim na kawę i po drugiej randce doszło do pocałunków. Umówiła się na trzecią randkę, ale zanim do niej doszło wyskoczył jej jakiś pryszcz na twarzy. Poszła do lekarza, a ten... zawiadomił policję, prokuraturę itd. , bo rozpoznał zarażenie... jadem trupim! Rozpoczęto przesłuchanie dziewczyny i po wyjaśnieniach trafiono do chłopaka, z którym się całowała. W jego domu odkryto rozkładające się zwłoki dwóch dziewczyn. Byłam ta historią wstrząśnięta. Następnego dnia opowiedziałam ją w pracy, a koleżanka Justyna przyznała, że już o tym slyszała. To mnie utwierdziło, że historia jest prawdziwa, ale... tylko do wieczora. Coś mi nie dawało spokoju. Uwaga TVN nic? Interwencja Polsatu - nic? Nasz rodzimy Telekurier nic? Zaczęłam sprawdzać w internecie co to jest jad trupi, opryszczka od zakażenia tymże jadem i tak... trafiłam na miejską legendę. Historia wydarzyła się nie tylko w Warszawie, ale i w Olsztynie, Toruniu, Wrocławiu i Krakowie, a być może w ogóle za granicą. Choć prawdopodobne jest, że nie wydarzyła się nigdy. Głośno o niej było na miejskch forach. Za każdym razem ofiara była czyjąś znajomą. Po przeczytaniu kolejnej wersji historii zadzwoniłam do koleżanki, która opowiedziała mi tę historię i sklęłam czym świat stoi. Dlatego kiedy kilka dni temu inna koleżanka opowiedziała kolejną mrożącą krew w żyłach historię - tym razem o anakondzie - rozpoczęłam poszukiwania w internecie czy to nie jest następna miejska legenda. Nic nie znalazłam. Jednak coś mi nie pasuje, choć ta historia może brzmieć wielce prawdopodobnie. Zwłaszcza, gdy ktoś oglądał głupawy film z J. Lo. Zainteresowało mnie to, bo siedząc nad powieścią "Dzika" poczytałam trochę o wężach. A o jaką historię mi chodzi? Pewna kobieta (podobno sąsiadka tej mojej koleżanki z pracy, która historię opowiadała) hodowała w domu węża - anakondę. Hodowała ją pięć lat i nie trzymała w terrarium. Anakonda chodziła (pełzała) samopas po domu i co kilka dni dostawała chomika, szczura, mysz lub królika do zjedzenia. Pewnego dnia przestała jeść i zaczęła się dziwnie zachowywać. Każdego ranka po przebudzeniu właścicielka znajdowała ją w swoim łóżku wyprostowaną jak struna. Po dwóch tygodniach takich zachowań ze strony anakondy właścicielka zaniepokojona stanem zdrowia ukochanego węża poszła z nim do lekarza. Ten wysłuchał objawów "choroby" i powiedział, że anakonda głodziła się, by zjeść... włascicielkę. Kładzenie się koło niej było mierzeniem ile jeszcze głodzić się trzeba, by właścicielka zmieściła się w pysku no i badaniem od której strony trzeba ją zaatakować. Wężowi chodziło bowiem o to, by smakowity i duży obiad się za bardzo nie bronił. Ja domyśliłam się od razu do czego zmierza ta historia (lektura artykułów o wężach zrobiła swoje), ale dla reszty, którzy słuchali było to szokiem. Mnie szokuje co innego. Po co trzymać węża skoro nie ma z nim człowiek żadnego kontaktu? To nie pies, kot czy inny ssak. To nie ptak. Wąż to wąż! Nie przyjdzie na zawołanie. Jaby ktoś nie wiedział to... Węże są mięsożerne. Połykają ofiary w całości, mimo że często wielokrotnie są one większe od samego węża. Połykanie polega na nasuwaniu się węża na swoją ofiarę. A anakonda... żyje zwykle w wodzie i na drzewach, żywiąc się ssakami (m.in. tapiry, dziki, kapibary, jelenie!, gryzonie, niekiedy nawet jaguary), gadami (kajmany), rybami i ptakami, polując zazwyczaj w nocy. Jest w stanie połknąć ofiarę znacznie szerszą od swojego ciała, co jest możliwe dzięki rozciągnięciu szczęk. Trawienie jest bardzo powolne - po posiłku wąż trawi większą ofiarę przez wiele dni, a potem może pościć przez szereg tygodni lub miesięcy. Zanotowany rekord postu, w przypadku anakondy znajdującej się w niewoli, wynosi 2 lata. Z historii wynika, że gdyby nie interwencja u weterynarza mogłaby rodzina przez kilka lat szukać właścicielki anakondy. Myśleliby, że jest na wycieczce a ona w brzuszku w postaci obiadku. Jest tylko jedno ale. Nigdzie nie znalazłam jednak śladu, ani nawet wzmianki o tym, że anakonda zjadła człowieka. I dlatego ciągle w sumie mam wątpliwości. ps. Dalszy los anakondy "sąsiadki" koleżanki nie jest mi znany.

134 KiB Raw Blame History Unescape Escape

Wyszukiwarka - szybka i sensowna

Roboczy przykład

Wydobycie tekstu

Normalizacja tekstu

Tokenizacja

Problemy z tokenizacją

Język angielski

Inne języki?

Lematyzacja

Stemowanie

_Stop words

Normalizacja - różności

Normalizacja jako całościowy proces

Jak wyszukiwarka może być szybka?

Relewantność

Zapytania boole'owskie

Mierzenie dopasowania dokumentu do zapytania

Jak inaczej uwzględnić częstość wyrazów?

Odwrotna częstość dokumentowa

Dlaczego idf?

Co z tego wynika?

Podobieństwo kosinusowe

Podobieństwo między dokumentami

Podobieństwo kosinusowe

Z powrotem do wyszukiwarek

134 KiB

Raw Blame History