5.7 KiB
Przygotowali
Wojciech Jarmosz
Michał Kubiak
Przemysław Owczarczyk
Temat:
Klasyfikacja za pomocą naiwnej metody bayesowskiej (rozkłady dyskretne). Implementacja powinna założyć, że cechy są dyskretne/jakościowe. Na wejściu oczekiwany jest zbiór, który zawiera p-cech dyskretnych/jakościowych, wektor etykiet oraz wektor prawdopodobieństw a priori dla klas. Na wyjściu otrzymujemy prognozowane etykiety oraz prawdopodobieństwa a posteriori. Dodatkową wartością odpowiednia wizualizacja.
Wstęp
Jednym z najbardziej użytecznych zastosowań twierdzenia Bayesa jest tzw. naiwny klasyfikator bayesowski - Prosty klasyfikator probabilistyczny. Naiwne klasyfikatory bayesowskie są oparte na założeniu o wzajemnej niezależności predyktorów (zmiennych niezależnych). Często nie mają one żadnego związku z rzeczywistością i właśnie z tego powodu nazywa się je naiwnymi. Klasyfikator ten można wykorzystywać do określania prawdopodobieństwa klas na podstawie szeregu różnych obserwacji.
Pomimo swojego naiwnego charakteru naiwna metoda bayesowska zwykle dobrze się sprawdza w praktyce. Jest to odpowiedni przykład obrazujący, co oznacza popularne w statystyce powiedzenie „wszystkie modele są złe, ale niektóre są użyteczne” (za autora tego powiedzenia uznaje się na ogół statystyka George'a E.P. Boxa).
Założenie naiwnego bayesa
$P(class | variable1, variable2, variable3) = \frac{P(variable1, variable2, valriable3|class) * P(class)}{P(variable1, variable2, variable3)}$
przy założeniu o niezależności zmiennych losowych $variable1$, $variable2$, $variable3$:
$P(variable1, variable2, variable3|class) = P(variable1|class)* P(variable2|class) * P(variable3|class)$
ostatecznie:
$P(class | variable1, variable2, variable3) = \frac{P(variable1|class)* P(variable2|class) * P(variable3|class) * P(class)}{\sum_k{P(variable1|class_k)* P(variable2|class_k) * P(variable3|class_k) * P(class_k)}}$
DataSet
Według Światowej Organizacji Zdrowia (WHO) udar to druga najczęstsza przyczyna zgonów na świecie, odpowiedzialna za około 11% wszystkich zgonów. Ten zestaw danych jest używany do przewidywania, czy pacjent prawdopodobnie dostanie udaru, na podstawie parametrów wejściowych, takich jak płeć, wiek, różne choroby. https://www.kaggle.com/fedesoriano/stroke-prediction-dataset
Wizualizacja
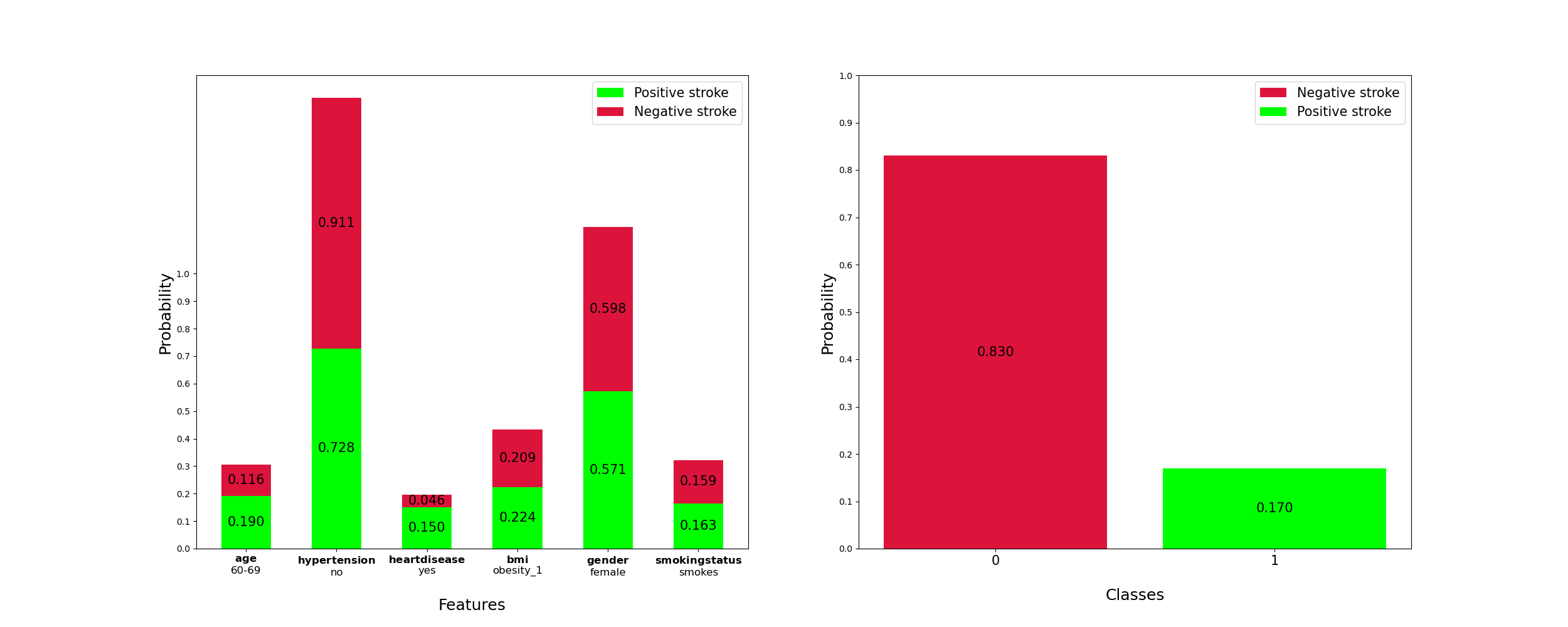
𝑎𝑔𝑒:60−69
ℎ𝑦𝑝𝑒𝑟𝑡𝑒𝑛𝑠𝑖𝑜𝑛:𝑛𝑜
ℎ𝑒𝑎𝑟𝑡_𝐷𝑖𝑠𝑒𝑎𝑠𝑒𝑦𝑒𝑠
𝑏𝑚𝑖:𝑜𝑏𝑒𝑠𝑖𝑡𝑦_1
𝑔𝑒𝑛𝑑𝑒𝑟:𝑓𝑒𝑚𝑎𝑙𝑒
𝑠𝑚𝑜𝑘𝑖𝑛𝑔𝑠𝑡𝑎𝑡𝑢𝑠:𝑠𝑚𝑜𝑘𝑒𝑠
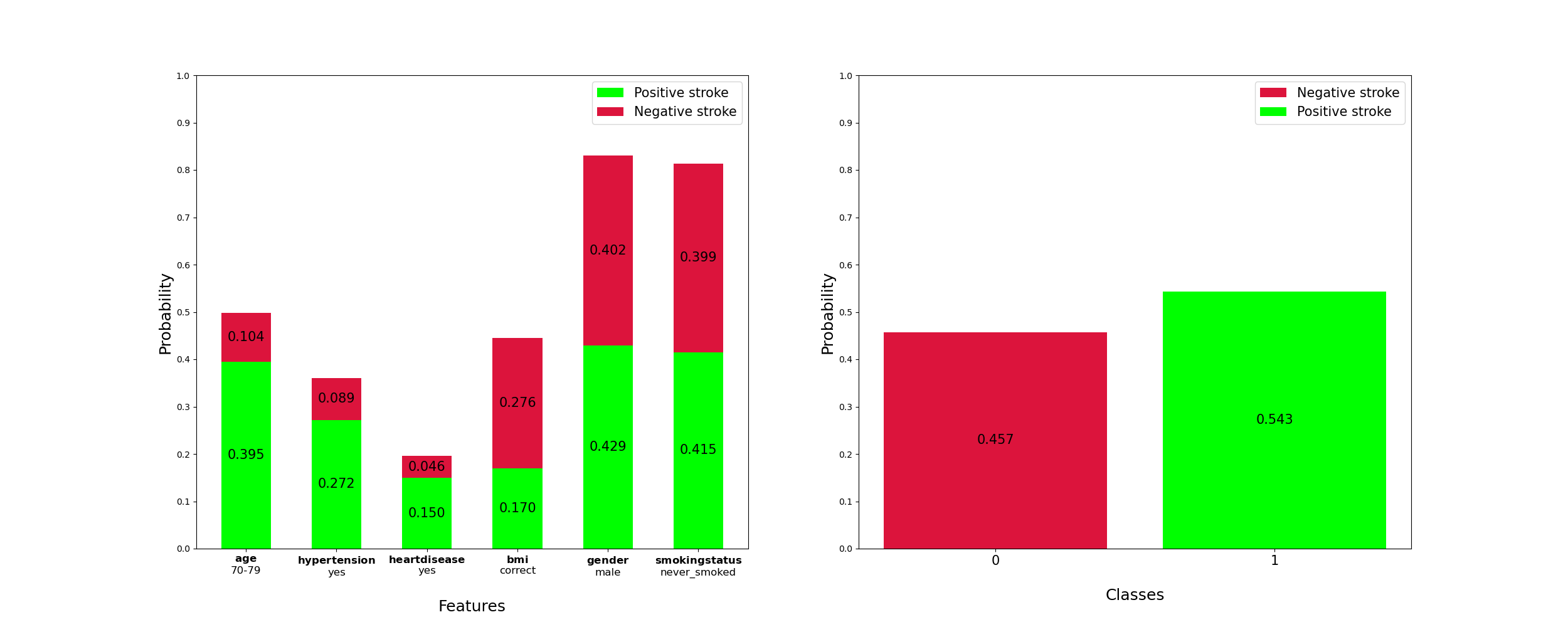
𝑎𝑔𝑒:70−79
ℎ𝑦𝑝𝑒𝑟𝑡𝑒𝑛𝑠𝑖𝑜𝑛: yes
ℎ𝑒𝑎𝑟𝑡_𝐷𝑖𝑠𝑒𝑎𝑠𝑒: 𝑦𝑒𝑠
𝑏𝑚𝑖:correct
𝑔𝑒𝑛𝑑𝑒𝑟:𝑚𝑎𝑙𝑒
𝑠𝑚𝑜𝑘𝑖𝑛𝑔𝑠𝑡𝑎𝑡𝑢𝑠:never_𝑠𝑚𝑜𝑘𝑒d
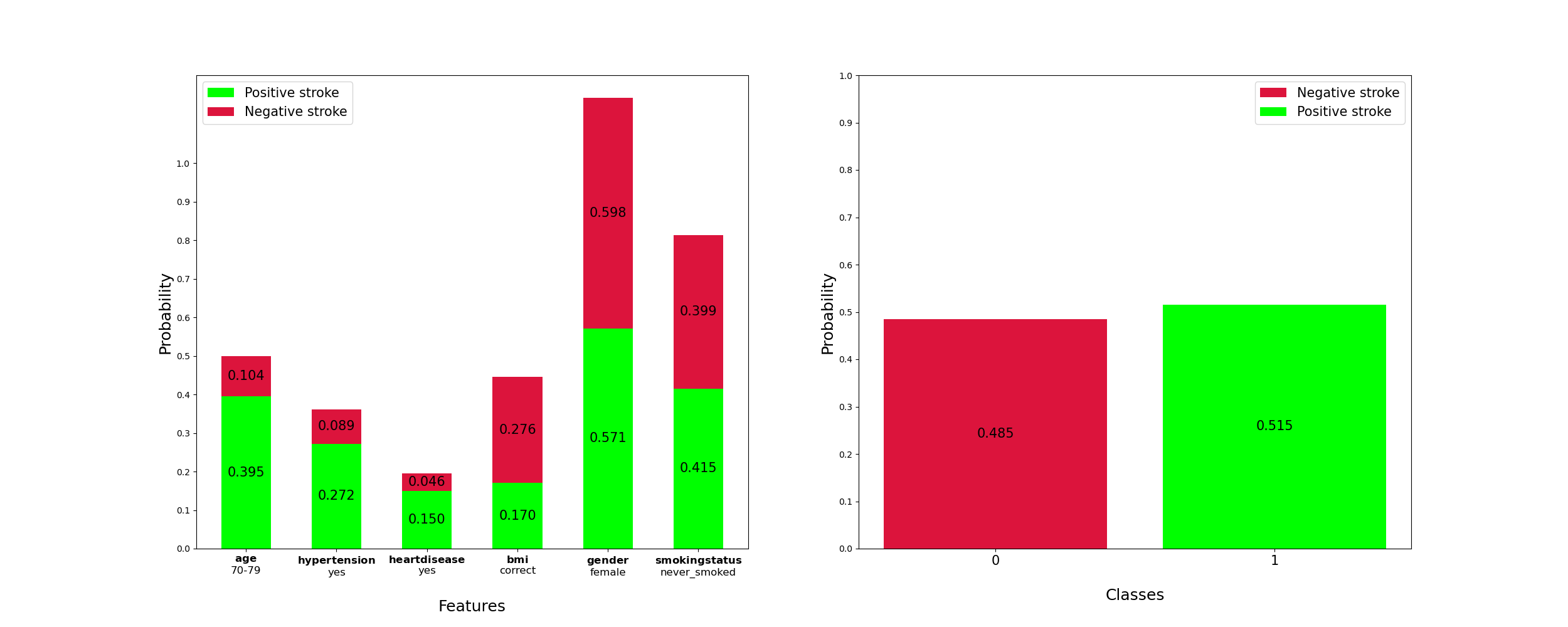
𝑎𝑔𝑒:70−79
ℎ𝑦𝑝𝑒𝑟𝑡𝑒𝑛𝑠𝑖𝑜𝑛: yes
ℎ𝑒𝑎𝑟𝑡_𝐷𝑖𝑠𝑒𝑎𝑠𝑒: 𝑦𝑒𝑠
𝑏𝑚𝑖:correct
𝑔𝑒𝑛𝑑𝑒𝑟:fe𝑚𝑎𝑙𝑒
𝑠𝑚𝑜𝑘𝑖𝑛𝑔𝑠𝑡𝑎𝑡𝑢𝑠:never_𝑠𝑚𝑜𝑘𝑒d
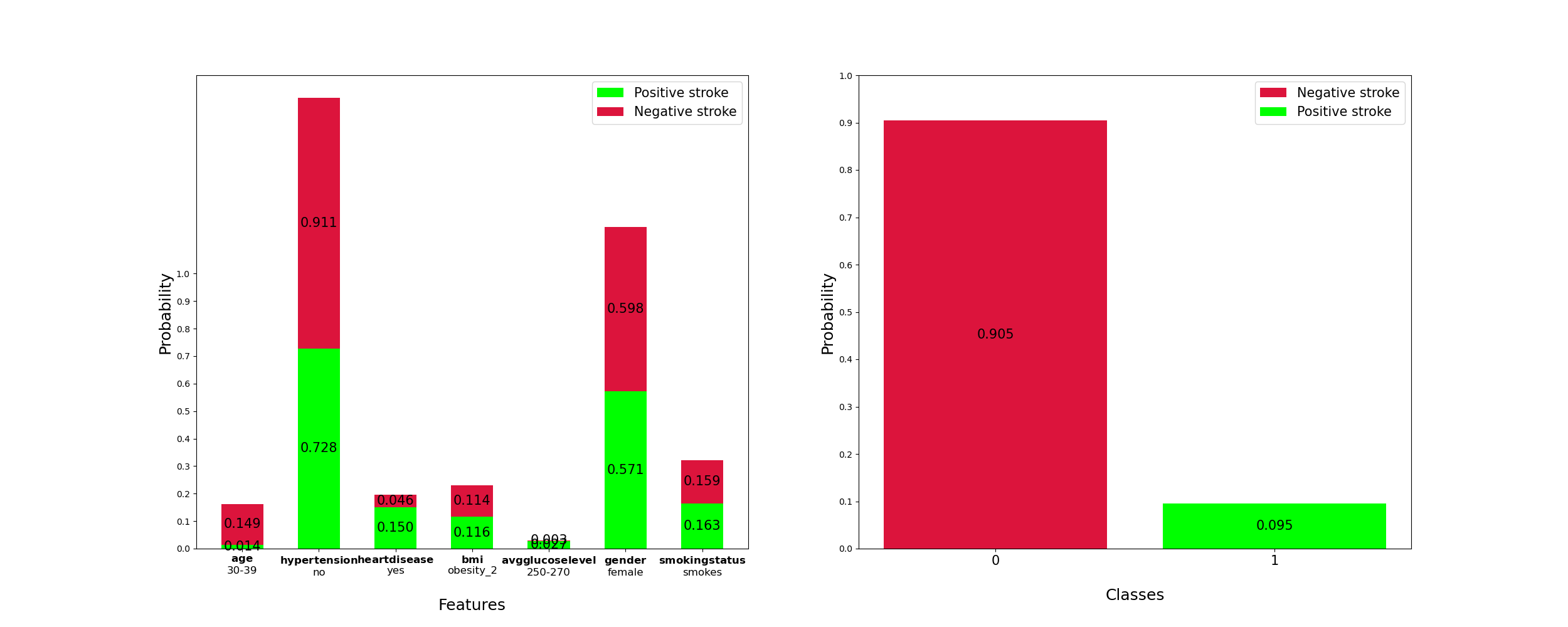
𝑎𝑔𝑒:30−39
ℎ𝑦𝑝𝑒𝑟𝑡𝑒𝑛𝑠𝑖𝑜𝑛: no
ℎ𝑒𝑎𝑟𝑡_𝐷𝑖𝑠𝑒𝑎𝑠𝑒: 𝑦𝑒𝑠
𝑏𝑚𝑖: obesity_2
avg_glucose_level: 250-270
𝑔𝑒𝑛𝑑𝑒𝑟:fe𝑚𝑎𝑙𝑒
𝑠𝑚𝑜𝑘𝑖𝑛𝑔𝑠𝑡𝑎𝑡𝑢𝑠:smokes
