7.6 KiB
Podprojekt: drzewa decyzyjne
Andrzej Preibisz
Opis problemu
Metodą uczenia, którą postanowiłem zaimplementować w projekcie były drzewa decyzyjne. Pola reprezentujące regały, lub chłodziarki różnią się między sobą temperaturą, oraz wilgotnością powietrza w danym miejscu. Paczki z kolei mogą zawierać towary następujących rodzajów:
- towar zwykły(normal)
- mrożony(freezed)
- kruchy(fragile)
- łatwo niszczejący pod wpływem wilgoci (keep_dry)
- łatwopalne(flammable)
Paczki zawierające określony rodzaj towarów mają pewne parametry środowiskowe, w których zdecydowanie nie powinno się danego typu towaru przechowywać. Jako przykład może posłużyć mrożone jedzenie, którego stan stosunkowo szybko ulegnie pogorszeniu w temperaturze dodatniej, lub lakier, który zdecydowanie nie powinien znaleźć się w części magazynu, gdzie panuje temperatura 30 stopni.
Celem drzewa decyzyjnego jest w tym wypadku przewidzenie prawdopodobnej szansy na to, że towar po przechowywaniu na danym regale przez dłuższy czas będzie w dobrym stanie.
Zastosowane drzewo
Drzewa decyzyjne dzielą się ogólnie na dwa rodzaje - drzew klasyfikujących, lub drzew regresyjnych. Drzewo klasyfikujące pozwala podzielić zmienna przewidywaną na kategorie, na przykład Tak i Nie.
Drzewo regresyjne z kolei dostarczy nam informacji o oczekiwanej wartości zmiennej estymowanej przy danej wartości atrybutów.
W świecie projektu różny rodzaj towarów ma różne "progi", od których można go kłaść na regale X, na przykład kładąc paczkę z lakierem/benzyną na regale lepiej mieć trochę większą pewność, że towar nie nagrzeje się nadmiernie, aniżeli kładąc książkę - że nie zniszczeje od wilgoci. W związku z tym zamiast prostej odpowiedzi Tak/Nie na pytanie czy dany obiekt można położyć na danym regale potrzebna była przewidywana wartość prawdopodobieństwa że w danym miejscu zachowa się on w dobrym stanie. Wszystkie te progi wynoszą odpowiednio:
PACKAGE_PLACE_TRESHOLD = {
"normal": 0.8,
"freezed": 0.85,
"fragile": 0.85,
"flammable": 0.9,
"keep_dry": 0.8
}
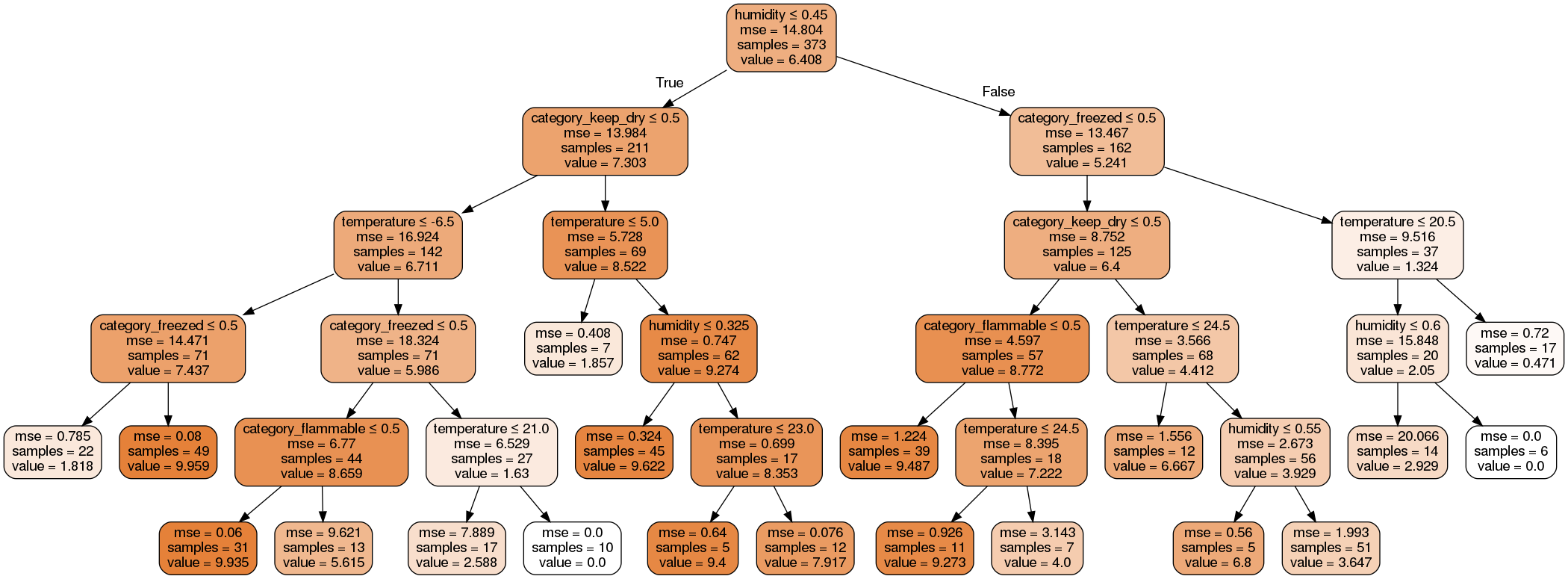
Zdecydowałem się więc na wybór drzewa regresyjnego. Biblioteką której użyłem w celu implementacji drzewa jest scikit-learn. Najważniejszym problemem oprócz dokładności oszacowań dokonanych przy pomocy drzewa było uniknięcie overfittingu(przepasowania), czyli sytuacji, w której drzewo perfekcyjnie dopasuje się do danych ze zbioru uczącego, jednak z danymi spoza tego zbioru poradzi sobie już dużo gorzej. Oprócz błędnej oceny danych innych niż ze zbioru uczącego sygnałem wskazującym na overfitting drzewa jest zbyt duża jego głębokość drzewa (odległość od korzenia do najdalszego liścia), oraz liście zawierające tylko 1 rekord. W celu uniknięcia overfittingu zdecydowałem się na ograniczenie maksymalnej głębokości drzewa, oraz na ustawienie minimalnej ilości rekordów w liściu. Drzewo wraz z odpowiednimi ograniczeniami zdefiniowane jest w następujący sposób
clf = DecisionTreeRegressor(ccp_alpha=0.02, min_samples_leaf=5, max_depth=5)
gdzie argumenty min_samples_leaf, oraz max_depth oznaczają odpowiednio minimalną ilość rekordów(przykładów ze zbioru uczącego) w liściu, oraz maksymalną głębokość drzewa.
Argument ccp_alpha oznacza parametr \alpha stosowany przy complexity-cost pruning. Pruning oznacza dalsze przycięcie drzewa, aby uniknąć overfittingu
Kryterium według którego mierzona jest "jakość" rozgałęzienia jest tzw. MSE(Mean Squared Error), czyli błąd średniokwadratowy(średnia kwadratów odchylenia wielkości oczekiwanej od rzeczywistej).
Dobierając te parametry wyszedłem z założenia że jeżeli 5 rekordów będzie w jednym liściu, to znaczy że najprawdopodbniej zachodzi
już w ich przypadku pewna prawidłowość, i mają one jakieś wspólne cechy, które determinują taką, a nie inną wartość przewidywaną,
w odróżnieniu od sytuacji gdy liść zawierałby tylko 1-2 rekordy, co wskazywałoby na bardzo specyficzne parametry takiego/ich rekordu/ów,
i prawdopodobnie oznaczało overfitting drzewa. W przypadku głębokości chodziło o uniknięcie nadmiernego rozrostu drzewa.
Zastosowany zbiór uczący obejmuje 373 rekordy zapisane w formacie .csv, w którym poszczególne kolumny oznaczają odpowiednio:
produkt, kategorię produktu, temperature na regale, wilgotność powietrza na danym regale, szansę że przedmiot po dłuższym czasie przechowywania będzie w dobrym stanie, oraz informację czy można bezpiecznie go tu położyć.
Przykładowy rekord: frozen food,freezed,21, 0.5, 0.01, 0 . Zbiór testowy z kolei zawiera 26 rekordów w tym samym formacie.
Zbiór uczący znajduje się w pliku package_location_classifier/trainset/trainset.csv, a testowy package_location/testset/testset.csv.
Przygotowanie zbioru uczącego i testowego dla drzewa:
products = pd.read_csv("package_location_classifier/trainset/trainset.csv", header=0, sep=",", names=cols_names)
testset = pd.read_csv("package_location_classifier/testset/testset.csv", header=None, sep=",", names=cols_names)
products = products.round({"chance_of_survive": 1})
testset = testset.round({"chance_of_survive": 1})
products.chance_of_survive *= 10
testset.chance_of_survive *= 10
test_X = pd.get_dummies(testset[feature_cols])
test_y = testset.chance_of_survive
products = products.sample(frac=1)
X_train = pd.get_dummies(products[feature_cols])
y_train = products.chance_of_survive
Uczenie drzewa i ewaluacja przy pomocy zbioru testowego:
self.predictor = clf.fit(X_train, y_train)
y_pred = self.predictor.predict(test_X)
Graficzna reprezentacja drzewa wygenerowanego dla tego zbioru uczącego:
Wyniki ewaluacji zestawu testowego, znajdujące się w pliku Test_results.xlsx:
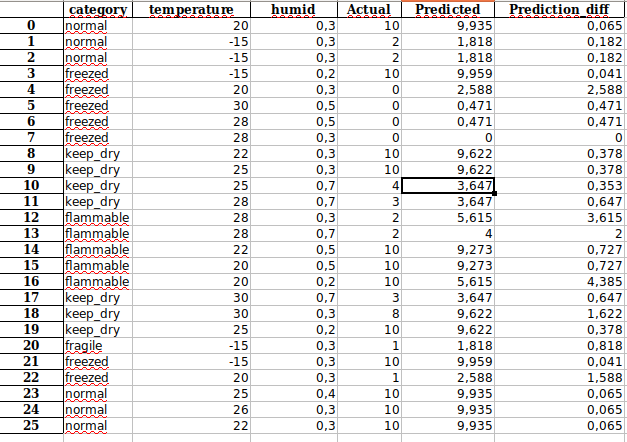
Przewidywana wartość w zestawie testowym różni się od wartości faktycznej średnio o 0.87, jako że w raporcie wartości są pomnożone przez 10, daje to średnio 0.087 wartości różnicy w czasie działania drzewa.
Zastosowanie drzewa w części wspólnej projektu
Po podniesieniu paczki przez agenta odpalana jest funkcja szukająca najbliższego pasującego regału. Przy poszukiwaniu takiego regału stosowana jest funkcja heurystyczna o następującym kodzie:
def rack_heuristics(self, start, goal, can_place):
heur_can_place = not can_place
diff_x = pow(goal.x - start.x, 2)
diff_y = pow(goal.y - start.y, 2)
place_cost = 100 * float(heur_can_place)
return round(sqrt(diff_x + diff_y), 3) + float(place_cost)
Parametr can_place to wynik ewaluacji pola goal, przy pomocy drzewa:
for rack in quarter_racks:
new_node = Node(rack.x_position, rack.y_position)
can_place = self.location_classifier.check_if_can_place(package, rack)
cost = self.rack_heuristics(start_node, new_node, can_place)
self.location_classifier, to obiekt klasy PackageLocationClassifier. Klasa ta zawiera metodę check_if_can_place() :
def check_if_can_place(self, package, tile):
category = package.category
cat_treshold = PACKAGE_PLACE_TRESHOLD[category]
fields = [[
tile.air_temperature,
tile.humidity,
category == "flammable",
category == "fragile",
category=="freezed" ,
category == "keep_dry",
category == "normal"
]]
quality_of_place = round(self.predictor.predict(fields)[0]/10, 2)
if quality_of_place > cat_treshold:
return True
return False
Self.predictor to nauczone drzewo.