aitech-eks-pub/wyk/09_neurozoo.ipynb

Neurozoo

Kilka uwag dotyczących wektorów

Wektor wierszowy $\left[x_1,\dots,x_n\right]$ czy kolumnowy $\left[\begin{array}{c} x_1 \\ \vdots \\ x_n\end{array}\right]$?

Często zakłada się wektor kolumny, będziemy używać transpozycji, by otrzymać wektor wierszowy $\vec{x}^T = \left[x_1,\dots,x_n\right]$.

W praktyce, np. w PyTorchu, może to nie mieć wielkiego znaczenia:

import torch
x = torch.tensor([1.0, -0.5, 2.0])
x

# Out[2]:
tensor([ 1.0000, -0.5000,  2.0000])

Musimy tylko uważać, jeśli przemnażamy wektor przez macierz!

Funkcja sigmoidalna

Funkcja sigmoidalna zamienia dowolną wartość („sygnał”) w wartość z przedziału $(0,1)$, czyli wartość, która może być interperetowana jako prawdopodobieństwo.

$$\sigma(x) = \frac{1}{1 + e^{-x}}$$

import torch

def sigmoid(x):
    return 1 / (1 + torch.exp(-x))

sigmoid(torch.tensor(0.6))

# Out[1]:
tensor(0.6457)

%matplotlib inline
import matplotlib.pyplot as plt
import torch

x = torch.linspace(-5,5,100)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, sigmoid(x))
fname = 'sigmoid.png'
plt.savefig(fname)
fname

[[file:# Out[32]:

'sigmoid.png'

]]

PyTorch

Funkcja torch.sigmoid po prostu stosuje sigmoidę do każdego elementu tensora (_element-wise).

import torch

torch.sigmoid(torch.tensor([0.6, 1.0, -5.0]))

# Out[38]:
tensor([0.6457, 0.7311, 0.0067])

Istnieje również torch.nn.Sigmoid, które może być używane jako warstwa.

import torch.nn as nn

s = nn.Sigmoid()
s(torch.tensor([0.0, -0.2, 0.4]))

# Out[49]:
tensor([0.5000, 0.4502, 0.5987])

Implementacja w Pytorchu

import torch.nn as nn
import torch

class MySigmoid(nn.Module):
    def __init__(self):
        super(MySigmoid, self).__init__()

    def forward(self, x):
        return 1 / (1 + torch.exp(-x))

s = MySigmoid()
s(torch.tensor([0.0, 0.5, 0.3]))

# Out[48]:
tensor([0.5000, 0.6225, 0.5744])

Wagi

Funkcja sigmoidalna nie ma żadnych wyuczalnych wag.

Pytanie: Czy można rozszerzyć funkcję sigmoidalną o jakieś wyuczalne wagi?

Regresja liniowa

Iloczyn skalarny — przypomnienie

$$\left[1.0, -0.5, 2.0\right] \left[\begin{array}{c} 3.0 \\ 1.5 \\ 0.0\end{array}\right] = 1.0 \cdot 3.0 + -0.5 \cdot 1.5 + 2.0 \cdot 0.0 = 2.25$$

Intuicje

• $\vec{a}^T \vec{b}$ mierzy jak bardzo $\vec{a}$ „pasuje” do $\vec{b}$,
• … zwłaszcza gdy znormalizujemy wektory dzieląc przez $|\vec{a}|$ i $|\vec{b}|$: $\frac{\vec{a}^T \vec{b}}{|\vec{a}||\vec{b}|} = \cos \theta$, gdzie $\theta$ to kąt pomiędzy $\vec{a}$ and $\vec{b}$ (podobieństwo kosinusowe!)
• co, jeśli if $\vec{a}^T \vec{b} = 0$? — $\vec{a}$ i $\vec{b}$ są prostopadłe, np. $\left[1, 2\right] \cdot \left[-2, -1\right]^T = 0$
• a co, jeśli $\vec{a}^T \vec{b} = -1$ — wektor są skierowane w przeciwnym kierunku, jeśli dodatkowo $|\vec{a}|=|\vec{b}|=1$, np. $\left[\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right] \cdot \left[-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right]^T = -1$

W PyTorchu

import torch
x = torch.tensor([1.0, -0.5, 2.0])
y = torch.tensor([3.0, 1.5, 0.0])
x @ y

# Out[3]:
tensor(2.2500)

Regresja liniowa jako element sieci neuronowej

Przypomnijmy sobie wzór na regresję liniową:

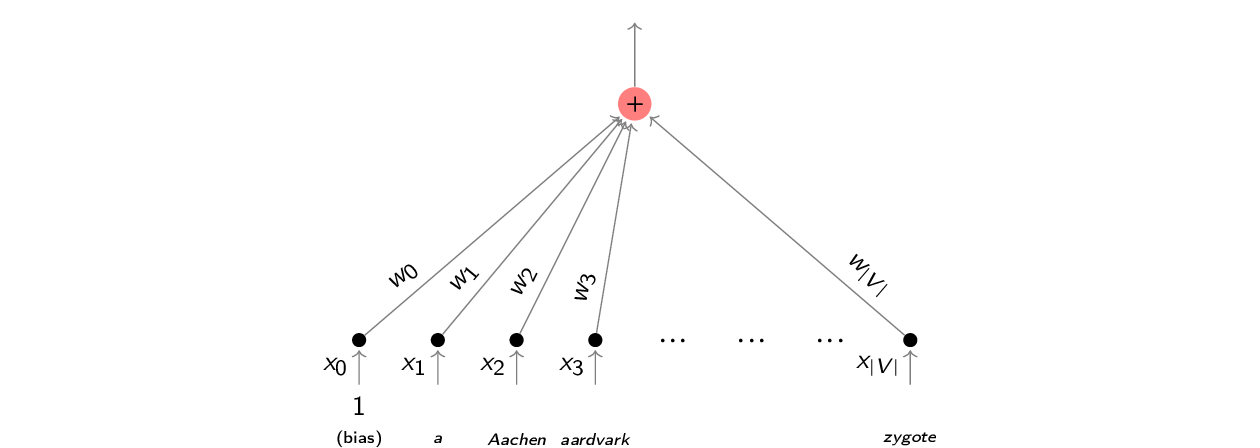
$$y = w_0 + w_1x_1 + w_2x_2 + \dots + w_{|V|}x_{|v|}$$

Jeśli wprowadzimy sztuczny element wektora $\vec{x}$ ustawiony zawsze na 1 ($x_0 = 1$), wówczas wzór może przyjąc bardziej zwartą postać:

$$y = \sum_{i=0}^{|V|} w_ix_i = \vec{w}\vec{x}$$

PyTorch

Implementacja w PyTorchu

Zakładamy, że wektor wejściowy nie obejmuje dodatkowego elementu $x_0 = 1$.

import torch
import torch.nn as nn

class MyLinearRegressor(nn.Module):
     def __init__(self, vlen):
         super(MyLinearRegressor, self).__init__()
         self.register_parameter(name='w', param=torch.nn.Parameter(
             torch.zeros(vlen, dtype=torch.double, requires_grad=True)))
         self.register_parameter(name='b', param=torch.nn.Parameter(
             torch.tensor(0., dtype=torch.double, requires_grad=True)))

     def forward(self, x):
         return self.b + x @ self.w

regressor = MyLinearRegressor(3)
regressor(torch.tensor([0.3, 0.4, 1.0], dtype=torch.double))

# Out[11]:
tensor(0., dtype=torch.float64, grad_fn=<AddBackward0>)

Gotowy moduł w PyTorchu

Możemy skorzystać z ogólniejszej konstrukcji — warstwy liniowej (ale, uwaga!, na wyjściu będzie wektor jednoelementowy).

import torch
import torch.nn as nn

regressor = torch.nn.Linear(in_features=3, out_features=1, bias=True)
regressor(torch.tensor([0.3, 0.4, 1.0]))

# Out[18]:
tensor([0.1882], grad_fn=<AddBackward0>)

Zastosowania

Bezpośrednio możemy zastosować do zadania regresji dla tekstu (np. przewidywanie roku publikacji tekstu).

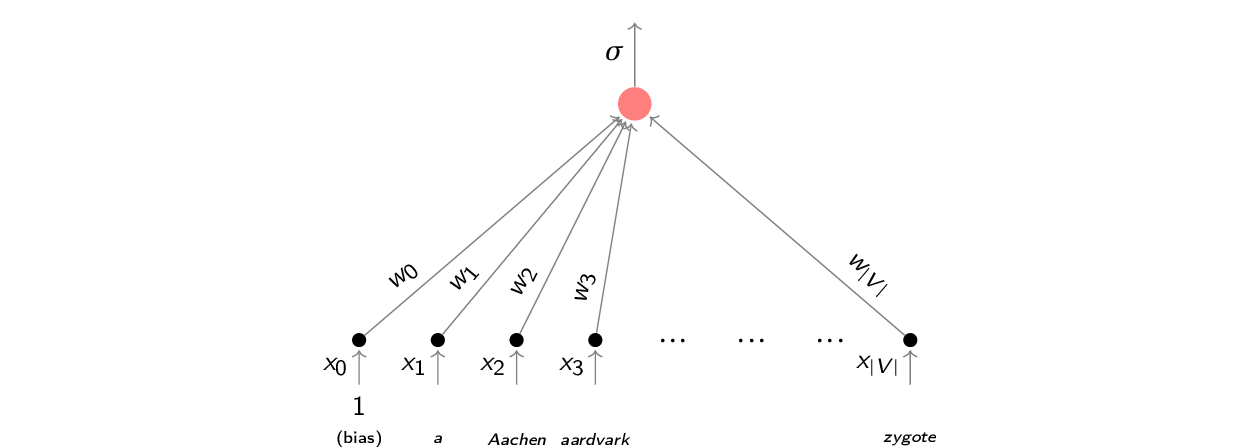
W połączeniu z sigmoidą otrzymamy regresją logistyczną, np. dla zadania klasyfikacji tekstu:

$$p(c|\vec{x}) = \sigma(w_0 + w_1x_1 + w_2x_2 + \dots + w_{|V|}x_{|v}) = \sigma(\Sigma_{i=0}^{|V|} w_ix_i) = \sigma(\vec{w}\vec{x})$$

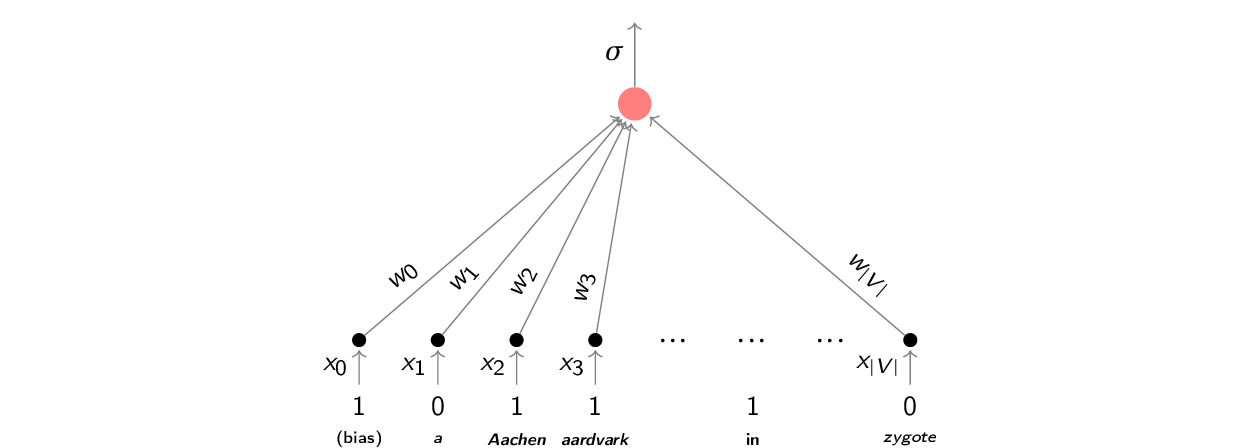
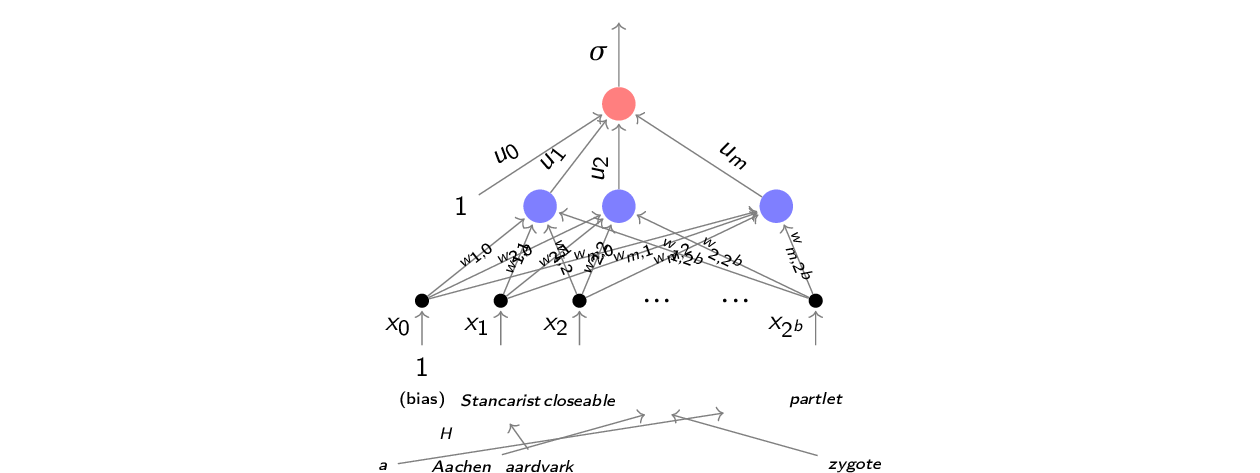
Tak sieć będzie aktywowana dla tekstu aardvark in Aachen:

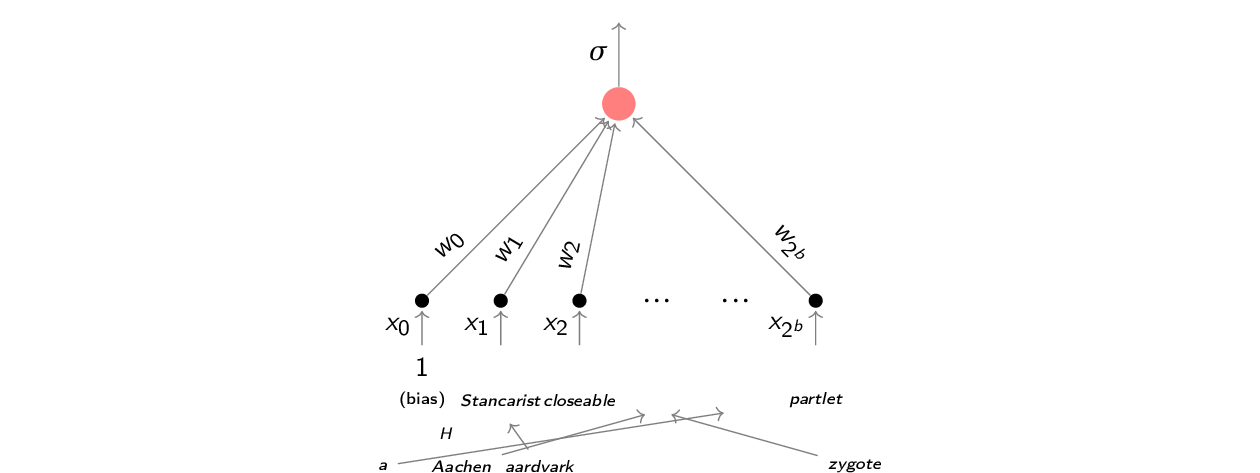
Regresje logistyczną (liniową zresztą też) dla tekstu możemy połączyć z trikiem z haszowaniem:

$$p(c|\vec{x}) = \sigma(w_0 + w_1x_1 + w_2x_2 + \dots + w_{2^b}x_{2^b}) = \sigma(\Sigma_{i=0}^{2^b} w_ix_i) = \sigma(\vec{w}\vec{x})$$
{\small hashing function $H : V \rightarrow \{1,\dots,2^b\}$, e.g. MurmurHash3}

Pytanie: Jaki tekst otrzyma na pewno taką samą klasę jak aardvark in Aachen?

Wagi

Liczba wag jest równa rozmiarowi wektora wejściowego (oraz opcjonalnie obciążenie).

Każda waga odpowiada wyrazowi ze słownika, możemy więc interpretować wagi jako jednowymiarowy parametr opisujący słowa.

Warstwa liniowa

Mnożenie macierzy przez wektor — przypomnienie

Mnożenie macierzy przez wektor można interpretować jako zrównolegloną operację mnożenie wektora przez wektor.

$$\left[\begin{array}{ccc} \alert<2>{1.0} & \alert<2>{-2.0} & \alert<2>{3.0} \\ \alert<3>{-2.0} & \alert<3>{0.0} & \alert<3>{10.0}\end{array}\right] \left[\begin{array}{c} \alert<2-3>{1.0} \\ \alert<2-3>{-0.5} \\ \alert<2-3>{2.0}\end{array}\right] = \left[\begin{array}{c} \uncover<2->{\alert<2>{8.0}} \\ \uncover<3->{\alert<3>{18.0}}\end{array}\right]$$

Jeśli przemnożymy macierz $n \times m$ przez wektor kolumnowy o długości $m$, otrzymamy wektor o rozmiarze $n$.

W PyTorchu:

import torch
m = torch.tensor([[1.0, -2.0, 3.0],
                  [-2.0, 0.0, 10.0]])
x = torch.tensor([1.0, -0.5, 2.0])
m @ x

[[file:# Out[19]:

tensor([ 8., 18.])]]

Definicja warstwy liniowej

Warstwa liniowa polega na przemnożeniu wejścia przez macierz. Można to intepretować jako zrównolegloną operację regresji liniowej (równolegle uczymy czy wykonujemy $n$ regresji liniowych).

PyTorch

Warstwa liniowa, która przyjmuje wektor o rozmiarze 3 i zwraca wektor o rozmiarze 2.

import torch
import torch.nn as nn

regressor = torch.nn.Linear(in_features=3, out_features=2, bias=True)
regressor(torch.tensor([0.3, 0.4, 1.0]))

# Out[23]:
tensor([-1.1909, -0.5831], grad_fn=<AddBackward0>)

Pytanie: Ile wag (parametrów) ma powyżej użyta warstwa?

Zastosowania

Warstwa liniowa jest podstawowym elementem sieci neuronowych — począwszy od prostych sieci neuronowych feed-forward, gdzie warstwy liniowe łączymy używając funkcji aktywacji (np. sigmoidy).

Oto przykład prostej dwuwarstwowej sieci neuronowej do klasyfikacji binarnej.

Softmax

W klasyfikacji wieloklasowej należy zwrócić musimy zwrócić rozkład prawdopodobieństwa po wszystkich klasach, w przeciwieństwie do klasyfikacji binarnej, gdzie wystarczy zwrócić jedną liczbę — prawdopodobieństwo pozytywnej klasy ($p$; prawdopodobieństwo drugiej klasy to po prostu $1-p$).

A zatem na potrzeby klasyfikacji wieloklasowej potrzeba wektorowego odpowiednika funkcji sigmoidalnej, to jest funkcji, która zamienia nieznormalizowany wektor $\vec{z} = [z_1,\dots,z_k]$ (pochodzący np. z poprzedzającej warstwy liniowej) na rozkład prawdopobieństwa. Potrzebujemy zatem funkcji $s: \mathcal{R}^k \rightarrow [0,1]^k$

spełniającej następujące warunki:

• $s(z_i) = s_i(z) \in [0,1]$
• $\Sigma_i s(z_i) = 1$
• $z_i > z_j \Rightarrow s(z_i) > s(z_j)$

Można by podać takie (błędne!) rozwiązanie:

$$s(z_i) = \frac{z_i}{\Sigma_{j=1}^k z_j}$$

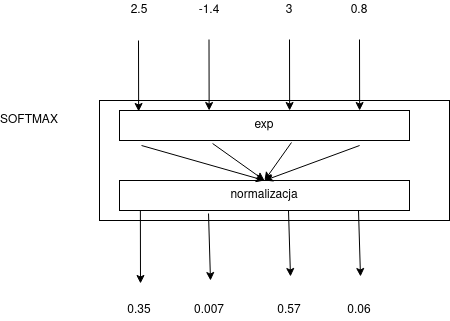
To rozwiązanie zadziała błędnie dla liczb ujemnych, trzeba najpierw użyć funkcji monotonicznej, która przekształaca $\mathcal{R}$ na $\mathcal{R^+}$. Naturalna funkcja tego rodzaju to funkcja wykładnicza $\exp{x} = e^x$. Tym sposobem dochodzimy do funkcji softmax:

$$s(z_i) = \frac{e^{z_i}}{\Sigma_{j=1}^k e^{z_j}}$$

Mianownik ułamka w definicji funkcji softmax nazywamy czasami czynnikiem normalizacyjnym: $Z(\vec{z}) = \Sigma_{j=1}^k e^{z_j}$, wtedy:

$$s(z_i) = \frac{e^{z_i}}{Z(\vec{z})}$$

Definicja w PyTorchu:

import torch

def softmax(z):
    z_plus = torch.exp(z)
    return z_plus / torch.sum(z_plus)

softmax(torch.tensor([3., -1., 0., 5.]))

# Out[75]:
tensor([0.1182, 0.0022, 0.0059, 0.8737])

Soft vs hard

Dlaczego _softmax? Czasami używa się funkcji hardmax, która np. wektora $[3, -1, 0, 5]$ zwróciłaby $[0, 0, 0, 5]$ — to jest po prostu wektorowa wersja funkcji zwracającej maksimum. Istnieje też funkcja hard*arg*max, która zwraca wektor _one-hot — z jedną jedynką na pozycji dla największej wartości (zamiast podania największej wartości), np. wartość hardargmax dla $[3, -1, 0, 5]$ zwróciłaby $[0, 0, 0, 1]$.

Zauważmy, że powszechnie przyjęta nazwa _softmax jest właściwie błędna, funkcja ta powinna nazywać się _softargmax, jako że w „miękki” sposób identyfikuje największą wartość przez wartość zbliżoną do 1 (na pozostałych pozycjach wektora nie będzie 0).

Pytanie: Jak można zdefiniować funkcję _softmax w ścisłym tego słowa znaczeniu („miękki” odpowiednik hardmax, nie hardargmax)?

PyTorch

Funkcja torch.nn.functional.softmax normalizuje wartości dla całego tensora:

import torch.nn as nn

nn.functional.softmax(torch.tensor([0.6, 1.0, -5.0]))

# Out[5]:
tensor([0.4007, 0.5978, 0.0015])

… zobaczmy, jak ta funkcja zachowuje się dla macierzy:

import torch.nn as nn

nn.functional.softmax(torch.tensor([[0.6, 1.0], [-2.0, 3.5]]))

# Out[6]:
#+BEGIN_EXAMPLE
  tensor([[0.4013, 0.5987],
  [0.0041, 0.9959]])
#+END_EXAMPLE

Za pomocą (zalecanego zresztą) argumentu dim możemy określić wymiar, wzdłuż którego dokonujemy normalizacji:

import torch.nn as nn

nn.functional.softmax(torch.tensor([[0.6, 1.0], [-2.0, 3.5]]), dim=0)

# Out[8]:
#+BEGIN_EXAMPLE
  tensor([[0.9309, 0.0759],
  [0.0691, 0.9241]])
#+END_EXAMPLE

Istnieje również torch.nn.Softmax, które może być używane jako warstwa.

import torch.nn as nn

s = nn.Softmax(dim=0)
s(torch.tensor([0.0, -0.2, 0.4]))

# Out[10]:
tensor([0.3021, 0.2473, 0.4506])

Implementacja w Pytorchu

import torch.nn as nn
import torch

class MySoftmax(nn.Module):
    def __init__(self):
        super(MySoftmax, self).__init__()

    def forward(self, x):
        ex = torch.exp(x)
        return ex / torch.sum(ex)

s = MySigmoid()
s(torch.tensor([0.0, 0.5, 0.3]))

# Out[48]:
tensor([0.5000, 0.6225, 0.5744])

Pytanie: Tak naprawdę wyżej zdefiniowana klasa MySoftmax nie zachowuje się identycznie jak nn.Softmax. Na czym polega różnica?

Przypadek szczególny

Sigmoida jest przypadkiem szczególnym funkcji softmax:

$$\sigma(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{e^x + 1} = \frac{e^x}{e^x + e^0} = s([x, 0])_1$$

Ogólniej: softmax na dwuelementowych wektorach daje przesuniętą sigmoidę (przy ustaleniu jednej z wartości).

%matplotlib inline
import matplotlib.pyplot as plt
import torch
import torch.nn as nn

x = torch.linspace(-5,5,100)
plt.xlabel("x")
plt.ylabel("y")
a = torch.Tensor(x.size()[0]).fill_(2.)
m = torch.stack([x, a])
plt.plot(x, nn.functional.softmax(m, dim=0)[0])
fname = 'softmax3.png'
plt.savefig(fname)
fname

[[file:# Out[19]:

'softmax3.png'

]]

%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
import torch
import torch.nn as nn

x = torch.linspace(-5,5,10)
y = torch.linspace(-5,5,10)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
plt.xlabel("x")
plt.ylabel("y")
X, Y = torch.meshgrid(x, y)
m = torch.stack([X, Y])
z = nn.functional.softmax(m, dim=0)
ax.plot_wireframe(x, y, z[0])
fname = 'softmax3d.png'
plt.savefig(fname)
fname

[[file:# Out[27]:

'softmax3d.png'

]]

Wagi

Podobnie jak funkcja sigmoidalna, softmax nie ma żadnych wyuczalnych wag.

Zastosowania

Podstawowym zastosowaniem funkcji softmax jest klasyfikacja wieloklasowa, również w wypadku zadań przetwarzania sekwencji, które mogą być interpretowane jako klasyfikacja wieloklasowa:

• przewidywanie kolejnego słowa w modelowaniu języka (klasą jest słowo, zbiór klas to słownik, np. klasą początku tekstu _Dzisiaj rano kupiłem w piekarni może być bułki)
• przypisywanie etykiet (np. części mowy) słowom.

LogSoftmax

Ze względów obliczeniowych często korzysta się z funkcji LogSoftmax która zwraca logarytmy pradopodobieństw (_logproby).

$$log s(z_i) = log \frac{e^{z_i}}{\Sigma_{j=1}^k e^{z_j}}$$

PyTorch

import torch.nn as nn

s = nn.LogSoftmax(dim=0)
s(torch.tensor([0.0, -0.2, 0.4]))

# Out[25]:
tensor([-1.1971, -1.3971, -0.7971])

Niektóre funkcje kosztu (np. NLLLoss) zaimplementowane w PyTorchu operują właśnie na logarytmach prawdopobieństw.

Przykład: klasyfikacja wieloklasowa

Na przykładzie rozpoznawania dyscypliny sportu: git://gonito.net/sport-text-classification.git

Wczytujemy zbiór uczący:

import gzip
from pytorch_regression.analyzer import vectorize_text, vector_length

texts = []
labels = []
labels_dic = {}
labels_revdic = {}
c = 0

with gzip.open('sport-text-classification/train/train.tsv.gz', 'rt') as fh:
  for line in fh:
    line = line.rstrip('\n')
    line = line.replace('\\\\\t', ' ')
    label, text = line.split('\t')
    texts.append(text)
    if label not in labels_dic:
       labels_dic[label] =c
       labels_revdic[c] = label
       c += 1
    labels.append(labels_dic[label])
nb_of_labels = len(labels_dic)
labels_dic

# Out[85]:
#+BEGIN_EXAMPLE
  {'zimowe': 0,
  'moto': 1,
  'tenis': 2,
  'pilka-reczna': 3,
  'sporty-walki': 4,
  'koszykowka': 5,
  'siatkowka': 6,
  'pilka-nozna': 7}
#+END_EXAMPLE

Przygotowujemy model:

import torch.nn as nn
from torch import optim

model = nn.Sequential(
        nn.Linear(vector_length, nb_of_labels),
        nn.LogSoftmax()
      )

optimizer = optim.Adam(model.parameters())

# Out[8]:

Funkcja kosztu to log-loss.

import torch
import torch.nn.functional as F

loss_fn = torch.nn.NLLLoss()

expected_class_id = torch.tensor([2])
loss_fn(torch.log(
           torch.tensor([[0.3, 0.5, 0.1, 0.0, 0.1]])),
        expected_class_id)

# Out[9]:
tensor(2.3026)

Pętla ucząca:

iteration = 0
step = 50
closs = torch.tensor(0.0, dtype=torch.float, requires_grad=False)

for t, y_exp in zip(texts, labels):
  x = vectorize_text(t).float().unsqueeze(dim=0)

  optimizer.zero_grad()

  y_logprobs = model(x)

  loss = loss_fn(y_logprobs, torch.tensor([y_exp]))

  loss.backward()

  with torch.no_grad():
      closs += loss

  optimizer.step()

  if iteration % 50 == 0:
     print((closs / step).item(), loss.item(), iteration, y_exp, torch.exp(y_logprobs), t)
     closs = torch.tensor(0.0, dtype=torch.float, requires_grad=False)
  iteration += 1

  if iteration == 5000:
     break

# Out[86]:

Model jest tak prosty, że jego wagi są interpretowalne.

with torch.no_grad():
  x = vectorize_text('NBA').float().unsqueeze(dim=0)
  y_prob = model(x)
torch.exp(y_prob)

# Out[26]:
tensor([[0.0070, 0.0075, 0.0059, 0.0061, 0.0093, 0.9509, 0.0062, 0.0071]])

with torch.no_grad():
  x = vectorize_text('NBA').float().unsqueeze(dim=0)
  ix = torch.argmax(x).item()
model[0].weight[:,ix]

# Out[89]:
#+BEGIN_EXAMPLE
  Parameter containing:
  tensor([[ 7.8818e-04,  1.0930e-03,  5.9632e-04,  ...,  8.1697e-04,
  1.2976e-03, -8.4243e-04],
  [-1.0164e-03, -8.9416e-04, -1.8650e-03,  ...,  6.6075e-04,
  -5.4883e-04, -1.1845e-03],
  [-3.1395e-04,  1.8564e-03, -7.0267e-04,  ..., -4.7028e-04,
  7.0584e-04,  9.8026e-04],
  ...,
  [ 4.8792e-05,  1.9183e-03,  1.3152e-03,  ...,  4.6495e-04,
  9.5338e-04,  1.9107e-03],
  [-5.2181e-04,  1.1135e-03,  7.1943e-04,  ...,  3.7215e-04,
  1.0002e-03, -1.7985e-03],
  [-9.1641e-04,  1.6301e-03,  1.7372e-03,  ...,  1.2390e-03,
  -9.1001e-04,  1.5711e-03]], requires_grad=True)
#+END_EXAMPLE

Możemy nawet zaprezentować wykres przedstawiający rozmieszczenie słów względem dwóch osi odnoszących się do poszczególnych wybranych dyscyplin.

%matplotlib inline
import matplotlib.pyplot as plt

with torch.no_grad():
    words = ['piłka', 'klub', 'kort', 'boisko', 'samochód']
    words_ixs = [torch.argmax(vectorize_text(w).float().unsqueeze(dim=0)).item() for w in words]

    x_label = labels_dic['pilka-nozna']
    y_label = labels_dic['tenis']

    x = [model[0].weight[x_label, ix] for ix in words_ixs]
    y = [model[0].weight[y_label, ix] for ix in words_ixs]

    fig, ax = plt.subplots()
    ax.scatter(x, y)

    for i, txt in enumerate(words):
        ax.annotate(txt, (x[i], y[i]))

# Out[45]:

Zadanie etykietowania sekwencji

Zadanie etykietowania sekwencji (_sequence labelling) polega na przypisaniu poszczególnym wyrazom (tokenom) tekstu etykiet ze skończonego zbioru. Definiując formalnie:

• rozpatrujemy ciąg wejściowy tokenów $(t^1,\dots,t^K)$
• dany jest skończony zbiór etykiet $L = \{l_1,\dots,l_{|L|}\}$, dla uproszczenia można założyć, że etykietami są po prostu kolejne liczby, tj. $L=\{0,\dots,|L|-1\}$
• zadanie polega na wygenerowaniu sekwencji etykiet (o tej samej długości co ciąg wejściowy!) $(y^1,\dots,y^K)$, $y^k \in L$

Zadanie etykietowania można traktować jako przypadek szczególny klasyfikacji wieloklasowej, z tym, że klasyfikacji dokonujemy wielokrotnie — dla każdego tokenu (nie dla każdego tekstu).

Przykłady zastosowań:

• oznaczanie częściami mowy (_POS tagger) — czasownik, przymiotnik, rzeczownik itd.
• oznaczanie etykiet nazw w zadaniu NER (nazwisko, kwoty, adresy — najwięcej tokenów będzie miało etykietę pustą, zazwyczaj oznaczaną przez O)

Pytanie: czy zadanie tłumaczenia maszynowego można potraktować jako problem etykietowania sekwencji?

Przykładowe wyzwanie NER CoNLL-2003

Zob. https://gonito.net/challenge/en-ner-conll-2003.

Przykładowy przykład uczący (xzcat train.tsv.xz| head -n 1):

O O B-MISC I-MISC O O O O O B-LOC O B-LOC O O O O O O O O O O O B-MISC I-MISC O O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER I-PER O B-LOC O O O O O B-PER I-PER O O B-LOC O O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O B-LOC O B-LOC O O O O O O B-PER I-PER O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O O O O B-PER I-PER I-PER O B-LOC O O O O O O B-PER I-PER O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O O O O B-PER I-PER O B-LOC O O O O O O B-PER I-PER O B-LOC O O O O O B-PER I-PER O B-LOC O B-LOC O O O O O B-PER I-PER O O O O O GOLF - BRITISH MASTERS THIRD ROUND SCORES . NORTHAMPTON , England 1996-08-30 Leading scores after the third round of the British Masters on Friday : 211 Robert Allenby ( Australia ) 69 71 71 212 Pedro Linhart ( Spain ) 72 73 67 216 Miguel Angel Martin ( Spain ) 75 70 71 , Costantino Rocca ( Italy ) 71 73 72 217 Antoine Lebouc ( France ) 74 73 70 , Ian Woosnam 70 76 71 , Francisco Cea ( Spain ) 70 71 76 , Gavin Levenson ( South Africa ) 66 75 76 218 Stephen McAllister 73 76 69 , Joakim Haeggman ( Swe ) 71 77 70 , Jose Coceres ( Argentina ) 69 78 71 , Paul Eales 75 71 72 , Klas Eriksson ( Sweden ) 71 75 72 , Mike Clayton ( Australia ) 69 76 73 , Mark Roe 69 71 78 219 Eamonn Darcy ( Ireland ) 74 76 69 , Bob May ( U.S. ) 74 75 70 , Paul Lawrie 72 75 72 , Miguel Angel Jimenez ( Spain ) 74 72 73 , Peter Mitchell 74 71 75 , Philip Walton ( Ireland ) 71 74 74 , Peter O'Malley ( Australia ) 71 73 75 220 Barry Lane 73 77 70 , Wayne Riley ( Australia ) 71 78 71 , Martin Gates 71 77 72 , Bradley Hughes ( Australia ) 73 75 72 , Peter Hedblom ( Sweden ) 70 75 75 , Retief Goosen ( South Africa ) 71 74 75 , David Gilford 69 74 77 .

W pierwszym polu oczekiwany wynik zapisany za pomocą notacji BIO.

Jako metrykę używamy F1 (z pominięciem tagu O)

Metryka F1

Etykietowanie za pomocą klasyfikacji wieloklasowej

Można potraktować problem etykietowania dokładnie tak jak problem klasyfikacji wieloklasowej (jak w przykładzie klasyfikacji dyscyplin sportowych powyżej), tzn. rozkład prawdopodobieństwa możliwych etykiet uzyskujemy poprzez zastosowanie prostej warstwy liniowej i funkcji softmax:

$$p(l^k=j) = s(W\vec{v}(t^k))_j = \frac{e^{(W\vec{v}(t^k))_j}}{Z},$$

gdzie $\vec{v}(t^k)$ to reprezentacja wektorowa tokenu $t^k$. Zauważmy, że tutaj (w przeciwieństwie do klasyfikacji całego tekstu) reprezentacja wektorowa jest bardzo uboga: wektor one-hot! Taki klasyfikator w ogóle nie będzie brał pod uwagę kontekstu, tylko sam wyraz, więc tak naprawdę zdegeneruje się to do zapamiętania częstości etykiet dla każdego słowa osobno.

Bogatsza reprezentacja słowa

Można spróbować uzyskać bogatszą reprezentację dla słowa biorąc pod uwagę na przykład:

• długość słowa
• kształt słowa (_word shape), np. czy pisany wielkimi literami, czy składa się z cyfr itp.
• n-gramy znakowe wewnątrz słowa (np. słowo _Kowalski można zakodować jako sumę wektorów trigramów znakówych $\vec{v}(Kow) + \vec{v}(owa) + \vec{v}(wal) + \vec{v}(als) + \vec{v}(lsk) + + \vec{v}(ski)$

Cały czas nie rozpatrujemy jednak w tej metodzie kontekstu wyrazu. (_Renault w pewnym kontekście może być nazwą firmy, w innym — nazwiskiem).

Reprezentacja kontekstu

Za pomocą wektora można przedstawić nie pojedynczy token $t^k$, lecz cały kontekst, dla _okna o długości $c$ będzie to kontekst $t^{k-c},\dots,t^k,\dots,t^{k+c}$. Innymi słowy klasyfikujemy token na podstawie jego samego oraz jego kontekstu:

$$p(l^k=j) = \frac{e^{(W\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}))_j}}{Z_k}.$$

Zauważmy, że w tej metodzie w ogóle nie rozpatrujemy sensowności sekwencji wyjściowej (etykiet), np. może być bardzo mało prawdopodobne, że bezpośrednio po nazwisku występuje data.

Napiszmy wzór określający prawdopodobieństwo całej sekwencji, nie tylko pojedynczego tokenu. Na razie będzie to po prostu iloczyn poszczególnych wartości.

$$p(l) = \prod_{k=1}^K \frac{e^{(W\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}))_{l^k}}}{Z_k} = \frac{e^{\sum{k=1}^K (W\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}){l^k})}}{\prod{k=1}^K Z_k} $$

Reprezentacja kontekstu może być funkcją embeddingów wyrazów (zakładamy, że embedding nie zależy od pozycji słowa).

$$\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}) = f(\vec{E}(t^{k-c}),\dots,\vec{E}(t^k),\dots,\vec{E}({t^{k+c}})$$

Warunkowe pola losowe

Warunkowe pola losowe (_Conditional Random Fields, CRF) to klasa modeli, które pozwalają uwzględnić zależności między punktami danych (które można wyrazić jako graf). Najprostszym przykładem będzie prosty graf wyrażający „następowanie po” (czyli sekwencje). Do poprzedniego wzoru dodamy składnik $V_{i,j}$ (który można interpretować jako macierz) określający prawdopodobieństwo, że po etykiecie o numerze $i$ wystąpi etykieta o numerze $j$.

Pytanie: Czy macierz $V$ musi być symetryczna? Czy $V_{i,j} = V_{j,i}$? Czy jakieś specjalne wartości występują na przekątnej?

Macierz $V$ wraz z macierzą $W$ będzie stanowiła wyuczalne wagi w naszym modelu.

Wartości $V_{i,j}$ nie stanowią bezpośrednio prawdopodobieństwa, mogą przyjmować dowolne wartości, które będę normalizowane podobnie, tak jak to się dzieje w funkcji Softmax.

W takiej wersji warunkowych pól losowych otrzymamy następujący wzór na prawdopodobieństwo całej sekwencji.

$$p(l) = \frac{e^{\sum_{k=1}^K (W\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}))_{l^k} + \sum{k=1}^{K-1} V_{l^k,l^{k+1}}}}{\prod_{k=1}^K Z_k}$$

Algorytm Viterbiego

W czasie inferencji mamy ustalone wagi funkcji $\vec{v}(\dots)$ oraz macierz $V$. Szukamy sekwencji $y$ która maksymalizuje prawdopodobieństwo estymowane przez model:

$$y = \underset{l}{\operatorname{argmax}} \hat{p}(l|t^1,\dots,t^K)$$

Naiwne podejście polegające na obliczeniu prawdopodobieństw wszystkich możliwych sekwencji miałoby nieakceptowalną złożoność czasową $O(|L|^K)$.

Na szczęście, możemy użyć algorytmu Viterbiego o lepszej złożoności obliczeniowej, algorytmu opartego na idei programowania dynamicznego.

W algorytmie będziemy wypełniać dwuwymiarowe tabele $s[i, j]$ i $b[i, j]$:

• $s[i, j]$ — będzie zawierać maksymalne prawdopodobieństwo (właściwie: nieznormalizowaną wartość, która jest monotoniczna względem prawdopodobieństwa) dla ciągów o długości $i$ zakończonych etykietą $l_j$,
• $b[i, j]$ — będzie zawierać „wskaźnik” wsteczny (_backpointer) do podciągu o długości $i-1$, dla którego razem z $l_j$ jest osiągana maksymalna wartość $s[i, j]$.

Inicjalizacja:

• $s[1, j] = (W\vec{v}(t^k,\dots,t^{k+c}))_j$,
• $b[1, j]$ — nie musimy wypełniać tej wartości.

Dla $i > 1$ i dla każdego $j$ będziemy teraz szukać:

$$\underset{q \in \{1,\dots,|V|\}}{\operatorname{max}} s[i-1, q] + (W\vec{v}(t^{k-c},\dots,t^k,\dots,t^{k+c}))_j + V{q, j}$$

Tę wartość przypiszemy do $s[i, j]$, z kolei do $b[i, j]$ — indeks $q$, dla którego ta największa wartość jest osiągnięta.

Najpierw obliczenia wykonujemy wprzód wypełniając tabelę dla coraz większych wartości $j$. W ten sposób otrzymamy największą wartość (nieznormalizowanego) prawdopodobieństwa:

$$\underset{q \in \{1,\dots,|V|\}}{\operatorname{max}} s[K, q]$$

oraz ostatnią etykietę:

$$y^K = \underset{q \in \{1,\dots,|V|\}}{\operatorname{argmax}} s[K, q]$$

Aby uzyskać cały ciąg, kierujemy się _wstecz używając wskaźników:

$$y^i = b[i, y^{i+1}]$$

Złożoność obliczeniowa

Zauważmy, że rozmiar tabel $s$ i $b$ wynosi $K \times |L|$, a koszt wypełnienia każdej komórki to $|L|$, a zatem złożoność algorytmu jest wielomianowa: $O(K|L|^2)$.

Pytanie: Czy gdyby uzależnić etykietę nie tylko od poprzedniej etykiety, lecz również od jeszcze wcześniejszej, to złożoność obliczeniowa byłaby taka sama?

Przykład

Rozpatrzmy uproszczony przykład tagowania częściami mowy:

• słownik $V=\{\mathit{Ala}, \mathit{powieść}, \mathit{ma}\}$,
• zbiór etykiet $L=\{\mathit{C}, \mathit{P}, \mathit{R}\}$,
• kontekst nie jest uwzględniany ($c = 0$).

(To, że liczba słów i etykiet jest taka sama, jest przypadkowe, nie ma znaczenia)

Zakładamy, że słowa reprezentujemy wektorowo za pomocą prostej reprezentacji one-hot.

import torch

vocab = ['Ala', 'ma', 'powieść']
labels = ['C', 'P', 'R']

onehot = {
  'Ala': torch.tensor([1., 0., 0.]),
  'ma': torch.tensor([0., 1., 0.]),
  'powieść': torch.tensor([0., 0., 1.])
  }

onehot['ma']

# Out[2]:
tensor([0., 1., 0.])

Przyjmijmy, że w czasie uczenia zostały ustalone następujące wartości macierzy $W$ i $V$ (samego procesu uczenia nie pokazujemy tutaj):

import torch
import torch.nn as nn

matrixW = torch.tensor(
   [[-1., 3.0, 3.0],
    [0., 2.0, -2.0],
    [4., -2.0, 3.0]])

# rozkład prawdopodobieństwa, gdyby patrzeć tylko na słowo
nn.functional.softmax(matrixW @ onehot['powieść'], dim=0)

# Out[9]:
tensor([0.4983, 0.0034, 0.4983])

import torch
import torch.nn as nn

matrixV = torch.tensor(
   [[-0.5, 1.5, 2.0],
    [0.5, 0.8, 2.5],
    [2.0, 0.8, 0.2]])

# co występuje po przymiotniku? - rozkład prawdopodobieństwa
nn.functional.softmax(matrixV[1], dim=0)

# Out[10]:
tensor([0.1027, 0.1386, 0.7587])

Algorytm Viterbiego:

d = ['Ala', 'ma', 'powieść']

s = []
b = []

# inicjalizacja
s.append(matrixW @ onehot[d[0]])
b.append(None)

# wprzód
i = 1
os = []
ob = []
for j in range(0, len(labels)):
  z = s[i-1] + matrixV[:,j] + matrixW @ onehot[d[i]]

  ns = torch.max(z).item()
  nb = torch.argmax(z).item()

  os.append(ns)
  ob.append(nb)

os

# Out[16]:
[4.0, 3.5, 4.5]