wko/wko-02.ipynb

Widzenie komputerowe

02. Operacje binarne na obrazach [laboratoria]

Andrzej Wójtowicz (2021)

Progowanie

Podczas pracy z obrazami często potrzebne jest operowanie na obrazach, które przyjmują tylko dwie skrajne wartości. Po operacji tzw. progowania (ang. _thresholding) na obrazie będziemy mieli piksele czarne o wartości 0 lub białe o wartości 255 (lub 1, w zależności od tego na jakim typie danych i w jakiej dziedzinie operujemy).

Na początku załadujmy niezbędne biblioteki.

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

Podczas tych zajęć skupimy się na ręcznym progowaniu. Jeśli dla obrazu w skali odcieni szarości chcielibyśmy w naszym kodzie uzyskać obraz binarny, to moglibyśmy hipotetycznie wybrać jedną z trzech opcji:

1. przejść w pętli po wszystkich pikselach, sprawdzić czy wartość danego piksela jest mniejsza od wybranej wartości progowej i na tej podstawie ustawić nowy piksel jako czarny lub biały,
2. użyć biblioteki _NumPy (i przy pomocy wektoryzacji stworzyć macierz binarną),
3. użyć biblioteki _OpenCV.

W tym miejscu nie będziemy co prawda robili eksperymentu, jednak co do zasady mając do wyboru gotowe zoptymalizowane biblioteki, zdecydowanie _nie powinniśmy implementować algorytmów od podstaw (no chyba że podczas zajęć uczymy się mechaniki danych algorytmów; na produkcji raczej będziemy preferowali gotowe rozwiązania). Różnica w wydajności między naiwną ręczną implementacją a użyciem gotowej biblioteki może być, lekko licząc, kilkudziesięciokrotna.

Wykorzystajmy na początek funkcję cv2.threshold() do zwykłego progowania z progiem ustalonym na 100:

img = cv.imread("img/lena.png", cv.IMREAD_GRAYSCALE)
_, img_bin = cv.threshold(img, 100, 255, cv.THRESH_BINARY)

plt.figure(figsize=[10,10])
plt.subplot(121) 
plt.imshow(img, cmap='gray')
plt.title("Grayscale")
plt.subplot(122)
plt.imshow(img_bin, cmap='gray')
plt.title("Binary");

Istnieją również inne metody ręcznego progowania, które np. przycinają wartości do progu (w dokumentacji znajdują się wzory i przykładowe wykresy opisujące poszczególne typy operacji). Poniżej możemy zobaczyć wynik dla tych operacji:

_, img_bin = cv.threshold(img, 100, 255, cv.THRESH_BINARY)
_, img_bin_inv = cv.threshold(img, 100, 255, cv.THRESH_BINARY_INV)
_, img_trunc = cv.threshold(img, 100, 255, cv.THRESH_TRUNC)
_, img_to_zero = cv.threshold(img, 100, 255, cv.THRESH_TOZERO)
_, img_to_zero_inv = cv.threshold(img, 100, 255, cv.THRESH_TOZERO_INV)

images = (img, img_bin, img_bin_inv, img_trunc, img_to_zero, img_to_zero_inv)
titles = ("Grayscale", "Binary", "Binary Inverse", "Truncate", "To Zero", "To Zero Inverse")

plt.figure(figsize=[15,10])

for i, (image, title) in enumerate(zip(images, titles)):
    plt.subplot(231+i)
    plt.imshow(image, cmap='gray')
    plt.title(title)
    plt.colorbar()

Spójrzmy na słupki z zakresami wartości. Możemy zauważyć, że dla poszczególnych obrazów wartości minimalne i maksymalne biblioteka Matplotlib automatycznie przeskalowała do skrajnych wartości dla bieli i czerni. Aby na etapie wyświetlania usunąć to przekłamanie, musimy nieco zmienić funkcję matplotlib.pyplot.imshow() podając prawdziwe zakresy wartości:

plt.figure(figsize=[15,10])

for i, (image, title) in enumerate(zip(images, titles)):
    plt.subplot(231+i)
    plt.imshow(image, cmap='gray', vmin=0, vmax=255)
    plt.title(title)
    plt.colorbar()

Operacje morfologiczne

Morfologia matematyczna jest narzędziem, które pozwala m.in. na uzupełnianie ubytków w uszkodzonych/zniekształconych obrazach lub wyciszanie (a czasem i usuwanie) prostych kształtów. Na początku omówimy proste operacje typu erozja i dylacja, a następnie ich złożenie. Dodajmy, że operacje te działają zasadniczo na wszystkich typach obrazów (nie tylko binarnych).

Element strukturyzujący, erozja i dylacja

Na początku będziemy potrzebowali tzw. element strukturyzujący. Jest to binarna maska (mała macierz), najczęściej o nieparzystym wymiarze i zawierająca jakiś prosty, regularny kształt. Kształt ten może być dowolny, jednak w praktyce wykorzystywanych jest kilka standardowych. Do łatwego uzyskania elementu użyjemy funkcji cv.getStructuringElement().

kernel_ellipse = cv.getStructuringElement(cv.MORPH_ELLIPSE, (7, 7))
plt.imshow(kernel_ellipse, cmap='gray');

No, powiedzmy, że jest to elipsa ;) Tutaj użyliśmy dość dużego elementu o wymariach 7 na 7, jednak w praktyce może być on mniejszy.

W jaki sposób możemy wykorzystać taki element strukturyzujący? Element strutkruryzujący jest maską binarną, którą możemy _przyłożyć dla każdego piksela jakiegoś obrazu (najczęściej przykłada się go centralnie do piksela). Białe piksele maski mówią nam które sąsiadujące piksele powinniśmy wziąć w danym momencie pod uwagę. Mając wartości tych pikseli, możemy policzyć ich wartość minimalną (erozja) lub maksymalną (dylacja) i ustawić w nowym obrazie na współrzędznych danego piksela. Wykorzystuje się tutaj odpowiednio funkcje cv.erode() i cv.dilate(). Poniżej możemy zobaczyć działanie na klasycznym przykładzie z monetami:

coins = cv.imread("img/coins.png", cv.IMREAD_GRAYSCALE)
_, coins_bin = cv.threshold(coins, 125, 255, cv.THRESH_BINARY)

coins_eroded = cv.erode(coins_bin, kernel_ellipse, iterations=1)
coins_dilated = cv.dilate(coins_bin, kernel_ellipse, iterations=1)

plt.figure(figsize=[10,8])
plt.subplot(221)
plt.imshow(coins, cmap='gray')
plt.title("Grayscale")
plt.subplot(222)
plt.imshow(coins_bin, cmap='gray')
plt.title("Binary")
plt.subplot(223)
plt.imshow(coins_eroded, cmap='gray')
plt.title("Eroded")
plt.subplot(224)
plt.imshow(coins_dilated, cmap='gray')
plt.title("Dilated");

Możemy zauważyć, że zastosowanie erozji spowodowało wypełnienie w większym lub mniejszym stopniu dziur w zbinaryzowanych monetach. Z kolei dylacja spowodowała prawie zaniknięcie obrazu. Użyliśmy tutaj jednej iteracji, jednak możliwe jest kilkukrotne wykonanie erozji lub dylacji.

Poniżej możemy zobaczyć, że erozja i dylacja są w pewien sposób komplementarne:

coins = cv.imread("img/coins.png", cv.IMREAD_GRAYSCALE)
_, coins_bin = cv.threshold(coins, 125, 255, cv.THRESH_BINARY_INV)

coins_eroded = cv.erode(coins_bin, kernel_ellipse, iterations=1)
coins_dilated = cv.dilate(coins_bin, kernel_ellipse, iterations=1)

plt.figure(figsize=[10,8])
plt.subplot(221)
plt.imshow(coins, cmap='gray')
plt.title("Grayscale")
plt.subplot(222)
plt.imshow(coins_bin, cmap='gray')
plt.title("Binary")
plt.subplot(223)
plt.imshow(coins_eroded, cmap='gray')
plt.title("Eroded")
plt.subplot(224)
plt.imshow(coins_dilated, cmap='gray')
plt.title("Dilated");

Element strukturyzujący w kształcie elipsy całkiem dobrze zadziałał w przypadku usunięcia dziur w owalnych kształtach. Z drugiej strony musimy być świadomi, że inne, arbitralne kształty mogą być przydatne w specjalnych zastosowaniach (np. pionowe lub ukośne linie/kreski).

Otwarcie i zamknięcie

Złożenie operacji dylacji i erozji może posłużyć np. do uzupełnienia przerw między kształtami lub wyciszenia drobnych szumów. Tzw. _otwarcie dotyczy erozji, po której następuje dylacja, co w konsekwencji usuwa białe plamy i przerwy. Z kolei tzw. zamknięcie to dylacja, po której następuje erozja, i taka operacja usuwa czarne plamy i przerwy. Jeśli interesuje nas wypełnienie przerw, to takie złożenia operacji nie będą powodowały rozrastania obiektów. Użyjemy tutaj funkcji cv.morphologyEx().

coins_opened = cv.morphologyEx(coins_bin, cv.MORPH_OPEN, kernel_ellipse, iterations=1)

plt.figure(figsize=[10,10])

plt.subplot(121)
plt.imshow(coins_bin, cmap='gray')
plt.title("Binary")
plt.subplot(122)
plt.imshow(coins_opened, cmap='gray')
plt.title("Opening");

Zadanie 1

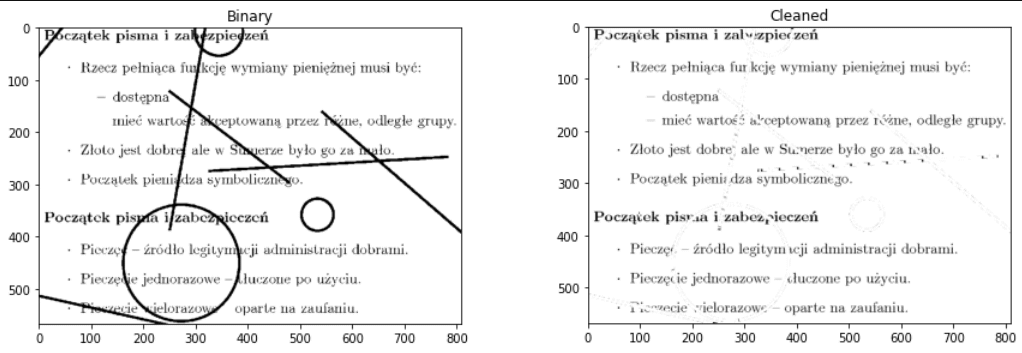
Wczytaj obraz text_no_ocr.png, który zawiera fragment starych notatek (z przedmiotu "E-gospodarka" dra Michała Rena) posiadających zabezpieczenie przed dalszym przetwarzaniem. Spróbuj usunąć niechciane kształty (wynik nie musi być dokładny - może uzyskasz lepszy efekt?).

kernel = cv.getStructuringElement(cv.MORPH_CROSS , (5, 5)) 
plt.imshow(kernel, cmap="gray")

<matplotlib.image.AxesImage at 0x127d14f24c8>

img_path = "img/text_no_ocr.png"
coins = cv.imread(img_path, cv.IMREAD_GRAYSCALE)
_, coins_bin = cv.threshold(coins, 100, 255, cv.THRESH_BINARY)

coins_eroded = cv.erode(coins_bin, kernel, iterations=1)
# coins_dilated = cv.dilate(coins_bin, kernel, iterations=1)
coins_dilated = np.invert(cv.morphologyEx(coins_bin, cv.MORPH_BLACKHAT, kernel))


plt.figure(figsize=[10,8])
plt.subplot(221)
plt.imshow(coins, cmap='gray')
plt.title("Grayscale")
plt.subplot(222)
plt.imshow(coins_bin, cmap='gray')
plt.title("Binary")
plt.subplot(223)
plt.imshow(coins_eroded, cmap='gray')
plt.title("Eroded")
plt.subplot(224)
plt.imshow(coins_dilated, cmap='gray')
plt.title("BLACKHAT");

Analiza połączonych komponentów

Jeśli na naszym obrazie binarnym posiadamy zwarte grupy obiektów, to możemy im nadać etykiety i je policzyć. Na poniższym zdjęciu możemy policzyć litery napisu:

bologna = cv.imread("img/bologna.png", cv.IMREAD_GRAYSCALE)
_, bologna_bin = cv.threshold(bologna, 127, 255, cv.THRESH_BINARY)

plt.figure(figsize=[10,5])

plt.imshow(bologna_bin, cmap='gray');

Do nadania etykiet użyjemy funkcji cv.connectedComponents():

_, bologna_labels = cv.connectedComponents(bologna_bin)

plt.figure(figsize=[10,5])

plt.imshow(bologna_labels, cmap='gray')
plt.colorbar();

Zauważmy, że wynikowy obraz ma 8 etykiet, gdzie 0 oznacza tło, a kolejne siedem są przypisane do poszczególnych liter. Możemy wyświetlić poszczególne fragmenty obrazu dotyczące danej etykiety:

bologna_n = bologna_labels.max()

plt.figure(figsize=[12,7])

for i in range(bologna_n+1):
    plt.subplot(331+i)
    plt.imshow(bologna_labels==i, cmap='gray')
    plt.title(f"Label: {i}")

Do wygodnego wyświetlenia pokolorowanych etykiet możemy użyć map kolorów. Pracując z biblioteką Matplotlib możemy wyświetlić taki obraz wprost i użyć ew. odpowiedniej mapy kolorów, np.:

plt.figure(figsize=[17,5])

plt.subplot(131)
plt.imshow(bologna_labels)
plt.title("Default")
plt.colorbar()
plt.subplot(132)
plt.imshow(bologna_labels, cmap='gray')
plt.colorbar()
plt.title("Gray")
plt.subplot(133)
plt.imshow(bologna_labels, cmap='inferno')
plt.colorbar()
plt.title("Inferno");

Biblioteka OpenCV również posiada obsługę map kolorów, co może być pomocne gdybyśmy chcieli np. wyeksportować obraz. Na początku możemy przekonwertować obraz do przedziału [0; 255] (znajdujemy minimalną i maksymalną wartość przy pomocy cv.minMaxLoc()), a następnie używamy funkcji cv.applyColorMap() podając wybraną mapę i otrzymując obraz BGR, np.:

val_min, val_max, _, _ = cv.minMaxLoc(bologna_labels)
bologna_labels_norm = 255 * (bologna_labels - val_min)/(val_max - val_min)
bologna_labels_norm = np.uint8(bologna_labels_norm)

bologna_labels_turbo = cv.applyColorMap(bologna_labels_norm, cv.COLORMAP_TURBO)
plt.imshow(bologna_labels_turbo[:,:,::-1])
plt.title("Turbo");

print(cv.__version__)

4.6.0

Kontury

W widzeniu komputerowym bardzo często chcemy nie tylko znaleźć pewne obiekty, ale również zaznaczyć ich obrys (kontury). Poniżej znajduje się kilka przykładów - będziemy co prawda działali na obrazie w skali odcieni szarości, aczkolwiek w pewnych zastosowaniach lepsze efekty dałaby praca na obrazie czarno-białym.

shapes = cv.imread("img/shapes.png", cv.IMREAD_COLOR)
shapes_gray = cv.cvtColor(shapes, cv.COLOR_BGR2GRAY)

plt.figure(figsize=[10,5])

plt.subplot(121)
plt.imshow(shapes[:,:,::-1])
plt.title("Original")
plt.subplot(122)
plt.imshow(shapes_gray, cmap='gray')
plt.title("Grayscale");

Przy pomocy cv.findContours() uzyskujemy kontury obiektów oraz opcjonalną macierz opisującą ich hierarchię. Drugi parametr funkcji opisuje sposób wyznaczania konturów, a trzeci algorytm aproksymacji konturów.

shapes_contours, _ = cv.findContours(shapes_gray, cv.RETR_LIST, cv.CHAIN_APPROX_SIMPLE)
print(f"No. of contours: {len(shapes_contours)}")

No. of contours: 11

Przy pomocy cv.drawContours() możemy nanieść kontury na obraz. Zauważmy, że mamy tutaj oznaczone zewnętrzne i wewnętrzne kontury:

shapes_with_contours = shapes.copy()

cv.drawContours(shapes_with_contours, shapes_contours, -1, (255,255,0), 2)

plt.figure(figsize=[10,5])
plt.imshow(shapes_with_contours[:,:,::-1]);

Możemy również ograniczyć się tylko do zewnętrznych konturów (parametr cv.RETR_EXTERNAL):

shapes_contours, _ = cv.findContours(shapes_gray, cv.RETR_EXTERNAL, cv.CHAIN_APPROX_SIMPLE)
print(f"No. of contours: {len(shapes_contours)}")
shapes_with_contours = shapes.copy()

cv.drawContours(shapes_with_contours, shapes_contours, -1, (255,255,0), 2)

plt.figure(figsize=[10,5])
plt.imshow(shapes_with_contours[:,:,::-1]);

No. of contours: 9

Poniżej mamy zaznaczony obrys konturu wybranego obiektu, np. o indeksie 5:

shapes_with_contours = shapes.copy()

cv.drawContours(shapes_with_contours, shapes_contours, 5, (255,255,0), 2)

plt.figure(figsize=[10,5])
plt.imshow(shapes_with_contours[:,:,::-1]);

Poniżej możemy zobaczyć jak przy pomocy tzw. momentów są wyliczane środki ciężkości poszczególnych konturów. Każdy kontur jest również opisany żółtą etykietą liczbową, ale w związku z tym, że czasem mamy kontur zewnętrzny i wewnętrzny blisko siebie, to niektóre etykiety nakładają się na siebie. Dodatkowo, tym razem kontury wykryjemy z informacją o drzewiastej hierarchii (parametr cv.RETR_TREE, za chwilę opiszemy co tam się znajduje).

shapes_contours, shapes_hierarchy = cv.findContours(shapes_gray, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
shapes_with_contours = shapes.copy()

cv.drawContours(shapes_with_contours, shapes_contours, -1, (255,255,0), 2)

for idx, contour in enumerate(shapes_contours):
    M = cv.moments(contour)
    x = int(round(M["m10"]/M["m00"]))
    y = int(round(M["m01"]/M["m00"]))
    
    cv.circle(shapes_with_contours, (x,y), 5, (255,255,255), -1)
    cv.putText(shapes_with_contours, str(idx), (x+10, y+10), cv.FONT_HERSHEY_SIMPLEX, 1, (0, 200, 255), 2)
    
plt.figure(figsize=[10,5])
plt.imshow(shapes_with_contours[:,:,::-1]);

W zmiennej shapes_hierarchy mamy macierz opisującą hierarchię konturów. Dla każdego wiersza (konturu) kolejne kolumny opisują odpowiednio: indeks następnego konturu, indeks poprzedniego konturu, indeks pierwszego dziecka oraz indeks rodzica (wartość ujemna oznacza, że dane pole nie ma zastosowania).

print(shapes_hierarchy)

[[[ 1 -1 -1 -1]
  [ 2  0 -1 -1]
  [ 3  1 -1 -1]
  [ 5  2  4 -1]
  [-1 -1 -1  3]
  [ 6  3 -1 -1]
  [ 7  5 -1 -1]
  [ 8  6 -1 -1]
  [ 9  7 -1 -1]
  [-1  8 10 -1]
  [-1 -1 -1  9]]]

Przy pomocy cv.contourArea() i cv.arcLength() możemy policzyć odpowiednio pole powierzchni i obwód kształtu:

for idx, contour in enumerate(shapes_contours):
    area = cv.contourArea(contour)
    perimeter = round(cv.arcLength(contour, True), 1)
    print(f"Contour id {idx: >2}: area = {area: >6}, perimeter = {perimeter: >5}")

Contour id  0: area = 1063.0, perimeter = 161.4
Contour id  1: area = 8017.5, perimeter = 390.0
Contour id  2: area =  375.0, perimeter = 133.0
Contour id  3: area = 1750.0, perimeter = 170.0
Contour id  4: area =  556.0, perimeter =  95.7
Contour id  5: area = 2917.0, perimeter = 244.7
Contour id  6: area =  729.5, perimeter = 185.6
Contour id  7: area = 1922.0, perimeter = 175.7
Contour id  8: area =  380.5, perimeter =  73.4
Contour id  9: area = 2596.5, perimeter = 191.6
Contour id 10: area =  407.0, perimeter =  75.6

Dla znalezionych kształtów często chcemy wyznaczyć ramkę ograniczającą i możemy to zrobić na kilka sposobów. Poniżej przy pomocy cv.boundingRect() i cv.rectangle() nanosimy prostokąty:

shapes_with_bb = shapes_with_contours.copy()
for contour in shapes_contours:
    x,y,w,h = cv.boundingRect(contour)
    cv.rectangle(shapes_with_bb, (x,y), (x+w,y+h), (255,0,255), 2)
    
plt.figure(figsize=[10,5])
plt.imshow(shapes_with_bb[:,:,::-1]);

Czasami wygodniej jest umieścić minimalny obrys prostokąta, co możemy uzyskać przy pomocy cv.minAreaRect() i cv.boxPoints():

shapes_with_bb = shapes_with_contours.copy()
for contour in shapes_contours:
    rect = cv.minAreaRect(contour)
    box_points = np.int0(cv.boxPoints(rect))
    cv.drawContours(shapes_with_bb, [box_points], -1, (255,0,255), 2)
    
plt.figure(figsize=[10,5])
plt.imshow(shapes_with_bb[:,:,::-1]);

Poniżej mamy przykład z okręgiem przy pomocy cv.minEnclosingCircle():

shapes_with_bb = shapes_with_contours.copy()
for contour in shapes_contours:
    (x,y), radius = cv.minEnclosingCircle(contour)
    cv.circle(shapes_with_bb, (int(x),int(y)), int(round(radius)), (255,0,255), 2)
    
plt.figure(figsize=[10,5])
plt.imshow(shapes_with_bb[:,:,::-1]);

Możemy również umieścić elipsy przy pomocy cv.fitEllipse(), ale w tym przypadku kontur musi składać się z co najmniej 5 punktów:

shapes_with_bb = shapes_with_contours.copy()
for contour in shapes_contours:
    if len(contour) < 5:
        continue
    ellipse = cv.fitEllipse(contour)
    cv.ellipse(shapes_with_bb, ellipse, (255,0,255), 2)
    
plt.figure(figsize=[10,5])
plt.imshow(shapes_with_bb[:,:,::-1]);

Wykrywanie obszarów/plam

Do wykrywania obszarów/plam (ang. _blobs) posiadających wspólne cechy (np. rozmiar, kształt, wartości pikseli) możemy użyć cv.SimpleBlobDetector_create(), a następnie używamy metody detect(). W poniższym przykładzie użyjemy domyślnych wartości detektora.

blobs_gray = cv.imread("img/blobs.png", cv.IMREAD_GRAYSCALE)
 
blob_detector = cv.SimpleBlobDetector_create()

keypoints = blob_detector.detect(blobs_gray)

blobs_color = cv.cvtColor(blobs_gray, cv.COLOR_GRAY2BGR)
 
for kp in keypoints:
    x, y = kp.pt
    x = int(round(x))
    y = int(round(y))

    radius = int(round(kp.size/2))

    cv.circle(blobs_color, (x,y), radius, (0,0,255), 3)

plt.figure(figsize=[15,5])
plt.subplot(121)
plt.imshow(blobs_gray, cmap='gray')
plt.title("Grayscale")
plt.subplot(122)
plt.imshow(blobs_color[:,:,::-1])
plt.title("Blobs");

Parametry ustawia się poprzez atrybuty obiektu zwracanego przez cv.SimpleBlobDetector_Params(). Po ustawieniu parametrów obiekt z parametrami przekazuje się jako argument cv.SimpleBlobDetector_create().

Detektor działa następująco:

1. Obraz źródłowy jest przekształcany do obrazów binarnych poprzez progowanie z wartościami odcięcia od minThreshold do maxThreshold z krokiem thresholdStep.
2. Dla każdego obrazu binarnego znajdowane są połączone komponenty przy pomocy cv.findContours() oraz obliczane są współrzędne ich środków.
3. Środki z kilku obrazów binarnych są grupowane na podstawie ich współrzędnych. Te, które znajdują się blisko siebie, odpowiadają jednej plamie/obszarowi (kontroluje się to poprzez parametr minDistBetweenBlobs).
4. Na podstawie wyznaczonych wcześniej grup obliczane są końcowe współrzędne środków plam/obszarów oraz ich promienie, tak by zwrócić je jako lokalizacje i rozmiary punktów kluczowych.

Detektor dokonuje kilku filtracji zwracanych plam/obszarów. Poszczególne filtry ustawia się poprzez parametry filterBy* nadając im wartość True lub False. Można filtrować według:

1. koloru (filterByColor = True), tj. następuje porównanie intensywności środka plamy/obszaru z obrazu binarnego do wartości ustawionej w blobColor; jeśli są różne, to plama/obszar jest odfiltrowana; wartość blobColor = 0 wyodrębnia czarne plamy/obszary, a blobColor = 255 jasne,
2. powierzchni (filterByArea = True), tj. plamy/obszary mają mieć powierzchnię między minArea a maxArea; np. ustawienie minArea = 100 spowoduje odfiltrowanie plam/obszarów, których powierzchnia stanowi mniej niż 100 pikseli,
3. okrągłości (filterByCircularity = True), tj. miara okrągłości plamy/obszaru 4 * pi * pole powierzchni / obwód^2 ma być między minCircularity a maxCircularity; np. regularny sześciokąt ma większą okrągłość niż kwadrat; np. okrąg ma miarę 1.0, a kwadrat ok. 0.785,
4. inercji (filterByInertia = True), tj. jej wartość ma się znaleźć między minInertiaRatio a maxInertiaRatio; miara ta określa jak bardzo wydłużony jest dany kształt, np. dla okręgu wartość ta wynosi 1, dla elipsy mieści się w przedziale od 0 do 1, a dla linii wynosi 0; aby odfiltrować po inercji można ustawić 0 ≤ minInertiaRatio ≤ 1 oraz maxInertiaRatio ≤ 1,
5. wypukłości (filterByConvexity = True), tj. pole powierzchni / pole powierzchni otoczki wypukłej ma być między minConvexity a maxConvexity; aby odfiltrować po wypukłości można ustawić 0 ≤ minConvexity ≤ 1 oraz maxConvexity ≤ 1.

Domyślne wartości parametrów są dostrojone do ekstrakcji ciemnych, okrągłych plam.

Poniżej znajduje się przykład skonfigurowania parametrów pod kątem progu i minimalnego pola powierzchni:

params = cv.SimpleBlobDetector_Params()
params.minThreshold = 200
params.maxThreshold = 255
params.filterByArea = True
params.minArea = 2000

blob_detector = cv.SimpleBlobDetector_create(params)

keypoints = blob_detector.detect(blobs_gray)

blobs_color = cv.cvtColor(blobs_gray, cv.COLOR_GRAY2BGR)
 
for kp in keypoints:
    x, y = kp.pt
    x = int(round(x))
    y = int(round(y))

    radius = int(round(kp.size/2))

    cv.circle(blobs_color, (x,y), radius, (0,0,255), 3)

plt.figure(figsize=[15,5])
plt.subplot(121)
plt.imshow(blobs_gray, cmap='gray')
plt.title("Grayscale")
plt.subplot(122)
plt.imshow(blobs_color[:,:,::-1])
plt.title("Blobs");

Zadanie 2

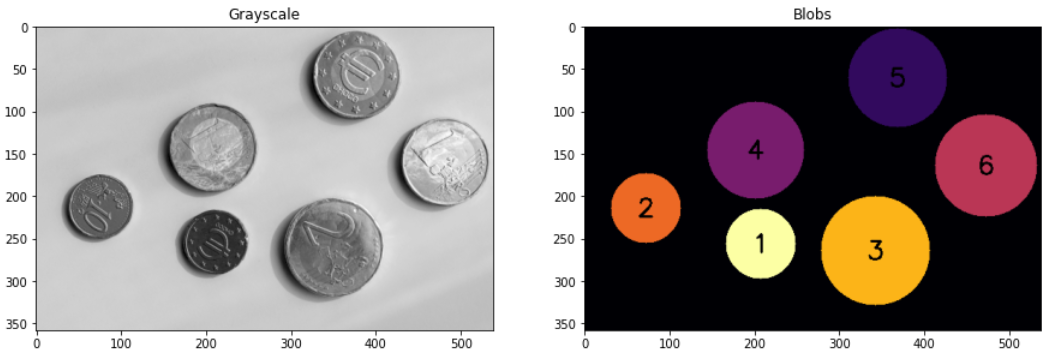
Spróbuj wykryć i oznaczyć monety z pliku img/coins.png. Przykładowy wynik znajduje się poniżej (użyto schematu kolorów _inferno, kolejność wykrytych monet nie jest istotna).

# miejsce na eksperymenty
blobs_gray = cv.imread("img/coins.png", cv.IMREAD_GRAYSCALE)

params = cv.SimpleBlobDetector_Params()
params.minThreshold = 150;
params.maxThreshold = 230;
params.filterByArea = True;
params.minArea = 50;
params.maxArea = 50000;
params.filterByConvexity = True;
params.minConvexity = 0.9;
params.maxConvexity = 1.0;

params.filterByCircularity = False;
params.filterByInertia = False;
params.filterByColor = False;
blob_detector = cv.SimpleBlobDetector_create(params)

keypoints = blob_detector.detect(blobs_gray)

blobs_color = cv.cvtColor(blobs_gray, cv.COLOR_GRAY2BGR)
 
for kp in keypoints:
    x, y = kp.pt
    x = int(round(x))
    y = int(round(y))

    radius = int(round(kp.size/2))

    cv.circle(blobs_color, (x,y), radius, (0,0,255), 3)

for idx, kp in enumerate(keypoints):
    # M = cv.moments(kp)
    x, y = kp.pt
    x = int(round(x))
    y = int(round(y))
    
    # cv.circle(shapes_with_contours, (x,y), 5, (255,255,255), -1)
    cv.putText(blobs_color, str(idx), (x+10, y+10), cv.FONT_HERSHEY_SIMPLEX, 1, (0, 200, 255), 2)

plt.figure(figsize=[15,5])
plt.subplot(121)
plt.imshow(blobs_gray, cmap='gray')
plt.title("Grayscale")
plt.subplot(122)
plt.imshow(blobs_color[:,:,::-1])
plt.title("Blobs");