5.3 KiB

Ekstrakcja informacji
13. Podejście generatywne w ekstrakcji informacji [wykład]
Filip Graliński (2021)

Ekstrakcja informacji a podejście generatywne
Podejście generatywne
Do tej pory zadanie ekstrakcji informacji traktowaliśmy jako zadanie etykietowania sekwencji, tzn. uczyliśmy system zaznaczać tokeny składające się na ekstrahowane informacje.
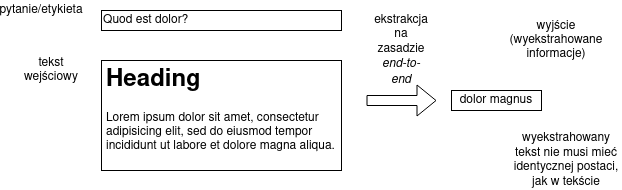
Możliwe jest inne podeście, generatywne, w którym podchodzimy do problemu ekstrakcji informacji jak do swego rodzaju tłumaczenia maszynowego — „tłumaczymy” tekst (wraz z pytaniem lub etykietą) na informację.
To podejście może się wydawać trudniejsze niż etykietowanie sekwencji, ale wystarczająco zaawansowanej architekturze sieci, jest wykonalne.
Zalety:
- informacja nie musi być dosłownie zapisana w tekście, ekstraktor może nauczyć się również normalizacji czy parafrazowania,
- nie wprowadzamy wielu kroków przetwarzania (gdzie błędy mogą się namnażać), system działa na zasadzie _end-to-end.
Atencja
Pierwsze systemu neuronowego tłumaczenia maszynowego używały siecie LSTM. Dopiero jednak dodanie tzw. atencji (_attention) umożliwiło duży przeskok jakościowy. Najpierw atencję dodano do sieci rekurencyjnych, później powstały sieci oparte wyłącznie na atencji — modele Transformer.
Idea atencji polega na tym, że sieć może kierować selektywnie „snop” uwagi na wyrazy na wejściu lub do tej pory wygenerowane wyrazy.
Mechanizm atencji korzysta z:
- z poprzedniego stanu sieci $\vec{s^{k-1}}$ (to jest „miejsce”, z którego „kierujemy” atencję),
- z wektora reprezentującego słowo $\vec{v}(t_i)$ (to jest „miejsce”, na które kierujemy atencję), gdzie $\vec{v}(t_i)$ to reprezentacja wektorowa wyrazu $t_i$ (statyczny embedding lub reprezentacja wektorowa z poprzedniej warstwy dla sieci wielowarstwowej),
aby wytworzyć wektor kontekstu $\vec{\xi^k}$ (który z kolei będzie w jakiś sposób wnosił wkład do wyliczenia nowej wartości stanu $\vec{s^k}$ lub wyjścia $y^k$.
Najpierw wyliczymy skalarne wartości atencji, tzn. liczby, które będą sygnalizowały, jak bardzo wektor $\vec{v}(t_i)$ „pasuje” do $\vec{s^{k-1}}$, w najprostszej wersji można po prostu skorzystać z iloczynu skalarnego (o ile $n=m$),
$$a(\vec{s^{k-1}}, \vec{v}(t_i)) = \vec{s^{k-1}}\vec{v}(t_i).$$
Pytanie: co jeśli $n$ nie jest równe $m$, tzn. rozmiar embeddingu nie jest równy rozmiarowi wektora stanu?
W przypadku sieci LSTM korzysta się częściej z bardziej skomplikowanego wzoru zawierającego dodatkowe wyuczalne wagi:
$$a(\vec{s^{k-1}}, \vec{v}(t_i)) = \vec{w_a}\operatorname{tanh}(W_a\vec{s^{k-1}} + U_a\vec{v}(t_i))$$
Pytanie: jakie rozmiary mają macierze $W_a$, $U_a$ i wektor $w_a$?
Powtórzmy, że wartości $a$ są wartościami skalarnymi, natomiast nie są one znormalizowane (nie sumują się do jedynki), normalizujemy je używając schematu podobnego do softmaxa:
$$\alpha_{i} = \frac{e^{a(\vec{s^{k-1}}, \vec{v}(t_i))}}{\sum_j e^{a(\vec{s^{k-1}}, \vec{v}(t_j))}}$$
Wektor kontekstu $\vec{\xi^k}$ będzie po prostu średnią ważoną wektorowych reprezentacji słów:
$$\vec{\xi^k} = \sum_i \alpha_i\vec{v}(t_i)$$
Pytanie: zasadniczo atencja jest środkiem do celu (żeby sieć się sprawniej uczyła), czy można atencja sama w sobie może być do czegoś przydatna?