s444820/aitech-eks-pub

Fork 0

forked from filipg/aitech-eks-pub

Filip Gralinski 1836dc18c1 Remove too long text material

2021-09-27 08:10:10 +02:00

192 KiB

Raw Blame History

Logo 1

Ekstrakcja informacji

3. Wyszukiwarki — TF-IDF [wykład]

Filip Graliński (2021)

Logo 2

Wyszukiwarka - szybka i sensowna

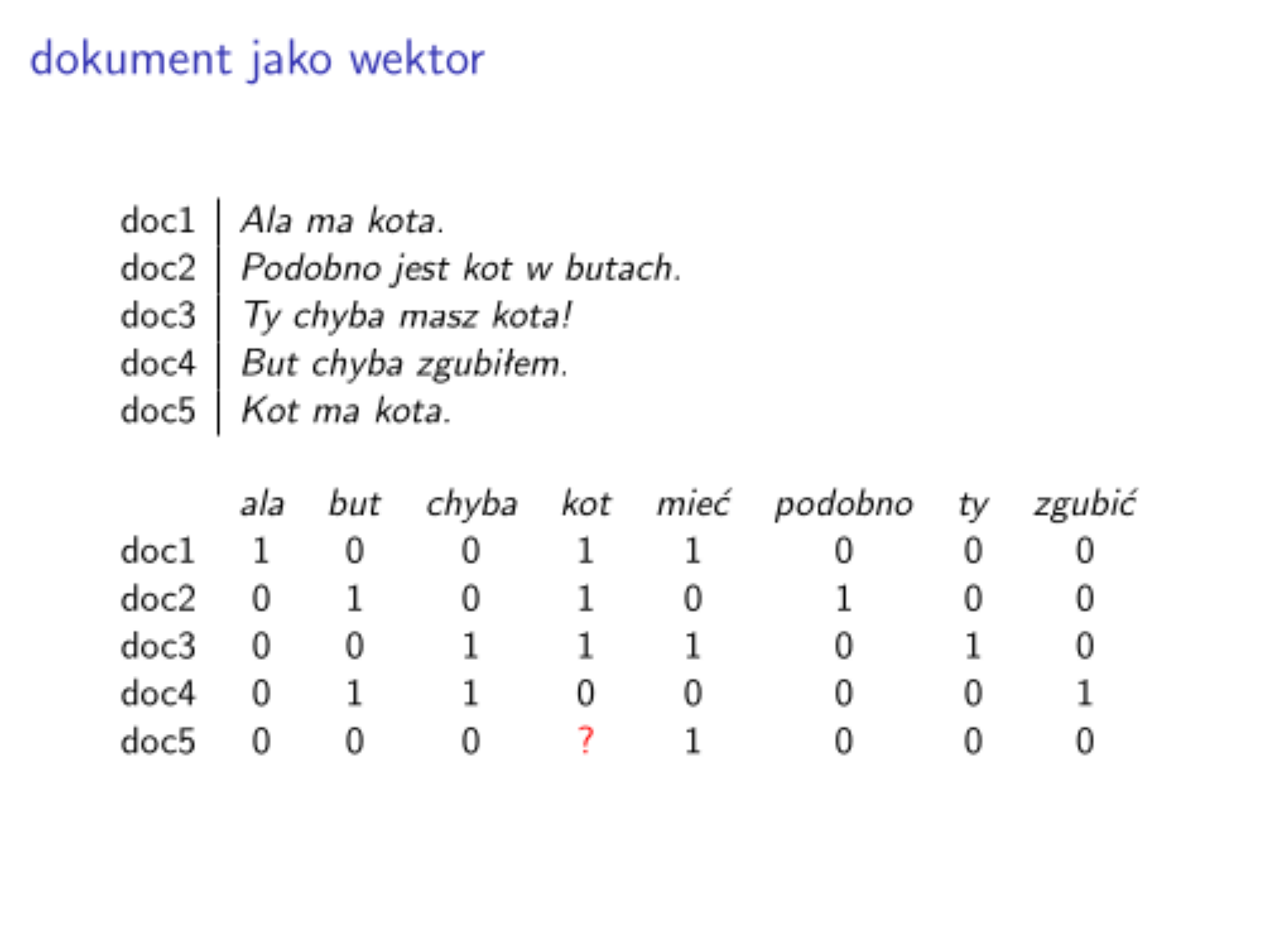
Roboczy przykład

Zakładamy, że mamy pewną kolekcję dokumentów $D = {d_1, \ldots, d_N}$. ($N$ - liczba dokumentów w kolekcji).

{-# LANGUAGE OverloadedStrings #-}

import Data.Text hiding(map, filter, zip)
import Prelude hiding(words, take)

collectionD :: [Text]
collectionD = ["Ala ma kota.", "Podobno jest kot w butach.", "Ty chyba masz kota!", "But chyba zgubiłem.", "Kot ma kota."]

-- Operator (!!) zwraca element listy o podanym indeksie
-- (Przy większych listach będzie nieefektywne, ale nie będziemy komplikować)
Prelude.head collectionD

Ala ma kota.

Wydobycie tekstu

Przykładowe narzędzia:

pdftotext
antiword
Tesseract OCR
Apache Tika - uniwersalne narzędzie do wydobywania tekstu z różnych formatów

Normalizacja tekstu

Cokolwiek robimy z tekstem, najpierw musimy go _znormalizować.

Tokenizacja

Po pierwsze musimy podzielić tekst na _tokeny, czyli wyrazapodobne jednostki. Może po prostu podzielić po spacjach?

tokenizeStupidly :: Text -> [Text]
-- words to funkcja z Data.Text, która dzieli po spacjach
tokenizeStupidly = words

tokenizeStupidly $ Prelude.head collectionD

Ala

ma

kota.

A, trzeba _chociaż odsunąć znaki interpunkcyjne. Najprościej użyć wyrażenia regularnego. Warto użyć unikodowych własności znaków i konstrukcji \p{...}.

{-# LANGUAGE QuasiQuotes #-}

import Text.Regex.PCRE.Heavy

tokenize :: Text -> [Text]
tokenize = map fst . scan [re|C\+\+|[\p{L}0-9]+|\p{P}|]

tokenize $ collectionD !! 3

But

chyba

zgubiłem

Cała kolekcja stokenizowana:

map tokenize collectionD

Ala

ma

kota

Podobno

jest

kot

butach

Ty

chyba

masz

kota

But

chyba

zgubiłem

Kot

ma

kota

Problemy z tokenizacją

Język angielski

tokenize "I use a data-base"

use

data

base

tokenize "I use a database"

use

database

tokenize "I use a data base"

use

data

base

tokenize "'I don't like Python'"

don

like

Python

tokenize "I can see the Johnes' house"

can

see

the

Johnes

house

tokenize "I do not like Python"

do

not

like

Python

tokenize "+0018 555-555-122"

tokenize "+0018555555122"

0018555555122

tokenize "Which one is better: C++ or C#?"

Which

one

is

better

C++

or

Inne języki?

tokenize "Rechtsschutzversicherungsgesellschaften wie die HUK-Coburg machen es bereits seit geraumer Zeit vor:"

Rechtsschutzversicherungsgesellschaften

wie

die

HUK

Coburg

machen

es

bereits

seit

geraumer

Zeit

vor

tokenize "今日波兹南是贸易、工业及教育的中心。波兹南是波兰第五大的城市及第四大的工业中心，波兹南亦是大波兰省的行政首府。也舉辦有不少展覽會。是波蘭西部重要的交通中心都市。"

今日波兹南是贸易

、

工业及教育的中心

。

波兹南是波兰第五大的城市及第四大的工业中心

，

波兹南亦是大波兰省的行政首府

。

也舉辦有不少展覽會

。

是波蘭西部重要的交通中心都市

。

tokenize "l'ordinateur"

ordinateur

Lematyzacja

_Lematyzacja to sprowadzenie do formy podstawowej (lematu), np. "krześle" do "krzesło", "zrobimy" do "zrobić" dla języka polskiego, "chairs" do "chair", "made" do "make" dla języka angielskiego.

Lematyzacja dla języka polskiego jest bardzo trudna, praktycznie nie sposób wykonać ją regułowo, po prostu musimy się postarać o bardzo obszerny _słownik form fleksyjnych.

Na potrzeby tego wykładu stwórzmy sobie mały słownik form fleksyjnych w postaci tablicy asocjacyjnej (haszującej).

import Data.Map as Map hiding(take, map, filter)

mockInflectionDictionary :: Map Text Text
mockInflectionDictionary = Map.fromList [
   ("kota", "kot"),
   ("butach", "but"),
   ("masz", "mieć"),
   ("ma", "mieć"),
   ("buta", "but"),
   ("zgubiłem", "zgubić")]

lemmatizeWord :: Map Text Text -> Text -> Text
lemmatizeWord dict w = findWithDefault w w dict

lemmatizeWord mockInflectionDictionary "butach"
-- a tego nie ma w naszym słowniczku, więc zwracamy to samo
lemmatizeWord mockInflectionDictionary "butami"

lemmatize :: Map Text Text -> [Text] -> [Text]
lemmatize dict = map (lemmatizeWord dict)

lemmatize mockInflectionDictionary $ tokenize $ collectionD !! 0 

lemmatize mockInflectionDictionary $ tokenize "Wczoraj kupiłem kota."

Use head

Found:

collectionD !! 0

Why Not:

head collectionD

but

butami

Ala

mieć

kot

Wczoraj

kupiłem

kot

Pytanie: Nawet w naszym słowniczku mamy problemy z niejednoznacznością lematyzacji. Jakie?

Obszerny słownik form fleksyjnych dla języka polskiego: http://zil.ipipan.waw.pl/PoliMorf?action=AttachFile&do=view&target=PoliMorf-0.6.7.tab.gz

Stemowanie

Stemowanie (rdzeniowanie) obcina wyraz do _rdzenia niekoniecznie będącego sensownym wyrazem, np. "krześle" może być rdzeniowane do "krześl", "krześ" albo "krzes", "zrobimy" do "zrobi".

stemowanie nie jest tak dobrze określone jak lematyzacja (można robić na wiele sposobów)
bardziej podatne na metody regułowe (choć dla polskiego i tak trudno)
dla angielskiego istnieją znane algorytmy stemowania, np. algorytm Portera
zob. też program Snowball z regułami dla wielu języków

Prosty stemmer "dla ubogich" dla języka polskiego to obcinanie do sześciu znaków.

poorMansStemming :: Text -> Text
poorMansStemming = Data.Text.take 6

poorMansStemming "zrobimy"
poorMansStemming "komputerami"
poorMansStemming "butach"
poorMansStemming "źdźbłami"

zrobim

komput

butach

źdźbła

_Stop words

Często wyszukiwarki pomijają krótkie, częste i nieniosące znaczenia słowa - _stop words (słowa przestankowe).

isStopWord :: Text -> Bool
isStopWord "w" = True
isStopWord "jest" = True
isStopWord "że" = True
-- przy okazji możemy pozbyć się znaków interpunkcyjnych
isStopWord w = w ≈ [re|^\p{P}+$|]

isStopWord "kot"
isStopWord "!"

False

True

removeStopWords :: [Text] -> [Text]
removeStopWords = filter (not . isStopWord)

removeStopWords $ tokenize $ Prelude.head collectionD

Ala

ma

kota

Pytanie: Jakim zapytaniom usuwanie _stop words może szkodzić? Podać przykłady dla języka polskiego i angielskiego.

Normalizacja - różności

W skład normalizacji może też wchodzić:

poprawianie błędów literowych
sprowadzanie do małych liter (lower-casing czy raczej case-folding)
usuwanie znaków diakrytycznych

toLower "ŻDŹBŁO"

żdźbło

toCaseFold "ŹDŹBŁO"

źdźbło

Pytanie: Kiedy _case-folding da inny wynik niż lower-casing? Jakie to ma praktyczne znaczenie?

Normalizacja jako całościowy proces

Najważniejsza zasada: dokumenty w naszej kolekcji powinny być normalizowane w dokładnie taki sposób, jak zapytania.

Efektem normalizacji jest zamiana dokumentu na ciąg _termów (ang. terms), czyli znormalizowanych wyrazów.

Innymi słowy po normalizacji dokument $d_i$ traktujemy jako ciąg termów $t_i^1,\dots,t_i^{|d_i|}$.

normalize :: Text -> [Text]
normalize = map poorMansStemming . removeStopWords . map toLower . lemmatize mockInflectionDictionary . tokenize

map normalize collectionD

ala

mieć

kot

podobn

kot

but

ty

chyba

mieć

kot

but

chyba

zgubić

kot

mieć

kot

Zbiór wszystkich termów w kolekcji dokumentów nazywamy słownikiem (ang. _vocabulary), nie mylić ze słownikiem jako strukturą danych w Pythonie (dictionary).

$$V = \bigcup_{i=1}^N \{t_i^1,\dots,t_i^{|d_i|}\}$$

(To zbiór, więc liczymy bez powtórzeń!)

import Data.Set as Set hiding(map)

getVocabulary :: [Text] -> Set Text 
getVocabulary = Set.unions . map (Set.fromList . normalize) 

getVocabulary collectionD

fromList ["ala","but","chyba","kot","mie\263","podobn","ty","zgubi\263"]

Jak wyszukiwarka może być szybka?

_Odwrócony indeks (ang. inverted index) pozwala wyszukiwarce szybko szukać w milionach dokumentów. Odwrócony indeks to prostu... indeks, jaki znamy z książek (mapowanie słów na numery stron/dokumentów).

collectionDNormalized = map normalize collectionD

documentToPostings :: ([Text], Int) -> Set (Text, Int)
documentToPostings (d, ix) = Set.fromList $ map (\t -> (t, ix)) d

documentToPostings (collectionDNormalized !! 2, 2)

Use tuple-section

Found:

\ t -> (t, ix)

Why Not:

(, ix)

fromList [("chyba",2),("kot",2),("mie\263",2),("ty",2)]

collectionToPostings :: [[Text]] -> Set (Text, Int)
collectionToPostings coll = Set.unions $ map documentToPostings $ Prelude.zip coll [0..]

collectionToPostings collectionDNormalized

Use zipWith

Found:

map documentToPostings $ Prelude.zip coll [0 .. ]

Why Not:

zipWith (curry documentToPostings) coll [0 .. ]

fromList [("ala",0),("but",1),("but",3),("chyba",2),("chyba",3),("kot",0),("kot",1),("kot",2),("kot",4),("mie\263",0),("mie\263",2),("mie\263",4),("podobn",1),("ty",2),("zgubi\263",3)]

updateInvertedIndex :: (Text, Int) -> Map Text [Int] -> Map Text [Int]
updateInvertedIndex (t, ix) invIndex = insertWith (++) t [ix] invIndex

getInvertedIndex :: [[Text]] -> Map Text [Int]
getInvertedIndex = Prelude.foldr updateInvertedIndex Map.empty . Set.toList . collectionToPostings

ind = getInvertedIndex collectionDNormalized
ind
ind ! "kot"

Eta reduce

Found:

updateInvertedIndex (t, ix) invIndex
  = insertWith (++) t [ix] invIndex

Why Not:

updateInvertedIndex (t, ix) = insertWith (++) t [ix]

fromList [("ala",[0]),("but",[1,3]),("chyba",[2,3]),("kot",[0,1,2,4]),("mie\263",[0,2,4]),("podobn",[1]),("ty",[2]),("zgubi\263",[3])]

[0,1,2,4]

Relewantność

Potrafimy szybko przeszukiwać znormalizowane dokumenty, ale które dokumenty są ważne (_relewantne) względem potrzeby informacyjnej użytkownika?

Zapytania boole'owskie

pizzeria Poznań dowóz to pizzeria AND Poznań AND dowóz czy pizzeria OR Poznań OR dowóz
`(pizzeria OR pizza OR tratoria) AND Poznań AND dowóz
pizzeria AND Poznań AND dowóz AND NOT golonka

Jak domyślnie interpretować zapytanie?

jako zapytanie AND -- być może za mało dokumentów
rozwiązanie pośrednie?
jako zapytanie OR -- być może za dużo dokumentów

Możemy jakieś miary dopasowania dokumentu do zapytania, żeby móc posortować dokumenty...

Mierzenie dopasowania dokumentu do zapytania

Potrzebujemy jakieś funkcji $\sigma : Q x D \rightarrow \mathbb{R}$.

Musimy jakoś zamienić dokumenty na liczby, tj. dokumenty na wektory liczb, a całą kolekcję na macierz.

Po pierwsze ponumerujmy wszystkie termy ze słownika.

voc = getVocabulary collectionD

vocD :: Map Int Text
vocD = Map.fromList $ zip [0..] $ Set.toList voc

invvocD :: Map Text Int
invvocD = Map.fromList $ zip (Set.toList voc) [0..]

vocD

invvocD

vocD ! 0
invvocD ! "chyba"

fromList [(0,"ala"),(1,"but"),(2,"chyba"),(3,"kot"),(4,"mie\263"),(5,"podobn"),(6,"ty"),(7,"zgubi\263")]

fromList [("ala",0),("but",1),("chyba",2),("kot",3),("mie\263",4),("podobn",5),("ty",6),("zgubi\263",7)]

ala

Napiszmy funkcję, która _wektoryzuje znormalizowany dokument.

vectorize :: Int -> Map Int Text -> [Text] -> [Double]
vectorize vecSize v doc = map (\i -> count (v ! i) doc) $ [0..(vecSize-1)]
   where count t doc 
           | t `elem` doc = 1.0
           | otherwise = 0.0
           
vocSize = Set.size voc

(collectionDNormalized !! 2)
vectorize vocSize vocD (collectionDNormalized !! 2)

Redundant $

Found:

map (\ i -> count (v ! i) doc) $ [0 .. (vecSize - 1)]

Why Not:

map (\ i -> count (v ! i) doc) [0 .. (vecSize - 1)]

Redundant bracket

Found:

(collectionDNormalized !! 2)

Why Not:

collectionDNormalized !! 2

ty

chyba

mieć

kot

[0.0,0.0,1.0,1.0,1.0,0.0,1.0,0.0]

Jak inaczej uwzględnić częstość wyrazów?

$ \newcommand{\idf}{\mathop{\rm idf}\nolimits} \newcommand{\tf}{\mathop{\rm tf}\nolimits} \newcommand{\df}{\mathop{\rm df}\nolimits} \newcommand{\tfidf}{\mathop{\rm tfidf}\nolimits} $

$\tf_{t,d}$ - term frequency
$1+\log(\tf_{t,d})$
$0.5 + \frac{0.5 \times \tf_{t,d}}{max_t(\tf_{t,d})}$

vectorizeTf :: Int -> Map Int Text -> [Text] -> [Double]
vectorizeTf vecSize v doc = map (\i -> count (v ! i) doc) $ [0..(vecSize-1)]
   where count t doc = fromIntegral $ (Prelude.length . Prelude.filter (== t)) doc

vocSize = Set.size voc

(collectionDNormalized !! 4)
vectorize vocSize vocD (collectionDNormalized !! 4)
vectorizeTf vocSize vocD (collectionDNormalized !! 4)

Redundant $

Found:

map (\ i -> count (v ! i) doc) $ [0 .. (vecSize - 1)]

Why Not:

map (\ i -> count (v ! i) doc) [0 .. (vecSize - 1)]

Redundant bracket

Found:

(collectionDNormalized !! 4)

Why Not:

collectionDNormalized !! 4

kot

mieć

kot

[0.0,0.0,0.0,1.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,2.0,1.0,0.0,0.0,0.0]

$ \newcommand{\idf}{\mathop{\rm idf}\nolimits} \newcommand{\tf}{\mathop{\rm tf}\nolimits} \newcommand{\df}{\mathop{\rm df}\nolimits} \newcommand{\tfidf}{\mathop{\rm tfidf}\nolimits} $

Odwrotna częstość dokumentowa

Czy wszystkie wyrazy są tak samo ważne?

NIE. Wyrazy pojawiające się w wielu dokumentach są mniej ważne.

Aby to uwzględnić, przemnażamy frekwencję wyrazu przez _odwrotną częstość w dokumentachinverse document frequency):

$$\idf_t = \log \frac{N}{\df_t},$$

gdzie:

$\idf_t$ - odwrotna częstość wyrazu $t$ w dokumentach
$N$ - liczba dokumentów w kolekcji
$\df_f$ - w ilu dokumentach wystąpił wyraz $t$?

Dlaczego idf?

term $t$ wystąpił...

w 1 dokumencie, $\idf_t = \log N/1 = \log N$
2 razy w kolekcji, $\idf_t = \log N/2$ lub $\log N$
w połowie dokumentów kolekcji, $\idf_t = \log N/(N/2) = \log 2$
we wszystkich dokumentach, $\idf_t = \log N/N = \log 1 = 0$

idf :: [[Text]] -> Text -> Double
idf coll t = log (fromIntegral n / fromIntegral df)
  where df = Prelude.length $ Prelude.filter (\d -> t `elem` d) coll
        n = Prelude.length coll
        
idf collectionDNormalized "kot"

0.22314355131420976

idf collectionDNormalized "chyba"

0.9162907318741551

Co z tego wynika?

Zamiast $\tf_{t,d}$ będziemy w wektorach rozpatrywać wartości:

$$\tfidf_{t,d} = \tf_{t,d} \times \idf_{t}$$

vectorizeTfIdf :: Int -> [[Text]] -> Map Int Text -> [Text] -> [Double]
vectorizeTfIdf vecSize coll v doc = map (\i -> count (v ! i) doc * idf coll (v ! i)) [0..(vecSize-1)]
   where count t doc = fromIntegral $ (Prelude.length . Prelude.filter (== t)) doc

vocSize = Set.size voc

collectionDNormalized !! 4
vectorize vocSize vocD (collectionDNormalized !! 4)
vectorizeTf vocSize vocD (collectionDNormalized !! 4)
vectorizeTfIdf vocSize collectionDNormalized vocD (collectionDNormalized !! 4)

kot

mieć

kot

[0.0,0.0,0.0,1.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,2.0,1.0,0.0,0.0,0.0]

[0.0,0.0,0.0,0.44628710262841953,0.5108256237659907,0.0,0.0,0.0]

map (vectorizeTfIdf vocSize collectionDNormalized vocD) collectionDNormalized

[[1.6094379124341003,0.0,0.0,0.22314355131420976,0.5108256237659907,0.0,0.0,0.0],[0.0,0.9162907318741551,0.0,0.22314355131420976,0.0,1.6094379124341003,0.0,0.0],[0.0,0.0,0.9162907318741551,0.22314355131420976,0.5108256237659907,0.0,1.6094379124341003,0.0],[0.0,0.9162907318741551,0.9162907318741551,0.0,0.0,0.0,0.0,1.6094379124341003],[0.0,0.0,0.0,0.44628710262841953,0.5108256237659907,0.0,0.0,0.0]]

Teraz zdefiniujemy _overlap score measure:

$$\sigma(q,d) = \sum_{t \in q} \tfidf_{t,d}$$

Podobieństwo kosinusowe

_Overlap score measure nie jest jedyną możliwą metryką, za pomocą której możemy mierzyć dopasowanie dokumentu do zapytania. Możemy również sięgnąć po intuicje geometryczne (skoro mamy do czynienia z wektorami).

Pytanie: Ile wymiarów mają wektory, na których operujemy? Jak "wyglądają" te wektory? Czy możemy wykonywać na nich standardowe operacje geometryczne czy te, które znamy z geometrii liniowej?

Podobieństwo między dokumentami

Zajmijmy się teraz poszukiwaniem miary mierzącej podobieństwo między dokumentami $d_1$ i $d_2$ (czyli poszukujemy sensownej funkcji $\sigma : D x D \rightarrow \mathbb{R}$).

Uwaga Pojęcia "miary" używamy nieformalnie, nie spełnia ona założeń znanych z teorii miary.

Rozpatrzmy zbiorek tekstów legend miejskich z git://gonito.net/polish-urban-legends.

(To autentyczne teksty z Internentu, z językiem potocznym, wulgarnym itd.)

   git clone git://gonito.net/polish-urban-legends
   paste polish-urban-legends/dev-0/expected.tsv polish-urban-legends/dev-0/in.tsv > legendy.txt

import System.IO
import Data.List.Split as SP

legendsh <- openFile "legendy.txt" ReadMode
hSetEncoding legendsh utf8
contents <- hGetContents legendsh
ls = Prelude.lines contents
items = map (map pack . SP.splitOn "\t") ls
Prelude.head items

na_ak

Opowieść prawdziwa... Olsztyn, akademik, 7 piętro, […]

nbOfLegends = Prelude.length items
nbOfLegends

labelsL = map Prelude.head items
labelsL
collectionL = map (!!1) items
items !! 1

na_ak

w_lud

ba_hy

w_lap

ne_dz

be_wy

zw_oz

mo_zu

be_wy

ba_hy

mo_zu

be_wy

w_lud

ne_dz

ta_ab

ta_ab

ta_ab

w_lap

ba_hy

ne_dz

ba_hy

tr_su

ne_dz

ba_hy

mo_zu

tr_su

zw_oz

ne_dz

ne_dz

w_lud

zw_oz

zw_oz

zw_oz

ne_dz

ta_ab

zw_oz

w_lud

na_ak

zw_oz

w_lap

be_wy

na_ak

zw_oz

w_lap

na_ak

ba_hy

zw_oz

w_lud

zw_oz

zw_oz

mo_zu

ba_hy

zw_oz

tr_su

na_ak

ba_hy

w_lud

w_lud

zw_oz

tr_su

zw_oz

w_lud

zw_oz

zw_oz

be_wy

tr_su

zw_oz

na_ak

ba_hy

zw_oz

ne_dz

ba_hy

na_ak

zw_oz

w_lud

mo_zu

mo_zu

na_ak

w_lap

ne_dz

ba_hy

mo_zu

ba_hy

ne_dz

zw_oz

tr_su

ne_dz

w_lud

Ja podejrzewam że o polowaniu nie było mowy, po prostu znalazł martwego szczupaka i skorzystał z okazji! Mnie mocno zdziwiła jego siła żeby taki pół kilogramowy okaz szczupaka przesuwać o parę metrów i to w trzcinach! Szacuneczek. Przypomniala mi sie historia którą kiedys zaslyszalem o wlascicielce pytona, ktory nagle polozyl sie wzdluz jej łóżka. Leżał tak wyciągniety jak struna dłuższy czas jak nieżywy (a był długości łóżka), więc kobitka zadzonila do weterynarza co ma robić. Usłyszała że ma szybko zamknąć się w łazience i poczekać na niego bo pyton ją mierzy jako potencjalną ofiarę (czy mu się zmieści w brzuchu...). Wierzyć, nie wierzyć? Kiedyś nie wierzyłem ale od kilku dni mam wątpliwosci... Pozdrawiam

collectionLNormalized = map normalize collectionL
voc' = getVocabulary collectionL

vocLSize = Prelude.length voc'

vocL :: Map Int Text
vocL = Map.fromList $ zip [0..] $ Set.toList voc'

invvocL :: Map Text Int
invvocL = Map.fromList $ zip (Set.toList voc') [0..]

vocL ! 0
invvocL ! "chyba"

Wektoryzujemy całą kolekcję:

lVectorized = map (vectorizeTfIdf vocLSize collectionLNormalized vocL) collectionLNormalized
lVectorized !! 1

[0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.38837067474886433,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.752336051950276,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0647107369924282,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2078115806331018,0.0,0.0,0.0,0.0,0.0,1.247032293786383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.5947071077466928,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.268683541318364,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2078115806331018,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.7578579175523736,0.0,0.0,0.0,0.0,0.0,0.3550342544812725,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.9395475940384223,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.21437689194643514,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2878542883066382,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.2745334443309775,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,1.247032293786383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.386466576974748,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,1.0319209141694374,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,2.340142505300509,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.7578579175523736,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.5214691394881432,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,8.388148398070203e-2,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.9810014688665833,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.6096847248398047,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.575536360758419,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.1847155011136463,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0319209141694374,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.322773392263051,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.900958761193047,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,3.079613757534693,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.340142505300509,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.710068508962545,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,8.931816237309167,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.5199979695992702,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0319209141694374,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.26121549926361765,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.6741486494265287,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.386466576974748,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,9.238841272604079,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.330413902725434,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.163323025660538,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.367295829986474,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.12210269680089991,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.7727609380946383,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.465908118654584,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.068012845856213,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.856470206220483,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,3.079613757534693,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,5.712940412440966,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,2.068012845856213,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]

Szukamy funkcji $sigma$, która da wysoką wartość dla tekstów dotyczących tego samego wątku legendowego (np. $d_1$ i $d_2$ mówią o wężu przymierzającym się do zjedzenia swojej właścicielki) i niską dla tekstów z różnych wątków (np. $d_1$ opowiada o wężu ludojadzie, $d_2$ - bałwanku na hydrancie).

Może po prostu odległość euklidesowa, skoro to punkty w wielowymiarowej przestrzeni?

import Text.Printf
import Data.List (take)

formatNumber :: Double -> String
formatNumber x = printf "% 7.2f" x

similarTo :: ([Double] -> [Double] -> Double) -> [[Double]] -> Int -> Text
similarTo simFun vs ix = pack $ Prelude.unwords $ map (formatNumber . ((vs !! ix) `simFun`)) vs

euclDistance :: [Double] -> [Double] -> Double
euclDistance v1 v2 = sqrt $ sum $ Prelude.zipWith (\x1 x2 -> (x1 - x2)**2) v1 v2

limit = 13
labelsLimited =  Data.List.take limit labelsL
limitedL = Data.List.take limit lVectorized

similarTo euclDistance limitedL 0

Eta reduce

Found:

formatNumber x = printf "% 7.2f" x

Why Not:

formatNumber = printf "% 7.2f"

   0.00   79.93   78.37   76.57   87.95   81.15   82.77  127.50  124.54   76.42   84.19   78.90   90.90

paintMatrix :: ([Double] -> [Double] -> Double) -> [Text] -> [[Double]] -> Text
paintMatrix simFun labels vs = header <> "\n" <> (Data.Text.unlines $ map (\(lab, ix) -> lab <> " " <> similarTo simFun vs ix) $ zip labels [0..(Prelude.length vs - 1)])
    where header = "      " <> (Data.Text.unwords $ map (\l -> pack $ printf "% 7s" l) labels)
    
paintMatrix euclDistance labelsLimited limitedL

Move brackets to avoid $

Found:

"\n"
  <>
    (Data.Text.unlines
       $ map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
           $ zip labels [0 .. (Prelude.length vs - 1)])

Why Not:

"\n"
  <>
    Data.Text.unlines
      (map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
         $ zip labels [0 .. (Prelude.length vs - 1)])

Use zipWith

Found:

map (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix)
  $ zip labels [0 .. (Prelude.length vs - 1)]

Why Not:

zipWith
  (curry (\ (lab, ix) -> lab <> " " <> similarTo simFun vs ix))
  labels [0 .. (Prelude.length vs - 1)]

Move brackets to avoid $

Found:

"      "
  <> (Data.Text.unwords $ map (\ l -> pack $ printf "% 7s" l) labels)

Why Not:

"      "
  <> Data.Text.unwords (map (\ l -> pack $ printf "% 7s" l) labels)

Avoid lambda

Found:

\ l -> pack $ printf "% 7s" l

Why Not:

pack . printf "% 7s"

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak    0.00   79.93   78.37   76.57   87.95   81.15   82.77  127.50  124.54   76.42   84.19   78.90   90.90
w_lud   79.93    0.00   38.92   34.35   56.48   44.89   47.21  109.24  104.82   35.33   49.88   39.98   60.20
ba_hy   78.37   38.92    0.00   30.37   54.23   40.93   43.83  108.15  102.91   27.37   46.95   35.81   58.99
w_lap   76.57   34.35   30.37    0.00   51.54   37.46   40.86  107.43  103.22   25.22   43.66   32.10   56.53
ne_dz   87.95   56.48   54.23   51.54    0.00   57.98   60.32  113.66  109.59   50.96   62.17   54.84   70.70
be_wy   81.15   44.89   40.93   37.46   57.98    0.00   49.55  110.37  100.50   37.77   51.54   37.09   62.92
zw_oz   82.77   47.21   43.83   40.86   60.32   49.55    0.00  111.11  107.57   41.02   54.07   45.23   64.65
mo_zu  127.50  109.24  108.15  107.43  113.66  110.37  111.11    0.00  139.57  107.38  109.91  108.20  117.07
be_wy  124.54  104.82  102.91  103.22  109.59  100.50  107.57  139.57    0.00  102.69  108.32   99.06  113.25
ba_hy   76.42   35.33   27.37   25.22   50.96   37.77   41.02  107.38  102.69    0.00   43.83   32.08   56.68
mo_zu   84.19   49.88   46.95   43.66   62.17   51.54   54.07  109.91  108.32   43.83    0.00   47.87   66.40
be_wy   78.90   39.98   35.81   32.10   54.84   37.09   45.23  108.20   99.06   32.08   47.87    0.00   59.66
w_lud   90.90   60.20   58.99   56.53   70.70   62.92   64.65  117.07  113.25   56.68   66.40   59.66    0.00

Problem: za dużo zależy od długości tekstu.

Rozwiązanie: znormalizować wektor $v$ do wektora jednostkowego.

$$ \vec{1}(v) = \frac{v}{|v|} $$

Taki wektor ma długość 1!

vectorNorm :: [Double] -> Double
vectorNorm vs = sqrt $ sum $ map (\x -> x * x) vs

toUnitVector :: [Double] -> [Double]
toUnitVector vs = map (/ n) vs
   where n = vectorNorm vs

vectorNorm (toUnitVector [3.0, 4.0])

euclDistanceNormalized :: [Double] -> [Double] -> Double
euclDistanceNormalized v1 v2 = toUnitVector v1 `euclDistance` toUnitVector v2

euclSim v1 v2 = 1 / (d + 0.1)
   where d = euclDistanceNormalized v1 v2

paintMatrix euclSim labelsLimited limitedL

1.0

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak   10.00    0.67    0.66    0.66    0.67    0.67    0.67    0.67    0.67    0.67    0.66    0.67    0.67
w_lud    0.67   10.00    0.67    0.68    0.67    0.66    0.67    0.67    0.68    0.66    0.67    0.67    0.68
ba_hy    0.66    0.67   10.00    0.66    0.67    0.67    0.67    0.67    0.69    0.74    0.66    0.67    0.66
w_lap    0.66    0.68    0.66   10.00    0.66    0.66    0.66    0.66    0.67    0.66    0.66    0.66    0.66
ne_dz    0.67    0.67    0.67    0.66   10.00    0.67    0.67    0.68    0.69    0.68    0.67    0.67    0.68
be_wy    0.67    0.66    0.67    0.66    0.67   10.00    0.66    0.67    0.74    0.66    0.67    0.76    0.66
zw_oz    0.67    0.67    0.67    0.66    0.67    0.66   10.00    0.67    0.67    0.66    0.66    0.67    0.67
mo_zu    0.67    0.67    0.67    0.66    0.68    0.67    0.67   10.00    0.69    0.67    0.69    0.68    0.67
be_wy    0.67    0.68    0.69    0.67    0.69    0.74    0.67    0.69   10.00    0.68    0.67    0.75    0.67
ba_hy    0.67    0.66    0.74    0.66    0.68    0.66    0.66    0.67    0.68   10.00    0.66    0.67    0.66
mo_zu    0.66    0.67    0.66    0.66    0.67    0.67    0.66    0.69    0.67    0.66   10.00    0.67    0.67
be_wy    0.67    0.67    0.67    0.66    0.67    0.76    0.67    0.68    0.75    0.67    0.67   10.00    0.67
w_lud    0.67    0.68    0.66    0.66    0.68    0.66    0.67    0.67    0.67    0.66    0.67    0.67   10.00

Podobieństwo kosinusowe

Częściej zamiast odległości euklidesowej stosuje się podobieństwo kosinusowe, czyli kosinus kąta między wektorami.

Wektor dokumentu ($\vec{V}(d)$) - wektor, którego składowe odpowiadają wyrazom.

$$\sigma(d_1,d_2) = \cos\theta(\vec{V}(d_1),\vec{V}(d_2)) = \frac{\vec{V}(d_1) \cdot \vec{V}(d_2)}{|\vec{V}(d_1)||\vec{V}(d_2)|} $$

Zauważmy, że jest to iloczyn skalarny znormalizowanych wektorów!

$$\sigma(d_1,d_2) = \vec{1}(\vec{V}(d_1)) \times \vec{1}(\vec{V}(d_2)) $$

(✕) :: [Double] -> [Double] -> Double
(✕) v1 v2 = sum $ Prelude.zipWith (*) v1 v2

[2, 1, 0] ✕ [-2, 5, 10]

1.0

cosineSim v1 v2 = toUnitVector v1 ✕ toUnitVector v2

paintMatrix cosineSim labelsLimited limitedL

        na_ak   w_lud   ba_hy   w_lap   ne_dz   be_wy   zw_oz   mo_zu   be_wy   ba_hy   mo_zu   be_wy   w_lud
na_ak    1.00    0.02    0.01    0.01    0.03    0.02    0.02    0.04    0.03    0.02    0.01    0.02    0.03
w_lud    0.02    1.00    0.02    0.05    0.04    0.01    0.03    0.04    0.06    0.01    0.02    0.03    0.06
ba_hy    0.01    0.02    1.00    0.01    0.02    0.03    0.03    0.04    0.08    0.22    0.01    0.04    0.01
w_lap    0.01    0.05    0.01    1.00    0.01    0.01    0.00    0.01    0.02    0.00    0.00    0.00    0.00
ne_dz    0.03    0.04    0.02    0.01    1.00    0.04    0.03    0.07    0.08    0.06    0.03    0.03    0.05
be_wy    0.02    0.01    0.03    0.01    0.04    1.00    0.01    0.03    0.21    0.01    0.02    0.25    0.01
zw_oz    0.02    0.03    0.03    0.00    0.03    0.01    1.00    0.04    0.03    0.00    0.01    0.02    0.02
mo_zu    0.04    0.04    0.04    0.01    0.07    0.03    0.04    1.00    0.10    0.02    0.09    0.05    0.04
be_wy    0.03    0.06    0.08    0.02    0.08    0.21    0.03    0.10    1.00    0.05    0.03    0.24    0.04
ba_hy    0.02    0.01    0.22    0.00    0.06    0.01    0.00    0.02    0.05    1.00    0.01    0.02    0.00
mo_zu    0.01    0.02    0.01    0.00    0.03    0.02    0.01    0.09    0.03    0.01    1.00    0.01    0.02
be_wy    0.02    0.03    0.04    0.00    0.03    0.25    0.02    0.05    0.24    0.02    0.01    1.00    0.02
w_lud    0.03    0.06    0.01    0.00    0.05    0.01    0.02    0.04    0.04    0.00    0.02    0.02    1.00

collectionL !! 5

na tylnym siedzeniu w autobusie siedzi matka z 7-8 letnim synkiem. […]

collectionL !! 8

Krótko zwięźle i na temat. Zastanawia mnie jak ludzie wychowują dzieci. […]

Z powrotem do wyszukiwarek

Możemy potraktować zapytanie jako bardzo krótki dokument, dokonać jego wektoryzacji i policzyć cosinus kąta między zapytaniem a dokumentem.

import Data.Ord
import Data.List

legendVectorizer = vectorizeTfIdf vocLSize collectionLNormalized vocL . normalize


query vs vzer q = map ((collectionL !!) . snd) $ Data.List.take 3 $ sortBy (\a b -> fst b `compare` fst a) $ zip (map (`cosineSim` qvec) vs) [0..]  
   where qvec = vzer q 

query lVectorized legendVectorizer "wąż przymierza się do zjedzenia właścicielki"

ja za to znam przypadek, że koleżanka mieszkala w bloku parę lat temu, pewnego razu wchodzi do łazienki w samej bieliźnie a tam ogromny wąż na podłodze i tak się wystraszyła że wybiegła z wrzaskiem z mieszkania i wyleciała przed blok w samej bieliźnie i uciekła do babci swojej, która mieszkala gdzieś niedaleko. a potem się okazało, że jej sąsiad z dołu hodował sobie węża i tak właśnie swobodnie go "pasał" po mieszkaniu i wąż mu spierdzielił przez rurę w łazience :cool :

Pewna dziewczyna, wieku mi nieznanego, w mieście stołecznym - rozwiodła się. Była sama i samotna, więc zapragnęła kupić sobie zwierzę, […]

Anakonda. Czy to kolejna miejska legenda? Jakiś czas temu koleżanka na jednej z imprez towarzyskich opowiedziała mrożącą krew w żyłach historię o dziewczynie ze swojej pracy, która w Warszawie na dyskotece w Dekadzie poznała chłopaka. […]

192 KiB Raw Blame History Unescape Escape

Ekstrakcja informacji

3. Wyszukiwarki — TF-IDF [wykład]

Filip Graliński (2021)

Wyszukiwarka - szybka i sensowna

Roboczy przykład

Wydobycie tekstu

Normalizacja tekstu

Tokenizacja

Problemy z tokenizacją

Język angielski

Inne języki?

Lematyzacja

Stemowanie

_Stop words

Normalizacja - różności

Normalizacja jako całościowy proces

Jak wyszukiwarka może być szybka?

Relewantność

Zapytania boole'owskie

Mierzenie dopasowania dokumentu do zapytania

Jak inaczej uwzględnić częstość wyrazów?

Odwrotna częstość dokumentowa

Dlaczego idf?

Co z tego wynika?

Podobieństwo kosinusowe

Podobieństwo między dokumentami

Podobieństwo kosinusowe

Z powrotem do wyszukiwarek

192 KiB

Raw Blame History