aitech-eks-pub/wyk/11_rnn.ipynb

Rekurencyjne sieci neuronowe

Inne spojrzenie na sieci przedstawione do tej pory

Regresja liniowa/logistyczna lub klasyfikacja wieloklasowa na całym tekście

W regresji liniowej czy logistycznej bądź w klasyfikacji wieloklasowej (z funkcją Softmax) stosowaliśmy następujący schemat:

Do tej pory patrzyliśmy na to tak, że po prostu cały tekst jest od razu przetwarzany przez (prostą) sieć neuronową, popatrzmy na ten przypadek, jak na sytuację przetwarzania sekwencyjnego. Będzie to trochę sztuczne, ale uogólnimy to potem w sensowny sposób.

Wektoryzacja

Po pierwsze, zauważmy, że w wielu schematach wektoryzacji (np. tf), wektor dokumentów jest po prostu sumą wektorów poszczególnych składowych:

$$\vec{v}(d) = \vec{v}(t^1,\ldots,t^K) = \vec{v}(t^1) + \ldots + \vec{v}(t^K) = \sum_{k=1}^K \vec{v}(t^i),$$

gdzie w schemacie tf \vec{v}(tⁱ) to po prostu wektor _one-hot dla słowa.

Pytanie Jak postać przyjmie w \vec{v}(tⁱ) dla wektoryzacji tf-idf?

Wektory $\vec{v}(t^k)$ mogą być również gęstymi wektorami ($\vec{v}(t^k) \in \mathcal{R}^n$, gdzie $n$ jest rzędu 10-1000), np. w modelu Word2vec albo mogą to być wyuczalne wektory (zanurzenia słów, _embeddings), tzn. wektory, które są parametrami uczonej sieci!

Pytanie Ile wag (parametrów) wnoszą wyuczalne wektory do sieci?

Prosta wektoryzacja wyrażona w modelu sekwencyjnym

Jak zapisać równoważnie powyższą wektoryzację w modelu sekwencyjnym, tj. przy założeniu, że przetwarzamy wejście token po tokenie (a nie „naraz”)? Ogólnie wprowadzimy bardzo ogólny model sieci rekurencyjnej.

Po pierwsze zakładamy, że sieć ma pewien stan $\vec{s^k} \in \mathcal{R}^m$ (stan jest wektorem o długości $m$), który może zmieniać się z każdym krokiem (przetwarzanym tokenem). Zmiana stanu jest określona przez pewną funkcję $R : \mathcal{R}^m \times \mathcal{R}^n \rightarrow \mathcal{R}^m$ ($n$ to rozmiar wektorów $\vec{v}(t^k)$):

$$\vec{s^k} = R(\vec{s^{k-1}}, \vec{v}(t^k)).$$

W przypadku wektoryzacji tf-idf mamy do czynienia z prostym sumowaniem, więc $R$ przyjmuje bardzo prostą postać:

$$\vec{s^0} = [0,\dots,0],$$

$$R(\vec{s}, \vec{x}) = \vec{s} + \vec{x}.$$

Wyjście z modelu

Dla regresji liniowej/logistycznej, oprócz funkcji $R$, która określa zmianę stanu, potrzebujemy funkcji $O$, która określa wyjście systemu w każdym kroku.

$$y^k = O(\vec{s^k})$$

W zadaniach klasyfikacji czy regresji, kiedy patrzymy na cały tekst w zasadzie wystarczy wziąć _ostatnią wartość (tj. $y^K$). Można sobie wyobrazić sytuację, kiedy wartości $y^k$ dla $k < k$ również mogą być jakoś przydatne (np. klasyfikujemy na bieżąco tekst wpisywany przez użytkownika).

W każdym razie dla regresji liniowej funkcja $O$ przyjmie postać:

$$O(\vec{s}) = \vec{w}\vec{s}$$,

gdzie $\vec{w}$ jest wektorem wyuczylnych wag, dla regresji zaś logistycznej:

$$O(\vec{s}) = \operatorname{softmax}(\vec{w}\vec{s})$$

Pytanie: jaką postać przyjmie $O$ dla klasyfikacji wieloklasowej

Prosta sieć rekurencyjna

W najprostszej sieci rekurencyjnej (_Vanilla RNN, sieć Elmana, czasami po prostu RNN) w każdym kroku oprócz właściwego wejścia ($\vec{v}(t^k)$) będziemy również podawać na wejściu poprzedni stan sieci ($\vec{s^{k-1}}$).

Innymi słowy, funkcje $R$ przyjmie następującą postać:

$$s^k = \sigma(W\langle\vec{v}(t^k), \vec{s^{k-1}}\rangle + \vec{b}),$$

gdzie:

• $\langle\vec{x},\vec{y}\rangle$ to konkatenacja dwóch wektorów,
• $W \in \mathcal{R}^m \times \mathcal{R}^{n+m}$ — macierz wag,
• $b \in \mathcal{R}^m$ — wektor obciążeń (_biases).

Taką sieć RNN można przedstawić schematycznie w następujący sposób:

Zauważmy, że zamiast macierzy $W$ działającej na konkatenacji wektorów można wprowadzić dwie macierze $U$ i $V$ i tak zapisać wzór:

$$s^k = \sigma(U\vec{v}(t^k) + V\vec{s^{k-1}} + \vec{b}).$$

Jeszcze inne spojrzenie na sieć RNN:

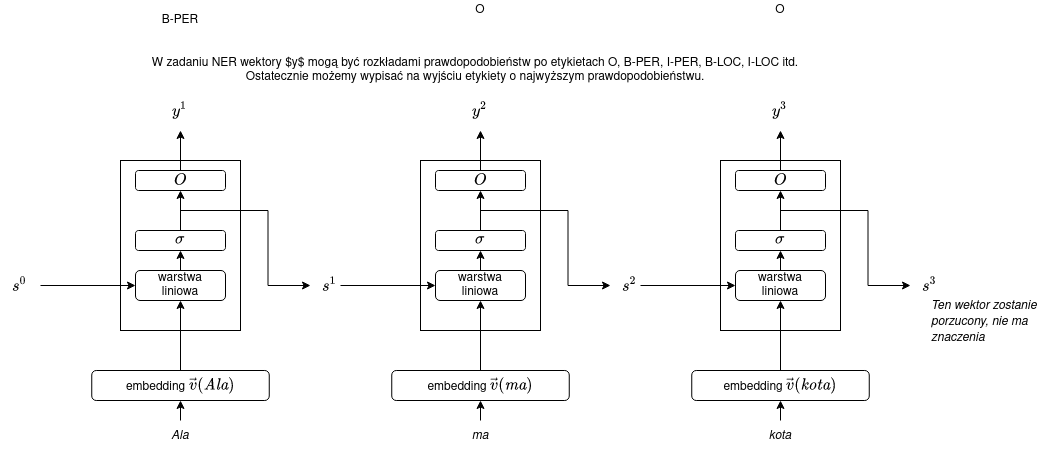
Powyższy rysunek przedstawia pojedynczy krok sieci RNN. Dla całego wejścia (powiedzmy, 3-wyrazowego) możemy sieć rozwinąć (_unroll):

Zastosowanie sieci RNN do etykietowania sekwencji

Problemy z prostymi sieciami RNN

W praktyce proste sieci RNN są bardzo trudne w uczenia, zazwyczaj pojawia się problem zanikających (rzadziej: eksplodujących) gradientów: w propagacji wstecznej błąd szybko zanika i nie jest w stanie dotrzeć do początkowych wejść.

Sieci RNN z bramkami

W prostych sieciach RNN podstawowa trudność polega na tym, że mamy niewielką kontrolę nad tym jak pamięć (stan) jest aktualizowana. Aby zwiększyć tę kontrolę, potrzebujemy bramek.

Bramki

Zazwyczaj do tej pory rozpatrywaliśmy iloczyn skalarny wektorów, w wyniku którego otrzymujemy liczbę (w PyTorchu wyrażany za pomocą operatora @), np.

import torch

a = torch.tensor([-1, 0, 3])
b = torch.tensor([2, 5, -1])
a @ b

# Out[2]:
tensor(-5)

Czasami przydatny jest iloczyn Hadamarda, czyli przemnożenie wektorów (albo macierzy) po współrzędnych. W PyTorchu taki iloczyn wyrażany jest za pomocą operatora *, w notacji matematycznej będziemy używali znaku $\odot$.

import torch

a = torch.tensor([-1, 0, 3])
b = torch.tensor([2, 5, -1])
a * b

# Out[3]:
tensor([-2,  0, -3])

Zauważmy, że iloczyn Hadamarda przez wektor złożony z zer i jedynek daje nam _filtr, możemy selektywnie wygaszać pozycje wektora, np. tutaj wyzerowaliśmy 2. i 5. pozycję wektora:

import torch

a = torch.tensor([1., 2., 3., 4., 5.])
b = torch.tensor([1., 0., 1., 1., 0.])
a * b

# Out[4]:
tensor([1., 0., 3., 4., 0.])

Co więcej, za pomocą bramki możemy selektywnie kontrolować, co zapamiętujemy, a co zapominamy. Rozpatrzmy mianowicie wektor zer i jedynek $\vec{g} \in \{0,1\}^m$, dla stanu (pamięci) $\vec{s}$ i nowej informacji $\vec{x}$ możemy dokonywać aktualizacji w następujący sposób:

$$\vec{s} \leftarrow \vec{g} \odot \vec{x} + (1 - \vec{g}) \odot \vec{s}$$

Na przykład, za pomocą bramki można wpisać nową wartość na 2. i 5. pozycję wektora.

import torch

s = torch.tensor([1., 2., 3., 4., 5.])
x = torch.tensor([8., 7., 15., -3., -8.])

g = torch.tensor([0., 1., 0., 0., 1.])

s = g * x + (1 - g) * s
s

# Out[8]:
tensor([ 1.,  7.,  3.,  4., -8.])

Wektor bramki nie musi być z góry określony, może być wyuczalny. Wtedy jednak lepiej założyć, że bramka jest „miękka”, np. jej wartości pochodzi z sigmoidy zastosowanej do jakiejś wcześniejszej warstwy.

import torch

s = torch.tensor([1., 2., 3., 4., 5.])
x = torch.tensor([8., 7., 15., -3., -8.])

pre_g = torch.tensor([-2.5, 10.0, -1.2, -101., 1.3])
g = torch.sigmoid(pre_g)

s = g * x + (1 - g) * s
s

# Out[14]:
tensor([ 1.5310,  6.9998,  5.7777,  4.0000, -5.2159])

Pytanie: dlaczego sigmoida zamiast tanh?

Sieć LSTM

Architektura LSTM (_Long Short-Term Memory) pozwala rozwiązać problem znikających gradientów — za cenę komplikacji obliczeń.

W sieci LSTM stan $\vec{s^k}$ ma dwie połówki, tj. $\vec{s^k} = \langle\vec{c^k},\vec{h^k}\rangle$, gdzie

• $\vec{c^k}$ to komórka pamięci, która nie zmienia swojej, chyba że celowo zmodyfikujemy jej wartość za pomocą bramek,
• $\vec{h^k}$ to ukryty stan (przypominający $\vec{s^k}$ ze zwykłej sieci RNN).

Sieć LSTM zawiera 3 bramki:

• bramkę zapominania (_forget gate), która steruje wymazywaniem informacji z komórki pamięci $\vec{c^k}$,
• bramkę wejścia (_input gate), która steruje tym, na ile nowe informacje aktualizują komórkę pamięci $\vec{c^k}$,
• bramkę wyjścia (_output gate), która steruje tym, co z komórki pamięci przekazywane jest na wyjście.

Wszystkie trzy bramki definiowane są za pomocą bardzo podobnego wzoru — warstwy liniowej na poprzedniej wartości warstwy ukrytej i bieżącego wejścia.

$$\vec{i} = \sigma(W_i\langle\vec{v}(t^k),\vec{h^{k-1}}\rangle)$$

$$\vec{f} = \sigma(W_f\langle\vec{v}(t^k),\vec{h^{k-1}}\rangle)$$

$$\vec{o} = \sigma(W_o\langle\vec{v}(t^k),\vec{h^{k-1}}\rangle)$$

Jak widać, wzory różnią się tylko macierzami wag $W_*$.

Zmiana komórki pamięci jest zdefiniowana jak następuje:

$$\vec{c^k} = \vec{f} \odot \vec{c^{k-1}} + \vec{i} \vec{z^k}$$,

gdzie

$$\vec{z^k} = \operatorname{tanh}(W_z\langle\vec{v}(t^k),\vec{h^{k-1}}\rangle)$$

Stan ukryty zmienia się w następujący sposób:

$$\vec{h^K} = \vec{o} \odot \operatorname{tanh}(\vec{c^k})$$.

Ostateczne wyjście może być wyliczane na podstawie wektora $\vec{h^k}$:

$$O(\vec{s}) = O(\langle\vec{c},\vec{h}\rangle) = \vec{h}$$

Pytanie: Ile wag/parametrów ma sieć RNN o rozmiarze wejścia $n$ i rozmiarze warstwy ukrytej $m$?

Literatura

Yoav Goldberg, _Neural Network Methods for Natural Language Processing, Morgan & Claypool Publishers, 2017