5.8 KiB
Regresja liniowa
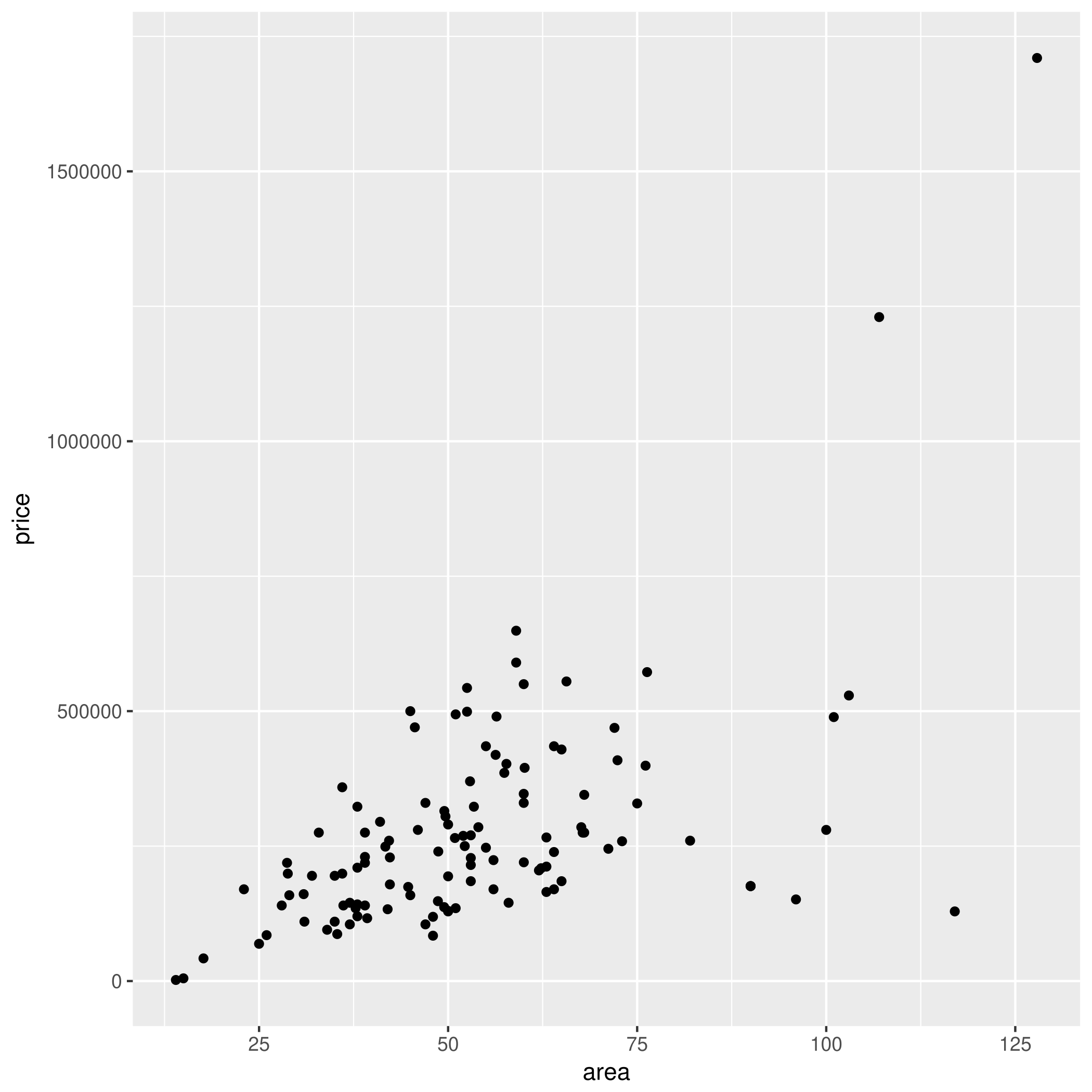
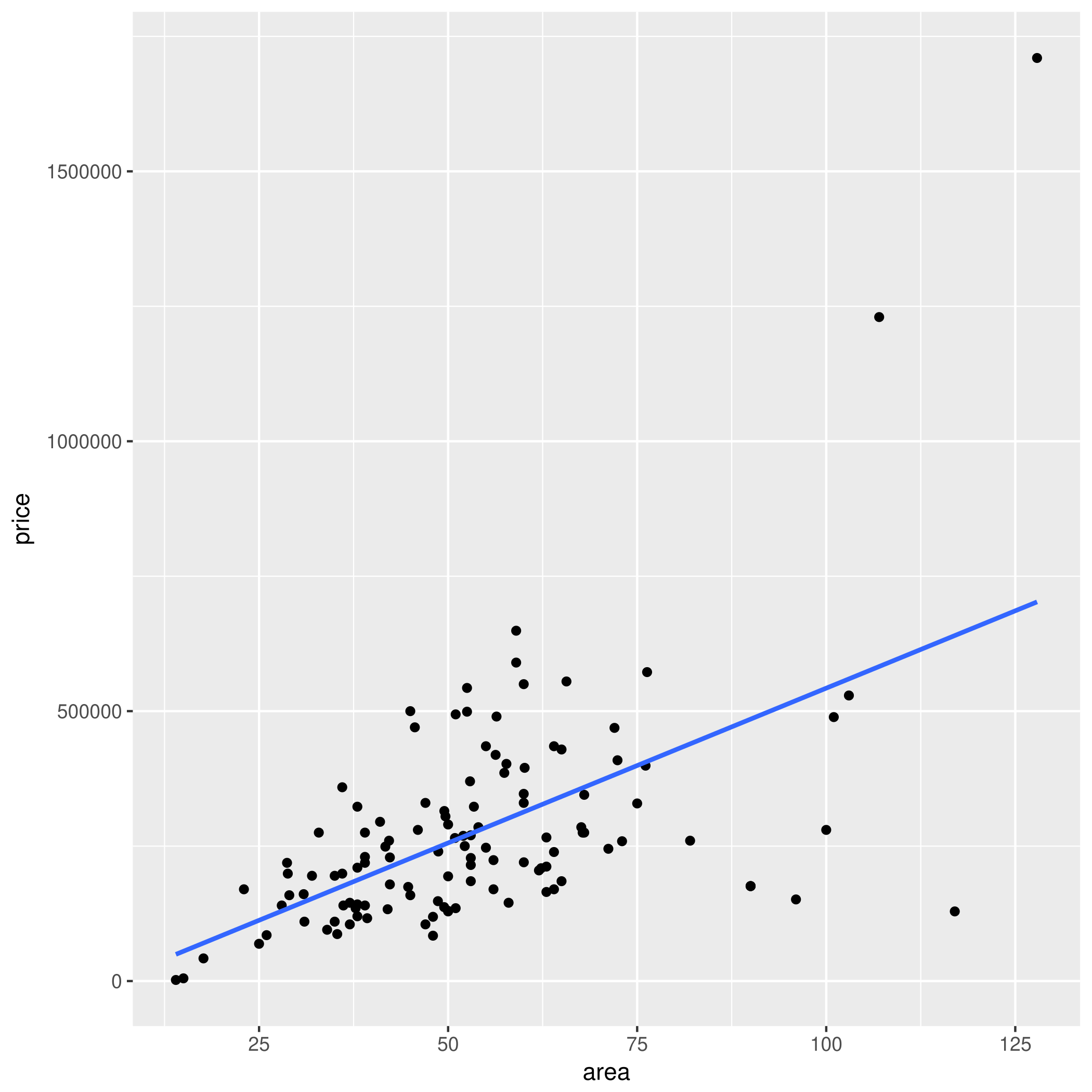
Regresja liniowa jest prosta...
... dosłownie — dopasuj prostą $y = ax + b$ do punktów
Należy odgadnąć $a$ i $b$ tak, aby zminimalizować błąd kwadratowy, tj. wartość:
$$\sum_{i=1}^n (y_i - (ax_i + b))^2$$
Regresje liniowa (jednej zmiennej) jest łatwa do rozwiązania — wystarczy podstawić do wzoru!
$$\hat{b} = \frac{ \sum_{i=1}^{n}{x_i y_i} - \frac{1}{n} \sum_{i=1}^n x_i \sum_{j=1}^n y_j}{ \sum_{i=1}^n {x_i^2} - \frac{1}{n} (\sum_{i=1}^n x_i)^2 }$$
$$\hat{a} = \bar{y} - \hat{b},\bar{x}$$
Na przykład dla mieszkań: $b =$ -30809.203 zł, $a =$ 5733.693 zł/m$^2$.
Regresja wielu zmiennych
W praktyce mamy do czynienia z wielowymiarową regresją liniową.
Cena mieszkań może być prognozowana na podstawie:
powierzchni ($x_1 = 32.3$)
liczby pokoi ($x_2 = 3$)
piętra ($x_3 = 4$)
wieku ($x_4 = 13$)
odległości od Dworca Centralnego w Warszawie ($x_5 = 371.3$)
cech zerojedynkowych:
czy wielka płyta? ($x_6 = 0$)
czy jest jacuzzi? ($x_7 = 1$)
czy jest grzyb? ($x_8 = 0$)
czy to Kielce? ($x_9 = 1$)
...
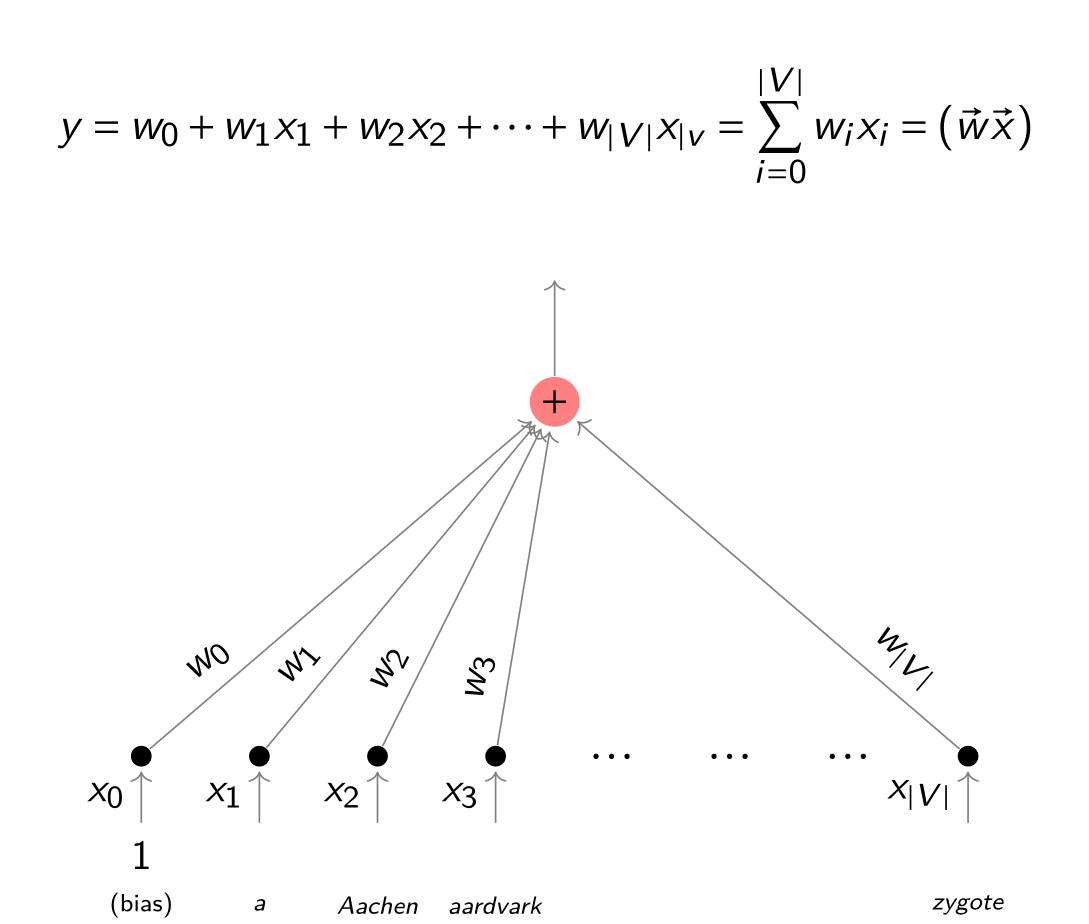
... więc uogólniamy na wiele ($k$) wymiarów:
$$ y = w_0 + w_1x_1 + \ldots + w_kx_k = w_0 + \sum_{j=1}^{k} w_jx_j $$
gdzie:
$x_1,\dots,x_k$ -- zmienne, na podstawie których zgadujemy
$w_0, w_1,\dots,w_k$ -- wagi modelu (do wymyślenia na podstawie przykładów)
$y$ -- odgadywana wartość
Też istnieje wzór ładny wzór na wyliczenie wektora wag!
$$\mathbf{w} = (\mathbf{X}^{\rm T}\mathbf{X})^{-1} \mathbf{X}^{\rm T}\mathbf{y}$$
... niestety odwracanie macierzy nie jest tanie :(
Kilka sporzeżeń
Regresja liniowa to najprostszy możliwy model:
im czegoś więcej na wejściu, tym proporcjonalnie (troszkę) więcej/mniej na wyjściu
nic prostszego nie da się wymyślić (funkcja stała??)
niestety model liniowy czasami kompletnie nie ma sensu (np. wzrost człowieka w stosunku do wieku)
Uczenie
A jak nauczyć się wag z przykładów?
- wzór (z odwracaniem macierzy) — problematyczny
Metoda gradientu prostego
Schodź wzdłuż lokalnego spadku funkcji błędu.
Tak więc w praktyce zamiast podstawiać do wzoru lepiej się uczyć iteracyjnie - metodą gradientu prostego (ang. _gradient descent).
- Zacznij od byle jakich wag $w_i$ (np. wylosuj)
- Weź losowy przykład uczący $x_1,\dots,x_n$, $y$.
- Oblicz wyjście $\hat{y}$ na podstawie $x_1,\dots,x_n$.
- Oblicz funkcję błędu między $y$ a $\hat{y}$.
- Zmodyfikuj lekko wagi $(w_i)$ w kierunku spadku funkcji błędu.
- Jeśli błąd jest duży, idź do 2.
Modyfikacja wag:
$$w_i := w_i - x_i (\hat{y} - y) \eta$$
gdzie $\eta$ to współczynnik uczenia _learning rate.
Ewaluacja regresji
To miary błędu (im mniej, tym lepiej!)}
Błąd bezwzględny (Mean Absolute Error, MAE)
$$\frac{1}{n}\sum_{i=1}^n |\hat{y}_i - y_i| $$
Mean Squared Error (MSE)
$$\frac{1}{n}\sum_{i=1}^n (\hat{y}_i - y_i)^2$$
Root Mean Squared Error (RMSE)
$$\sqrt{\frac{1}{n}\sum_{i=1}^n (\hat{y}_i - y_i)^2}$$
Regresja liniowa dla tekstu
Czym jest wektor $\vec{x} = (x_1,\dots,x_n)$? Wiemy, np. reprezentacja tf-idf (być z trikiem z haszowaniem, Word2vec etc.).