84 KiB
11. Sieci neuronowe – propagacja wsteczna
%matplotlib inline11.1. Metoda propagacji wstecznej – wprowadzenie
Architektura sieci neuronowych
- Budowa warstwowa, najczęściej sieci jednokierunkowe i gęste.
- Liczbę i rozmiar warstw dobiera się do każdego problemu.
- Rozmiary sieci określane poprzez liczbę neuronów lub parametrów.
_Feedforward
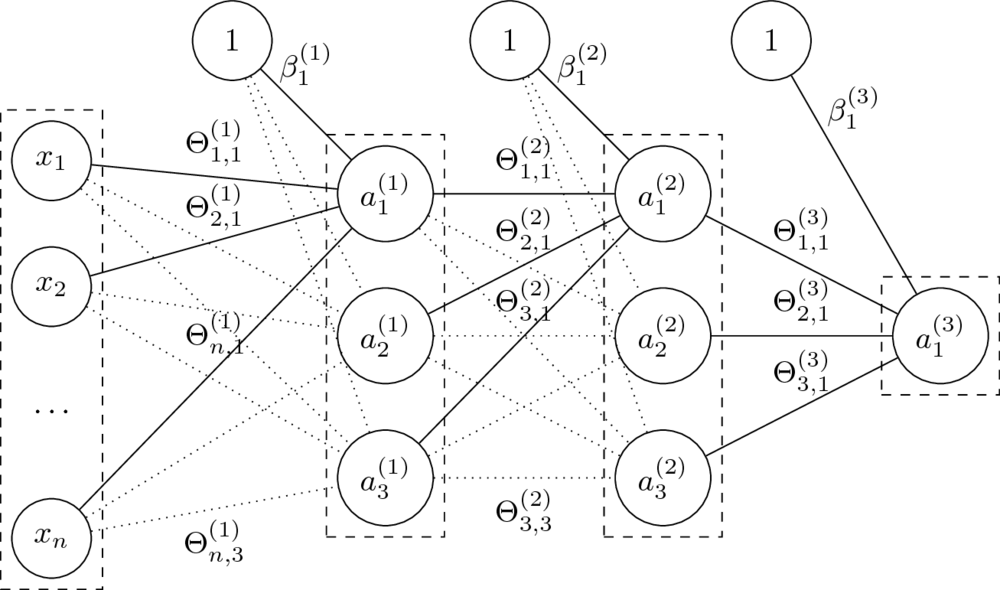
Mając daną $n$-warstwową sieć neuronową oraz jej parametry $\Theta^{(1)}, \ldots, \Theta^{(L)} $ oraz $\beta^{(1)}, \ldots, \beta^{(L)} $, obliczamy:
$$a^{(l)} = g^{(l)}\left( a^{(l-1)} \Theta^{(l)} + \beta^{(l)} \right). $$
- Funkcje $g^{(l)}$ to funkcje aktywacji.
Dla $i = 0$ przyjmujemy $a^{(0)} = x$ (wektor wierszowy cech) oraz $g^{(0)}(x) = x$ (identyczność).
- Parametry $\Theta$ to wagi na połączeniach miedzy neuronami dwóch warstw.
Rozmiar macierzy $\Theta^{(l)}$, czyli macierzy wag na połączeniach warstw $a^{(l-1)}$ i $a^{(l)}$, to $\dim(a^{(l-1)}) \times \dim(a^{(l)})$.
- Parametry $\beta$ zastępują tutaj dodawanie kolumny z jedynkami do macierzy cech.
Macierz $\beta^{(l)}$ ma rozmiar równy liczbie neuronów w odpowiedniej warstwie, czyli $1 \times \dim(a^{(l)})$.
- Klasyfikacja: dla ostatniej warstwy $L$ (o rozmiarze równym liczbie klas) przyjmuje się $g^{(L)}(x) = \mathop{\mathrm{softmax}}(x)$.
- Regresja: pojedynczy neuron wyjściowy; funkcją aktywacji może wtedy być np. funkcja identycznościowa.
Jak uczyć sieci neuronowe?
- W poznanych do tej pory algorytmach (regresja liniowa, regresja logistyczna) do uczenia używaliśmy funkcji kosztu, jej gradientu oraz algorytmu gradientu prostego (GD/SGD)
- Dla sieci neuronowych potrzebowalibyśmy również znaleźć gradient funkcji kosztu.
- Sprowadza się to do bardziej ogólnego problemu:
jak obliczyć gradient $\nabla f(x)$ dla danej funkcji $f$ i wektora wejściowego $x$?
Pochodna funkcji
- Pochodna mierzy, jak szybko zmienia się wartość funkcji względem zmiany jej argumentów:
$$ \frac{d f(x)}{d x} = \lim_{h \to 0} \frac{ f(x + h) - f(x) }{ h } $$
Pochodna cząstkowa i gradient
- Pochodna cząstkowa mierzy, jak szybko zmienia się wartość funkcji względem zmiany jej _pojedynczego argumentu.
- Gradient to wektor pochodnych cząstkowych:
$$ \nabla f = \left( \frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right) $$
Gradient – przykłady
$$ f(x_1, x_2) = x_1 + x_2 \qquad \to \qquad \frac{\partial f}{\partial x_1} = 1, \quad \frac{\partial f}{\partial x_2} = 1, \quad \nabla f = (1, 1) $$
$$ f(x_1, x_2) = x_1 \cdot x_2 \qquad \to \qquad \frac{\partial f}{\partial x_1} = x_2, \quad \frac{\partial f}{\partial x_2} = x_1, \quad \nabla f = (x_2, x_1) $$
Własności pochodnych cząstkowych
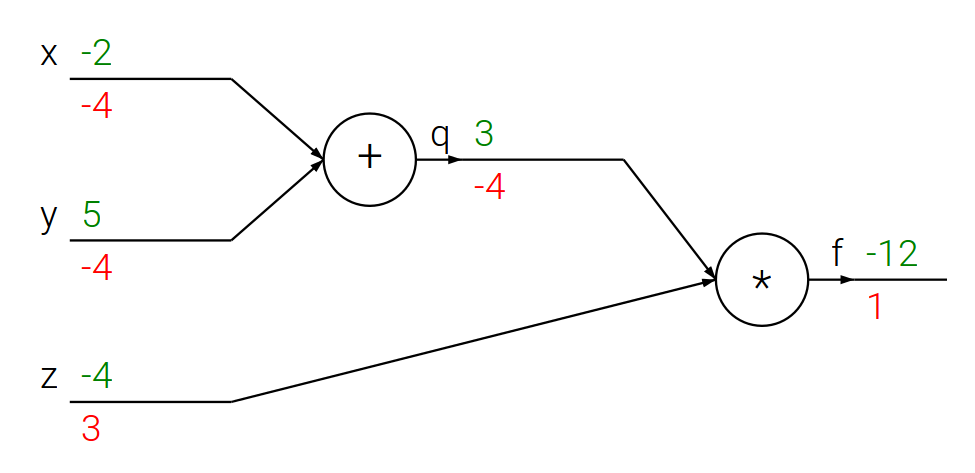
Jezeli $f(x, y, z) = (x + y) , z$ oraz $x + y = q$, to: $$f = q z, \quad \frac{\partial f}{\partial q} = z, \quad \frac{\partial f}{\partial z} = q, \quad \frac{\partial q}{\partial x} = 1, \quad \frac{\partial q}{\partial y} = 1 $$
Reguła łańcuchowa
$$ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} , \frac{\partial q}{\partial x}, \quad \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} , \frac{\partial q}{\partial y} $$
Propagacja wsteczna – prosty przykład
# Dla ustalonego wejścia
x = -2
y = 5
z = -4# Krok w przód
q = x + y
f = q * z
print(q, f)3 -12
# Propagacja wsteczna dla f = q * z
# Oznaczmy symbolami `dfx`, `dfy`, `dfz`, `dfq` odpowiednio
# pochodne cząstkowe ∂f/∂x, ∂f/∂y, ∂f/∂z, ∂f/∂q
dfz = q
dfq = z
# Propagacja wsteczna dla q = x + y
dfx = 1 * dfq # z reguły łańcuchowej
dfy = 1 * dfq # z reguły łańcuchowej
print([dfx, dfy, dfz])[-4, -4, 3]
- Właśnie tak wygląda obliczanie pochodnych metodą propagacji wstecznej!
- Spróbujmy czegoś bardziej skomplikowanego:
metodą propagacji wstecznej obliczmy pochodną funkcji sigmoidalnej.
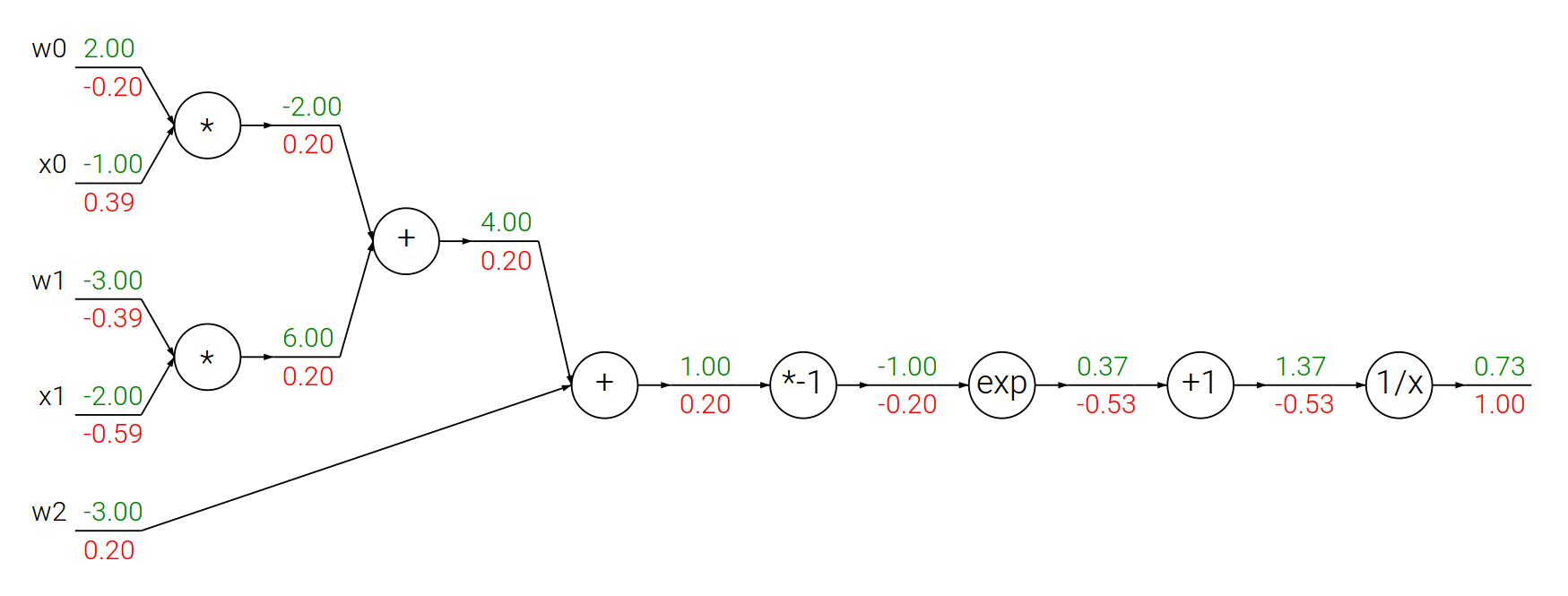
Propagacja wsteczna – funkcja sigmoidalna
Funkcja sigmoidalna:
$$f(\theta,x) = \frac{1}{1+e^{-(\theta_0 x_0 + \theta_1 x_1 + \theta_2)}}$$
$$ \begin{array}{lcl} f(x) = \frac{1}{x} \quad & \rightarrow & \quad \frac{df}{dx} = -\frac{1}{x^2} \\ f_c(x) = c + x \quad & \rightarrow & \quad \frac{df}{dx} = 1 \\ f(x) = e^x \quad & \rightarrow & \quad \frac{df}{dx} = e^x \\ f_a(x) = ax \quad & \rightarrow & \quad \frac{df}{dx} = a \\ \end{array} $$
from math import exp
# Losowe wagi i dane
w = [2, -3, -3]
x = [-1, -2]
# Krok w przód
dot = w[0] * x[0] + w[1] * x[1] + w[2]
f = 1.0 / (1 + exp(-dot)) # funkcja sigmoidalna
# Krok w tył
ddot = (1 - f) * f # pochodna funkcji sigmoidalnej
dx = [w[0] * ddot, w[1] * ddot]
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot]
print(dx)
print(dw)[0.3932238664829637, -0.5898357997244456] [-0.19661193324148185, -0.3932238664829637, 0.19661193324148185]
Obliczanie gradientów – podsumowanie
- Gradient $f$ dla $x$ mówi, jak zmieni się całe wyrażenie przy zmianie wartości $x$.
- Gradienty łączymy, korzystając z reguły łańcuchowej.
- W kroku "wstecz" gradienty informują, które części grafu powinny być zwiększone lub zmniejszone (i z jaką siłą), aby zwiększyć wartość na wyjściu.
- W kontekście implementacji chcemy dzielić funkcję $f$ na części, dla których można łatwo obliczyć gradienty.
11.2. Uczenie wielowarstwowych sieci neuronowych metodą propagacji wstecznej
Mając algorytm SGD oraz gradienty wszystkich wag, moglibyśmy trenować każdą sieć.
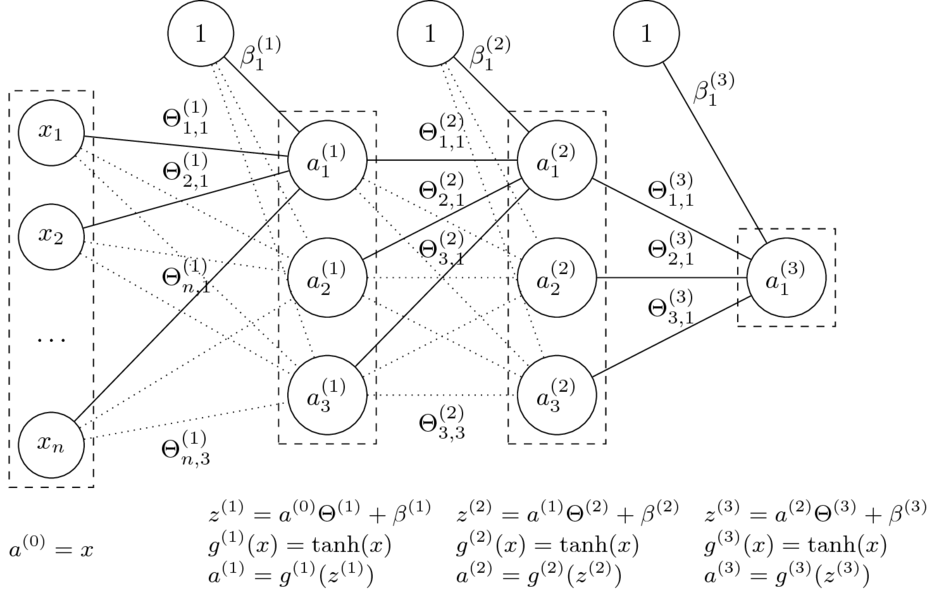
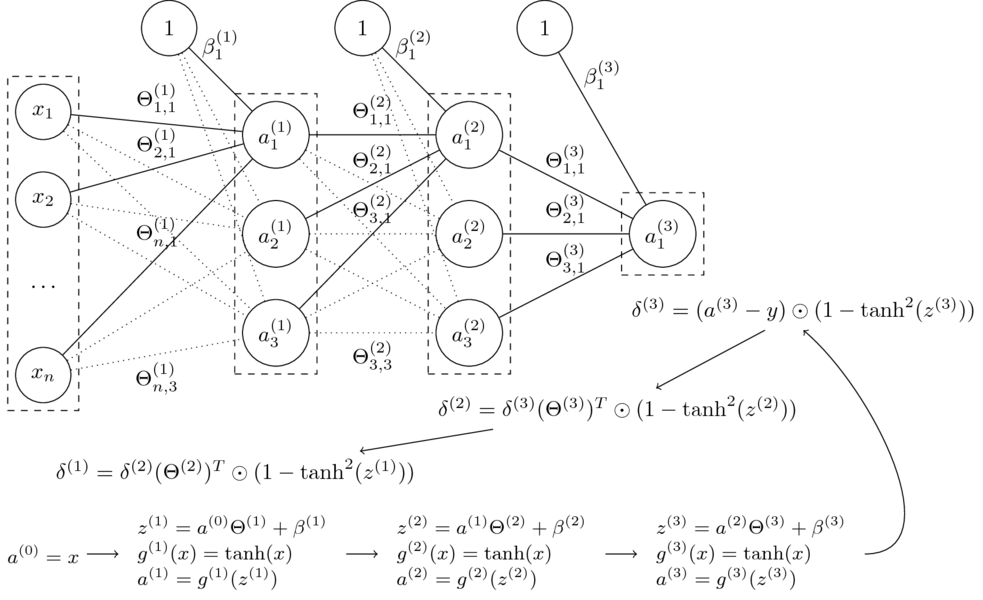
- Niech $\Theta = (\Theta^{(1)},\Theta^{(2)},\Theta^{(3)},\beta^{(1)},\beta^{(2)},\beta^{(3)})$
- Funkcja sieci neuronowej z grafiki: $$\small h_\Theta(x) = \tanh(\tanh(\tanh(x\Theta^{(1)}+\beta^{(1)})\Theta^{(2)} + \beta^{(2)})\Theta^{(3)} + \beta^{(3)})$$
- Funkcja kosztu dla regresji: $$J(\Theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h_\Theta(x^{(i)})- y^{(i)})^2 $$
- Jak obliczymy gradienty?
$$\nabla_{\Theta^{(l)}} J(\Theta) = ? \quad \nabla_{\beta^{(l)}} J(\Theta) = ?$$
W kierunku propagacji wstecznej
- Pewna (niewielka) zmiana wagi $\Delta z^l_j$ dla $j$-ego neuronu w warstwie $l$ pociąga za sobą (niewielką) zmianę kosztu:
$$\frac{\partial J(\Theta)}{\partial z^{l}_j} \Delta z^{l}_j$$
- Jeżeli $\frac{\partial J(\Theta)}{\partial z^{l}_j}$ jest duża, $\Delta z^l_j$ ze znakiem przeciwnym zredukuje koszt.
- Jeżeli $\frac{\partial J(\Theta)}{\partial z^l_j}$ jest bliska zeru, koszt nie będzie mocno poprawiony.
- Definiujemy błąd $\delta^l_j$ neuronu $j$ w warstwie $l$:
$$\delta^l_j := \dfrac{\partial J(\Theta)}{\partial z^l_j}$$ $$\delta^l := \nabla_{z^l} J(\Theta) \quad \textrm{ (zapis wektorowy)} $$
Podstawowe równania propagacji wstecznej
$$ \begin{array}{rcll} \delta^L & = & \nabla_{a^L}J(\Theta) \odot { \left( g^{L} \right) }^{\prime} \left( z^L \right) & (BP1) \\[2mm] \delta^{l} & = & \left( \left( \Theta^{l+1} \right) ! ^\top , \delta^{l+1} \right) \odot {{ \left( g^{l} \right) }^{\prime}} \left( z^{l} \right) & (BP2)\\[2mm] \nabla_{\beta^l} J(\Theta) & = & \delta^l & (BP3)\\[2mm] \nabla_{\Theta^l} J(\Theta) & = & a^{l-1} \odot \delta^l & (BP4)\\ \end{array} $$
(BP1)
$$ \delta^L_j ; = ; \frac{ \partial J }{ \partial a^L_j } , g' !! \left( z^L_j \right) $$ $$ \delta^L ; = ; \nabla_{a^L}J(\Theta) \odot { \left( g^{L} \right) }^{\prime} \left( z^L \right) $$ Błąd w ostatniej warstwie jest iloczynem szybkości zmiany kosztu względem $j$-tego wyjścia i szybkości zmiany funkcji aktywacji w punkcie $z^L_j$.
(BP2)
$$ \delta^{l} ; = ; \left( \left( \Theta^{l+1} \right) ! ^\top , \delta^{l+1} \right) \odot {{ \left( g^{l} \right) }^{\prime}} \left( z^{l} \right) $$ Aby obliczyć błąd w $l$-tej warstwie, należy przemnożyć błąd z następnej ($(l+1)$-szej) warstwy przez transponowany wektor wag, a uzyskaną macierz pomnożyć po współrzędnych przez szybkość zmiany funkcji aktywacji w punkcie $z^l$.
(BP3)
$$ \nabla_{\beta^l} J(\Theta) ; = ; \delta^l $$ Błąd w $l$-tej warstwie jest równy wartości gradientu funkcji kosztu.
(BP4)
$$ \nabla_{\Theta^l} J(\Theta) ; = ; a^{l-1} \odot \delta^l $$ Gradient funkcji kosztu względem wag $l$-tej warstwy można obliczyć jako iloczyn po współrzędnych $a^{l-1}$ przez $\delta^l$.
Algorytm propagacji wstecznej
Dla pojedynczego przykładu $(x,y)$:
- Wejście: Ustaw aktywacje w warstwie cech $a^{(0)}=x$
- Feedforward: dla $l=1,\dots,L$ oblicz $z^{(l)} = a^{(l-1)} \Theta^{(l)} + \beta^{(l)}$ oraz $a^{(l)}=g^{(l)} !! \left( z^{(l)} \right)$
- Błąd wyjścia $\delta^{(L)}$: oblicz wektor $$\delta^{(L)}= \nabla_{a^{(L)}}J(\Theta) \odot {g^{\prime}}^{(L)} !! \left( z^{(L)} \right) $$
- Propagacja wsteczna błędu: dla $l = L-1,L-2,\dots,1$ oblicz $$\delta^{(l)} = \delta^{(l+1)}(\Theta^{(l+1)})^T \odot {g^{\prime}}^{(l)} !! \left( z^{(l)} \right) $$
- Gradienty:
- $\dfrac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = a_i^{(l-1)}\delta_j^{(l)} \textrm{ oraz } \dfrac{\partial}{\partial \beta_{j}^{(l)}} J(\Theta) = \delta_j^{(l)}$
W naszym przykładzie:
$$\small J(\Theta) = \frac{1}{2} \left( a^{(L)} - y \right) ^2 $$ $$\small \dfrac{\partial}{\partial a^{(L)}} J(\Theta) = a^{(L)} - y$$
$$\small \tanh^{\prime}(x) = 1 - \tanh^2(x)$$
Algorytm SGD z propagacją wsteczną
Pojedyncza iteracja:
- Dla parametrów $\Theta = (\Theta^{(1)},\ldots,\Theta^{(L)})$ utwórz pomocnicze macierze zerowe $\Delta = (\Delta^{(1)},\ldots,\Delta^{(L)})$ o takich samych wymiarach (dla uproszczenia opuszczono wagi $\beta$).
- Dla $m$ przykładów we wsadzie (_batch), $i = 1,\ldots,m$:
- Wykonaj algortym propagacji wstecznej dla przykładu $(x^{(i)}, y^{(i)})$ i przechowaj gradienty $\nabla_{\Theta}J^{(i)}(\Theta)$ dla tego przykładu;
- $\Delta := \Delta + \dfrac{1}{m}\nabla_{\Theta}J^{(i)}(\Theta)$
- Wykonaj aktualizację wag: $\Theta := \Theta - \alpha \Delta$
Propagacja wsteczna – podsumowanie
- Algorytm pierwszy raz wprowadzony w latach 70. XX w.
- W 1986 David Rumelhart, Geoffrey Hinton i Ronald Williams pokazali, że jest znacznie szybszy od wcześniejszych metod.
- Obecnie najpopularniejszy algorytm uczenia sieci neuronowych.
11.3. Przykłady implementacji wielowarstwowych sieci neuronowych
Uwaga!
Poniższe przykłady wykorzystują interfejs Keras, który jest częścią biblioteki TensorFlow.
Aby uruchomić TensorFlow w środowisku Jupyter, należy wykonać następujące czynności:
Przed pierwszym uruchomieniem (wystarczy wykonać tylko raz)
Instalacja biblioteki TensorFlow w środowisku Anaconda:
- Uruchom _Anaconda Navigator
- Wybierz kafelek _CMD.exe Prompt
- Kliknij przycisk _Launch
- Pojawi się konsola. Wpisz następujące polecenia, każde zatwierdzając wciśnięciem klawisza Enter:
conda create -n tf tensorflow conda activate tf conda install pandas matplotlib jupyter notebook
Przed każdym uruchomieniem
Jeżeli chcemy korzystać z biblioteki TensorFlow, to środowisko Jupyter Notebook należy uruchomić w następujący sposób:
- Uruchom _Anaconda Navigator
- Wybierz kafelek _CMD.exe Prompt
- Kliknij przycisk _Launch
- Pojawi się konsola. Wpisz następujące polecenia, każde zatwierdzając wciśnięciem klawisza Enter:
conda activate tf jupyter notebook
Przykład: MNIST
_Modified National Institute of Standards and Technology database
- Zbiór cyfr zapisanych pismem odręcznym
- 60 000 przykładów uczących, 10 000 przykładów testowych
- Rozdzielczość każdego przykładu: 28 × 28 = 784 piksele
from tensorflow import keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense, Dropout
# załaduj dane i podziel je na zbiory uczący i testowy
(x_train, y_train), (x_test, y_test) = mnist.load_data()2023-01-26 10:52:17.922141: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: AVX2 FMA To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags. 2023-01-26 10:52:18.163925: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory 2023-01-26 10:52:18.163996: I tensorflow/compiler/xla/stream_executor/cuda/cudart_stub.cc:29] Ignore above cudart dlerror if you do not have a GPU set up on your machine. 2023-01-26 10:52:19.577890: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2023-01-26 10:52:19.578662: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2023-01-26 10:52:19.578677: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11490434/11490434 [==============================] - 1s 0us/step
from matplotlib import pyplot as plt
def draw_examples(examples, captions=None):
plt.figure(figsize=(16, 4))
m = len(examples)
for i, example in enumerate(examples):
plt.subplot(100 + m * 10 + i + 1)
plt.imshow(example, cmap=plt.get_cmap("gray"))
plt.show()
if captions is not None:
print(6 * " " + (10 * " ").join(str(captions[i]) for i in range(m)))draw_examples(x_train[:7], captions=y_train)5 0 4 1 9 2 1
num_classes = 10
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype("float32")
x_test = x_test.astype("float32")
x_train /= 255
x_test /= 255
print("{} przykładów uczących".format(x_train.shape[0]))
print("{} przykładów testowych".format(x_test.shape[0]))
# przekonwertuj wektory klas na binarne macierze klas
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)60000 przykładów uczących 10000 przykładów testowych
model = keras.Sequential()
model.add(Dense(512, activation="relu", input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation="softmax"))
model.summary()2023-01-26 10:52:27.077963: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcuda.so.1'; dlerror: libcuda.so.1: cannot open shared object file: No such file or directory 2023-01-26 10:52:27.078089: W tensorflow/compiler/xla/stream_executor/cuda/cuda_driver.cc:265] failed call to cuInit: UNKNOWN ERROR (303) 2023-01-26 10:52:27.078807: I tensorflow/compiler/xla/stream_executor/cuda/cuda_diagnostics.cc:156] kernel driver does not appear to be running on this host (ELLIOT): /proc/driver/nvidia/version does not exist 2023-01-26 10:52:27.095828: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: AVX2 FMA To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 512) 401920
dense_1 (Dense) (None, 512) 262656
dense_2 (Dense) (None, 10) 5130
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
print(x_train.shape, y_train.shape)(60000, 784) (60000, 10)
model.compile(
loss="categorical_crossentropy",
optimizer=keras.optimizers.RMSprop(),
metrics=["accuracy"],
)
model.fit(
x_train,
y_train,
batch_size=128,
epochs=5,
verbose=1,
validation_data=(x_test, y_test),
)2023-01-26 10:52:27.713204: W tensorflow/tsl/framework/cpu_allocator_impl.cc:82] Allocation of 188160000 exceeds 10% of free system memory.
Epoch 1/5 469/469 [==============================] - 13s 25ms/step - loss: 0.2303 - accuracy: 0.9290 - val_loss: 0.1023 - val_accuracy: 0.9684 Epoch 2/5 469/469 [==============================] - 9s 20ms/step - loss: 0.0840 - accuracy: 0.9742 - val_loss: 0.0794 - val_accuracy: 0.9754 Epoch 3/5 469/469 [==============================] - 9s 20ms/step - loss: 0.0548 - accuracy: 0.9826 - val_loss: 0.0603 - val_accuracy: 0.9828 Epoch 4/5 469/469 [==============================] - 9s 20ms/step - loss: 0.0367 - accuracy: 0.9883 - val_loss: 0.0707 - val_accuracy: 0.9796 Epoch 5/5 469/469 [==============================] - 9s 19ms/step - loss: 0.0278 - accuracy: 0.9912 - val_loss: 0.0765 - val_accuracy: 0.9785
<keras.callbacks.History at 0x7f8642785120>
score = model.evaluate(x_test, y_test, verbose=0)
print("Test loss: {}".format(score[0]))
print("Test accuracy: {}".format(score[1]))Test loss: 0.07645954936742783 Test accuracy: 0.9785000085830688
Warstwa _dropout to metoda regularyzacji, służy zapobieganiu nadmiernemu dopasowaniu sieci. Polega na tym, że część węzłów sieci jest usuwana w sposób losowy.
# Bez warstw Dropout
num_classes = 10
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype("float32")
x_test = x_test.astype("float32")
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model_no_dropout = keras.Sequential()
model_no_dropout.add(Dense(512, activation="relu", input_shape=(784,)))
model_no_dropout.add(Dense(512, activation="relu"))
model_no_dropout.add(Dense(num_classes, activation="softmax"))
model_no_dropout.summary()
model_no_dropout.compile(
loss="categorical_crossentropy",
optimizer=keras.optimizers.RMSprop(),
metrics=["accuracy"],
)
model_no_dropout.fit(
x_train,
y_train,
batch_size=128,
epochs=5,
verbose=1,
validation_data=(x_test, y_test),
)Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_3 (Dense) (None, 512) 401920
dense_4 (Dense) (None, 512) 262656
dense_5 (Dense) (None, 10) 5130
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
Epoch 1/5
2023-01-26 10:53:20.710986: W tensorflow/tsl/framework/cpu_allocator_impl.cc:82] Allocation of 188160000 exceeds 10% of free system memory.
469/469 [==============================] - 10s 19ms/step - loss: 0.2283 - accuracy: 0.9302 - val_loss: 0.0983 - val_accuracy: 0.9685 Epoch 2/5 469/469 [==============================] - 10s 22ms/step - loss: 0.0849 - accuracy: 0.9736 - val_loss: 0.0996 - val_accuracy: 0.9673 Epoch 3/5 469/469 [==============================] - 10s 22ms/step - loss: 0.0549 - accuracy: 0.9829 - val_loss: 0.0704 - val_accuracy: 0.9777 Epoch 4/5 469/469 [==============================] - 10s 21ms/step - loss: 0.0380 - accuracy: 0.9877 - val_loss: 0.0645 - val_accuracy: 0.9797 Epoch 5/5 469/469 [==============================] - 20s 43ms/step - loss: 0.0276 - accuracy: 0.9910 - val_loss: 0.0637 - val_accuracy: 0.9825
<keras.callbacks.History at 0x7f86301a3f40>
# Bez warstw Dropout
score = model_no_dropout.evaluate(x_test, y_test, verbose=0)
print("Test loss (no dropout): {}".format(score[0]))
print("Test accuracy (no dropout): {}".format(score[1]))Test loss (no dropout): 0.06374581903219223 Test accuracy (no dropout): 0.9825000166893005
# Więcej warstw, inna funkcja aktywacji
num_classes = 10
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) # 784 = 28 * 28
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype("float32")
x_test = x_test.astype("float32")
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model3 = keras.Sequential()
model3.add(Dense(2500, activation="tanh", input_shape=(784,)))
model3.add(Dense(2000, activation="tanh"))
model3.add(Dense(1500, activation="tanh"))
model3.add(Dense(1000, activation="tanh"))
model3.add(Dense(500, activation="tanh"))
model3.add(Dense(num_classes, activation="softmax"))
model3.summary()
model3.compile(
loss="categorical_crossentropy",
optimizer=keras.optimizers.RMSprop(),
metrics=["accuracy"],
)
model3.fit(
x_train,
y_train,
batch_size=128,
epochs=10,
verbose=1,
validation_data=(x_test, y_test),
)Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_6 (Dense) (None, 2500) 1962500
dense_7 (Dense) (None, 2000) 5002000
dense_8 (Dense) (None, 1500) 3001500
dense_9 (Dense) (None, 1000) 1501000
dense_10 (Dense) (None, 500) 500500
dense_11 (Dense) (None, 10) 5010
=================================================================
Total params: 11,972,510
Trainable params: 11,972,510
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
2023-01-26 11:06:02.193383: W tensorflow/tsl/framework/cpu_allocator_impl.cc:82] Allocation of 188160000 exceeds 10% of free system memory.
469/469 [==============================] - 140s 294ms/step - loss: 0.6488 - accuracy: 0.8175 - val_loss: 0.2686 - val_accuracy: 0.9211 Epoch 2/10 469/469 [==============================] - 147s 313ms/step - loss: 0.2135 - accuracy: 0.9367 - val_loss: 0.2251 - val_accuracy: 0.9363 Epoch 3/10 469/469 [==============================] - 105s 224ms/step - loss: 0.1549 - accuracy: 0.9535 - val_loss: 0.1535 - val_accuracy: 0.9533 Epoch 4/10 469/469 [==============================] - 94s 200ms/step - loss: 0.1210 - accuracy: 0.9635 - val_loss: 0.1412 - val_accuracy: 0.9599 Epoch 5/10 469/469 [==============================] - 93s 199ms/step - loss: 0.0985 - accuracy: 0.9704 - val_loss: 0.1191 - val_accuracy: 0.9650 Epoch 6/10 469/469 [==============================] - 105s 224ms/step - loss: 0.0834 - accuracy: 0.9746 - val_loss: 0.0959 - val_accuracy: 0.9732 Epoch 7/10 469/469 [==============================] - 111s 236ms/step - loss: 0.0664 - accuracy: 0.9797 - val_loss: 0.1071 - val_accuracy: 0.9685 Epoch 8/10 469/469 [==============================] - 184s 392ms/step - loss: 0.0562 - accuracy: 0.9824 - val_loss: 0.0951 - val_accuracy: 0.9737 Epoch 9/10 469/469 [==============================] - 161s 344ms/step - loss: 0.0475 - accuracy: 0.9852 - val_loss: 0.1377 - val_accuracy: 0.9631 Epoch 10/10 469/469 [==============================] - 146s 311ms/step - loss: 0.0399 - accuracy: 0.9873 - val_loss: 0.1093 - val_accuracy: 0.9736
<keras.callbacks.History at 0x7f8640136f50>
# Więcej warstw, inna funkcja aktywacji
score = model3.evaluate(x_test, y_test, verbose=0)
print("Test loss: {}".format(score[0]))
print("Test accuracy: {}".format(score[1]))Test loss: 0.10930903255939484 Test accuracy: 0.9735999703407288
Przykład: 4-pikselowy aparat fotograficzny
def generate_example(description):
variant = random.choice([1, -1])
if description == "s": # solid
return (
np.array([[1.0, 1.0], [1.0, 1.0]])
if variant == 1
else np.array([[-1.0, -1.0], [-1.0, -1.0]])
)
elif description == "v": # vertical
return (
np.array([[1.0, -1.0], [1.0, -1.0]])
if variant == 1
else np.array([[-1.0, 1.0], [-1.0, 1.0]])
)
elif description == "d": # diagonal
return (
np.array([[1.0, -1.0], [-1.0, 1.0]])
if variant == 1
else np.array([[-1.0, 1.0], [1.0, -1.0]])
)
elif description == "h": # horizontal
return (
np.array([[1.0, 1.0], [-1.0, -1.0]])
if variant == 1
else np.array([[-1.0, -1.0], [1.0, 1.0]])
)
else:
return np.array(
[
[random.uniform(-1, 1), random.uniform(-1, 1)],
[random.uniform(-1, 1), random.uniform(-1, 1)],
]
)import numpy as np
import random
num_classes = 4
trainset_size = 4000
testset_size = 1000
y4_train = np.array([random.choice(["s", "v", "d", "h"]) for i in range(trainset_size)])
x4_train = np.array([generate_example(desc) for desc in y4_train])
y4_test = np.array([random.choice(["s", "v", "d", "h"]) for i in range(testset_size)])
x4_test = np.array([generate_example(desc) for desc in y4_test])draw_examples(x4_train[:7], captions=y4_train)d h h d h d h
x4_train = x4_train.reshape(trainset_size, 4)
x4_test = x4_test.reshape(testset_size, 4)
x4_train = x4_train.astype("float32")
x4_test = x4_test.astype("float32")
y4_train = np.array([{"s": 0, "v": 1, "d": 2, "h": 3}[desc] for desc in y4_train])
y4_test = np.array([{"s": 0, "v": 1, "d": 2, "h": 3}[desc] for desc in y4_test])
y4_train = keras.utils.to_categorical(y4_train, num_classes)
y4_test = keras.utils.to_categorical(y4_test, num_classes)model4 = keras.Sequential()
model4.add(Dense(4, activation="tanh", input_shape=(4,)))
model4.add(Dense(4, activation="tanh"))
model4.add(Dense(8, activation="relu"))
model4.add(Dense(num_classes, activation="softmax"))
model4.summary()Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_12 (Dense) (None, 4) 20
dense_13 (Dense) (None, 4) 20
dense_14 (Dense) (None, 8) 40
dense_15 (Dense) (None, 4) 36
=================================================================
Total params: 116
Trainable params: 116
Non-trainable params: 0
_________________________________________________________________
model4.layers[0].set_weights(
[
np.array(
[
[1.0, 0.0, 1.0, 0.0],
[0.0, 1.0, 0.0, 1.0],
[1.0, 0.0, -1.0, 0.0],
[0.0, 1.0, 0.0, -1.0],
],
dtype=np.float32,
),
np.array([0.0, 0.0, 0.0, 0.0], dtype=np.float32),
]
)
model4.layers[1].set_weights(
[
np.array(
[
[1.0, -1.0, 0.0, 0.0],
[1.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 1.0, -1.0],
[0.0, 0.0, -1.0, -1.0],
],
dtype=np.float32,
),
np.array([0.0, 0.0, 0.0, 0.0], dtype=np.float32),
]
)
model4.layers[2].set_weights(
[
np.array(
[
[1.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 1.0, -1.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0, -1.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, -1.0],
],
dtype=np.float32,
),
np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], dtype=np.float32),
]
)model4.layers[3].set_weights(
[
np.array(
[
[1.0, 0.0, 0.0, 0.0],
[1.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0],
[0.0, 0.0, 0.0, 1.0],
],
dtype=np.float32,
),
np.array([0.0, 0.0, 0.0, 0.0], dtype=np.float32),
]
)
model4.compile(
loss="categorical_crossentropy",
optimizer=keras.optimizers.Adagrad(),
metrics=["accuracy"],
)for layer in model4.layers:
print(layer.get_weights())[array([[ 1., 0., 1., 0.],
[ 0., 1., 0., 1.],
[ 1., 0., -1., 0.],
[ 0., 1., 0., -1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
[array([[ 1., -1., 0., 0.],
[ 1., 1., 0., 0.],
[ 0., 0., 1., -1.],
[ 0., 0., -1., -1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
[array([[ 1., -1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 1., -1., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 1., -1., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 1., -1.]], dtype=float32), array([0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)]
[array([[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)]
model4.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])1/1 [==============================] - 1s 872ms/step
array([[0.17831734, 0.17831734, 0.17831734, 0.465048 ]], dtype=float32)
score = model4.evaluate(x4_test, y4_test, verbose=0)
print("Test loss: {}".format(score[0]))
print("Test accuracy: {}".format(score[1]))Test loss: 0.7656148672103882 Test accuracy: 1.0
model5 = keras.Sequential()
model5.add(Dense(4, activation="tanh", input_shape=(4,)))
model5.add(Dense(4, activation="tanh"))
model5.add(Dense(8, activation="relu"))
model5.add(Dense(num_classes, activation="softmax"))
model5.compile(
loss="categorical_crossentropy",
optimizer=keras.optimizers.RMSprop(),
metrics=["accuracy"],
)
model5.summary()Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_16 (Dense) (None, 4) 20
dense_17 (Dense) (None, 4) 20
dense_18 (Dense) (None, 8) 40
dense_19 (Dense) (None, 4) 36
=================================================================
Total params: 116
Trainable params: 116
Non-trainable params: 0
_________________________________________________________________
model5.fit(x4_train, y4_train, epochs=8, validation_data=(x4_test, y4_test))Epoch 1/8 125/125 [==============================] - 3s 8ms/step - loss: 1.3014 - accuracy: 0.4947 - val_loss: 1.1876 - val_accuracy: 0.6040 Epoch 2/8 125/125 [==============================] - 1s 6ms/step - loss: 1.0779 - accuracy: 0.7395 - val_loss: 0.9865 - val_accuracy: 0.8730 Epoch 3/8 125/125 [==============================] - 1s 4ms/step - loss: 0.8925 - accuracy: 0.8382 - val_loss: 0.8114 - val_accuracy: 0.7460 Epoch 4/8 125/125 [==============================] - 0s 4ms/step - loss: 0.7266 - accuracy: 0.8060 - val_loss: 0.6622 - val_accuracy: 0.8730 Epoch 5/8 125/125 [==============================] - 0s 4ms/step - loss: 0.5890 - accuracy: 0.8765 - val_loss: 0.5392 - val_accuracy: 0.8730 Epoch 6/8 125/125 [==============================] - 1s 4ms/step - loss: 0.4738 - accuracy: 0.8838 - val_loss: 0.4293 - val_accuracy: 0.8730 Epoch 7/8 125/125 [==============================] - 1s 5ms/step - loss: 0.3636 - accuracy: 0.9337 - val_loss: 0.3191 - val_accuracy: 1.0000 Epoch 8/8 125/125 [==============================] - 1s 5ms/step - loss: 0.2606 - accuracy: 1.0000 - val_loss: 0.2202 - val_accuracy: 1.0000
<keras.callbacks.History at 0x7f860a6a9870>
model5.predict([np.array([[1.0, 1.0], [-1.0, -1.0]]).reshape(1, 4)])1/1 [==============================] - 0s 106ms/step
array([[1.5366691e-01, 4.4674356e-04, 4.7448810e-02, 7.9843748e-01]],
dtype=float32)score = model5.evaluate(x4_test, y4_test, verbose=0)
print("Test loss: {}".format(score[0]))
print("Test accuracy: {}".format(score[1]))Test loss: 0.22015966475009918 Test accuracy: 1.0
import contextlib
@contextlib.contextmanager
def printoptions(*args, **kwargs):
original = np.get_printoptions()
np.set_printoptions(*args, **kwargs)
try:
yield
finally:
np.set_printoptions(**original)with printoptions(precision=1, suppress=True):
for layer in model5.layers:
print(layer.get_weights())[array([[-0.8, 0.1, -0.6, 0.1],
[-0.9, -0.7, -1. , 0.6],
[-0.3, 0.5, 0.5, 0.3],
[ 0.4, 0.3, -0.9, -0.8]], dtype=float32), array([ 0., -0., 0., 0.], dtype=float32)]
[array([[-1.1, 1.2, -0.6, -0.6],
[-1.1, -0.2, -0.7, -1.3],
[ 0.6, 0.9, 0.3, -1.3],
[ 0.8, 0.3, 0.7, 0.4]], dtype=float32), array([ 0.3, 0.5, -0.4, 0.5], dtype=float32)]
[array([[ 0.5, 0.4, -0.4, 0.3, 0.8, -1.4, -1.1, 0.8],
[ 0.5, -1.3, 0.3, 0.4, -1.3, 0.2, 0.9, 0.7],
[-0.2, -0.1, -0.5, -0.2, 1.2, -0.4, -0.4, 1.1],
[-1.1, 0.4, 1.3, -1.1, 1. , -1.1, -0.8, 0.3]], dtype=float32), array([ 0.2, 0.2, 0.1, 0.1, 0.2, 0.1, -0.2, 0. ], dtype=float32)]
[array([[ 0.7, 0.8, -1.5, -0.2],
[ 0.7, -0.9, -1.2, 0.2],
[-0.4, 1.1, -0.1, -1.6],
[ 0.3, 0.8, -1.4, 0.4],
[ 0.2, -1.4, -0.3, 0.5],
[-0.2, -1.2, 0.6, 0.7],
[-0.1, -1.5, 0.3, -0.1],
[-1.4, 0.1, 1.2, -0. ]], dtype=float32), array([-0.2, 0.5, 0.5, -0.5], dtype=float32)]