189 KiB
Uczenie maszynowe
10. Sieci neuronowe – wprowadzenie
# Przydatne importy
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline10.1. Perceptron
Pierwszy perceptron liniowy
- Frank Rosenblatt, 1957
- aparat fotograficzny podłączony do 400 fotokomórek (rozdzielczość obrazu: 20 x 20)
- wagi – potencjometry aktualizowane za pomocą silniczków
Uczenie perceptronu
Cykl uczenia perceptronu Rosenblatta:
- Sfotografuj planszę z kolejnym obiektem.
- Zaobserwuj, która lampka zapaliła się na wyjściu.
- Sprawdź, czy to jest właściwa lampka.
- Wyślij sygnał „nagrody” lub „kary”.
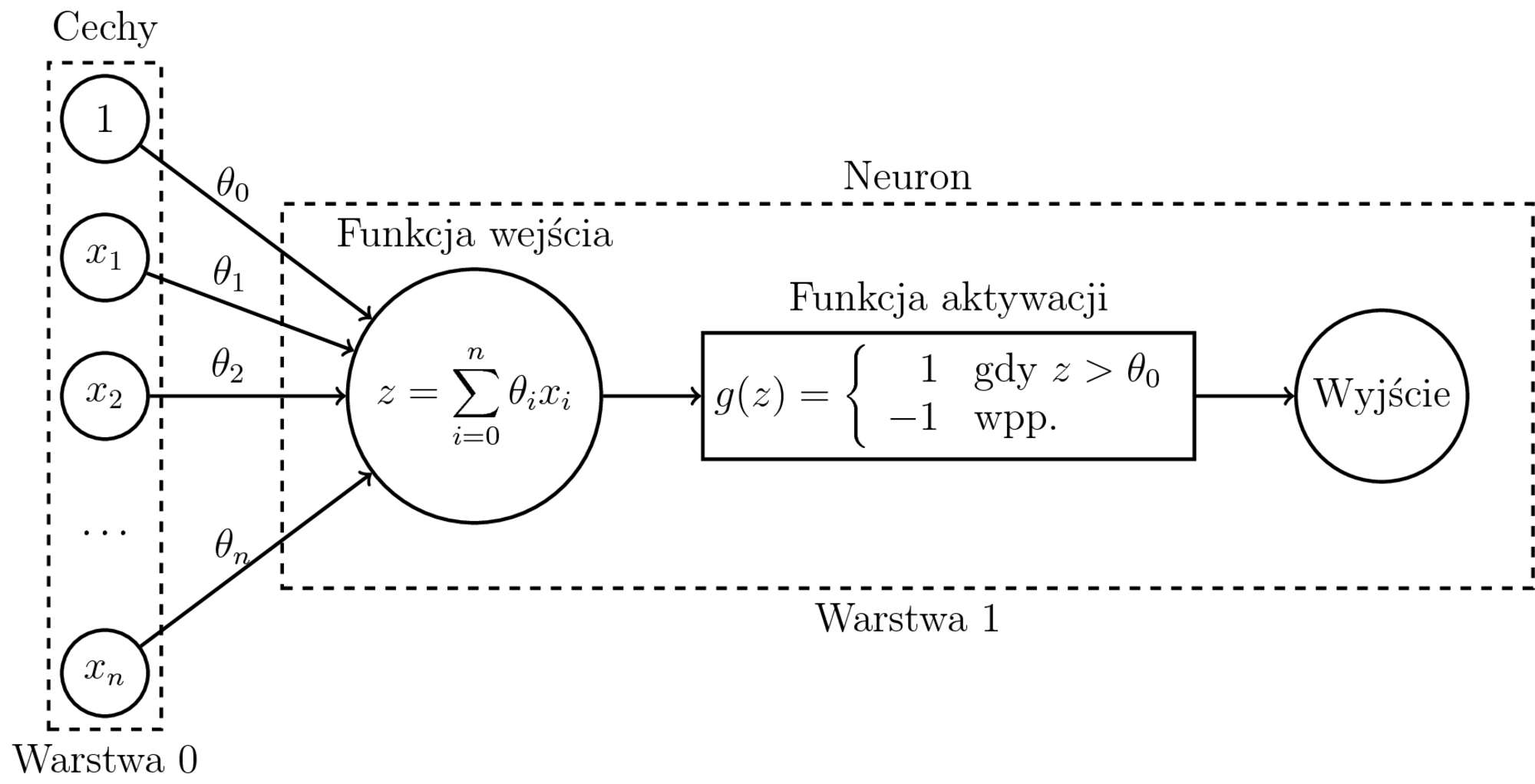
Funkcja aktywacji perceptronu
Funkcja bipolarna:
$$ g(z) = \left\{ \begin{array}{rl} 1 & \textrm{gdy $z > \theta_0$} \\ -1 & \textrm{wpp.} \end{array} \right. $$
gdzie $z = \theta_1x_1 + \ldots + \theta_nx_n$,
$\theta_0$ to próg aktywacji,
$x_0 = 1$.
def bipolar_plot():
matplotlib.rcParams.update({'font.size': 16})
plt.figure(figsize=(8,5))
x = [-1,-.23,1]
y = [-1, -1, 1]
plt.ylim(-1.2,1.2)
plt.xlim(-1.2,1.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.step(x, y, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.show()bipolar_plot()Zasada działania perceptronu
- Ustal wartości początkowe $\theta$ (wektor 0 lub liczby losowe blisko 0).
- Dla każdego przykładu $(x^{(i)}, y^{(i)})$, dla $i=1,\ldots,m$
- Oblicz wartość wyjścia $o^{(i)} = g(\theta^{T}x^{(i)}) = g(\sum_{j=0}^{n} \theta_jx_j^{(i)})$
- Wykonaj aktualizację wag (tzw. _perceptron rule): $$ \theta := \theta + \Delta \theta $$ $$ \Delta \theta = \alpha(y^{(i)}-o^{(i)})x^{(i)} $$
$$\theta_j := \theta_j + \Delta \theta_j $$
Jeżeli przykład został sklasyfikowany poprawnie:
- $y^{(i)}=1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(1 - 1)x_j^{(i)} = 0$$
- $y^{(i)}=-1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(-1 - -1)x_j^{(i)} = 0$$
Czyli: jeżeli trafiłeś, to nic nie zmieniaj.
$$\theta_j := \theta_j + \Delta \theta_j $$
Jeżeli przykład został sklasyfikowany niepoprawnie:
- $y^{(i)}=1$ oraz $o^{(i)}=-1$ : $$\Delta\theta_j = \alpha(1 - -1)x_j^{(i)} = 2 \alpha x_j^{(i)}$$
- $y^{(i)}=-1$ oraz $o^{(i)}=1$ : $$\Delta\theta_j = \alpha(-1 - 1)x_j^{(i)} = -2 \alpha x_j^{(i)}$$
Czyli: przesuń wagi w odpowiednią stronę.
Zalety perceptronu
- intuicyjny i prosty
- łatwy w implementacji
- jeżeli dane można liniowo oddzielić, algorytm jest zbieżny w skończonym czasie
Wady perceptronu
- jeżeli danych nie można oddzielić liniowo, algorytm nie jest zbieżny
def plot_perceptron():
plt.figure(figsize=(12,3))
plt.subplot(131)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.title('AND')
plt.plot([1,0,0], [0,1,0], 'ro', markersize=10)
plt.plot([1], [1], 'go', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.subplot(132)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.plot([1,0,1], [0,1,1], 'go', markersize=10)
plt.plot([0], [0], 'ro', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.title('OR')
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.subplot(133)
plt.ylim(-0.2,1.2)
plt.xlim(-0.2,1.2)
plt.title('XOR')
plt.plot([1,0], [0,1], 'go', markersize=10)
plt.plot([0,1], [0,1], 'ro', markersize=10)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('none')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('none')
ax.spines['left'].set_position(('data',0))
plt.xticks(np.arange(0, 2, 1.0))
plt.yticks(np.arange(0, 2, 1.0))
plt.show()plot_perceptron()Perceptron – funkcje aktywacji
Zamiast funkcji bipolarnej możemy zastosować funkcję sigmoidalną jako funkcję aktywacji.
def plot_activation_functions():
plt.figure(figsize=(16,7))
plt.subplot(121)
x = [-2,-.23,2]
y = [-1, -1, 1]
plt.ylim(-1.2,1.2)
plt.xlim(-2.2,2.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.step(x, y, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.subplot(122)
x2 = np.linspace(-2,2,100)
y2 = np.tanh(x2+ 0.23)
plt.ylim(-1.2,1.2)
plt.xlim(-2.2,2.2)
plt.plot([-2,2],[1,1], color='black', ls="dashed")
plt.plot([-2,2],[-1,-1], color='black', ls="dashed")
plt.plot(x2, y2, lw=3)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.annotate(r'$\theta_0$',
xy=(-.23,0), xycoords='data',
xytext=(-50, +50), textcoords='offset points', fontsize=26,
arrowprops=dict(arrowstyle="->"))
plt.show()plot_activation_functions()Uczenie regresji liniowej:
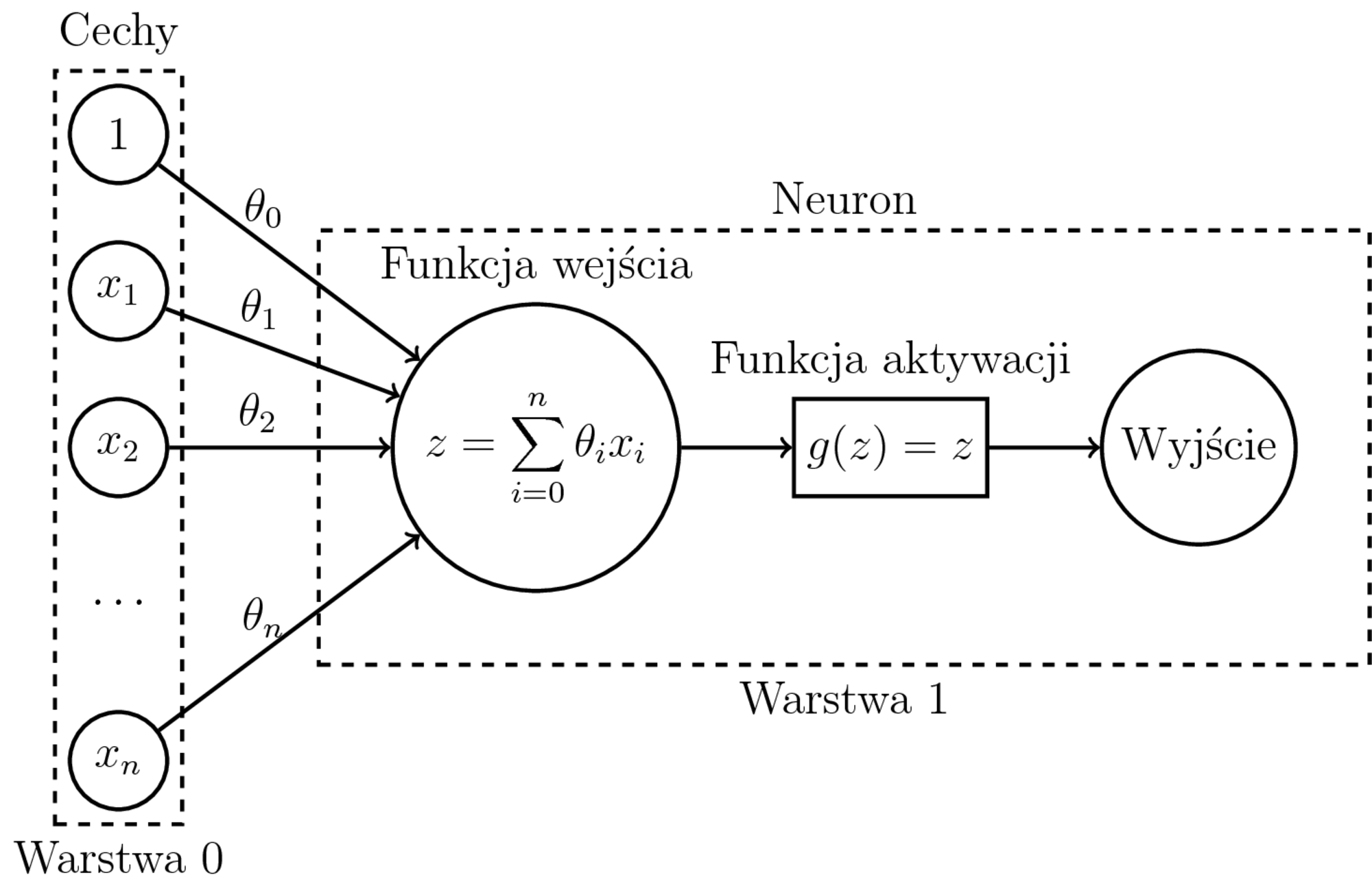
- Model: $$h_{\theta}(x) = \sum_{i=0}^n \theta_ix_i$$
- Funkcja kosztu (błąd średniokwadratowy): $$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$
- Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.
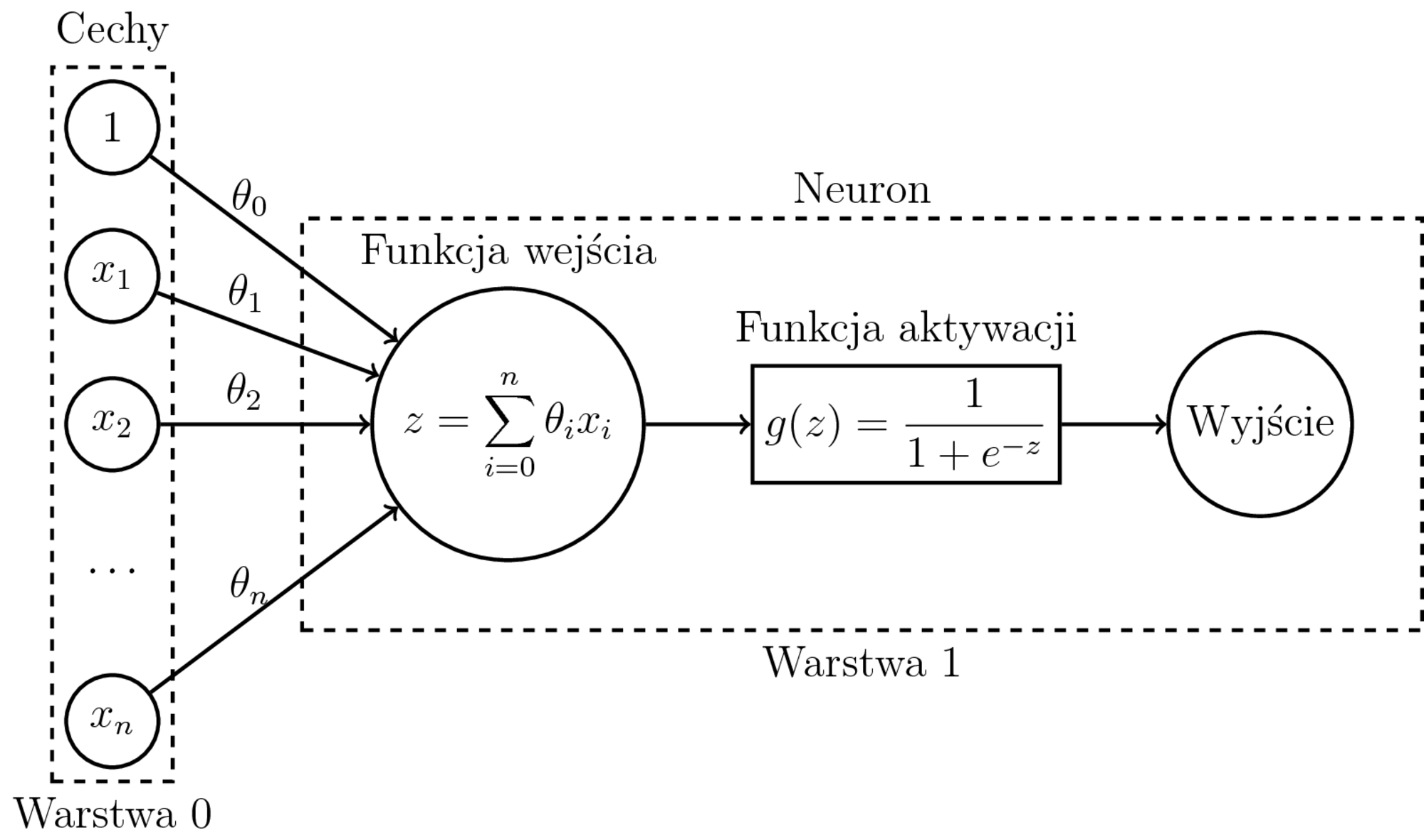
Uczenie dwuklasowej regresji logistycznej:
- Model: $h_{\theta}(x) = \sigma(\sum_{i=0}^n \theta_ix_i) = P(1|x,\theta)$
- Funkcja kosztu (entropia krzyżowa): $$\begin{eqnarray} J(\theta) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(1|x^{(i)},\theta) \\ && + (1-y^{(i)})\log(1-P(1|x^{(i)},\theta)) \big) \end{eqnarray}$$
- Po obliczeniu $\nabla J(\theta)$ - zwykły SGD.
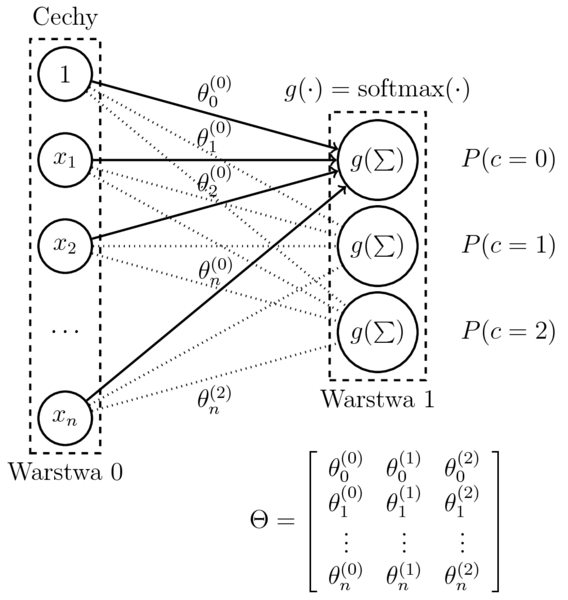
Wieloklasowa regresja logistyczna
- Model (dla $c$ klasyfikatorów binarnych): $$\begin{eqnarray} h_{(\theta^{(1)},\dots,\theta^{(c)})}(x) &=& \mathrm{softmax}(\sum_{i=0}^n \theta_{i}^{(1)}x_i, \ldots, \sum_{i=0}^n \theta_i^{(c)}x_i) \\ &=& \left[ P(k|x,\theta^{(1)},\dots,\theta^{(c)}) \right]_{k=1,\dots,c} \end{eqnarray}$$
- Funkcja kosztu (przymując model regresji binarnej): $$\begin{eqnarray} J(\theta^{(k)}) &=& -\frac{1}{m} \sum_{i=1}^{m} \big( y^{(i)}\log P(k|x^{(i)},\theta^{(k)}) \\ && + (1-y^{(i)})\log P(\neg k|x^{(i)},\theta^{(k)}) \big) \end{eqnarray}$$
- Po obliczeniu $\nabla J(\theta)$, c-krotne uruchomienie SGD, zastosowanie $\mathrm{softmax}(X)$ do niezależnie uzyskanych klasyfikatorów binarnych.
- Przyjmijmy: $$ \Theta = (\theta^{(1)},\dots,\theta^{(c)}) $$
$$h_{\Theta}(x) = \left[ P(k|x,\Theta) \right]_{k=1,\dots,c}$$
$$\delta(x,y) = \left\{\begin{array}{cl} 1 & \textrm{gdy } x=y \\ 0 & \textrm{wpp.}\end{array}\right.$$
- Wieloklasowa funkcja kosztu $J(\Theta)$ (kategorialna entropia krzyżowa): $$ J(\Theta) = -\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{c} \delta({y^{(i)},k}) \log P(k|x^{(i)},\Theta) $$
Gradient $\nabla J(\Theta)$: $$ \dfrac{\partial J(\Theta)}{\partial \Theta_{j,k}} = -\frac{1}{m}\sum_{i = 1}^{m} (\delta({y^{(i)},k}) - P(k|x^{(i)}, \Theta)) x^{(i)}_j $$
Liczymy wszystkie wagi jednym uruchomieniem SGD
Perceptron – podsumowanie
- W przypadku jednowarstowej sieci neuronowej wystarczy znać gradient funkcji kosztu.
- Wtedy liczymy tak samo jak w przypadku regresji liniowej, logistycznej, wieloklasowej logistycznej itp. (wymienione modele to szczególne przypadki jednowarstwowych sieci neuronowych).
- Regresja liniowa i binarna regresja logistyczna to jeden neuron.
- Wieloklasowa regresja logistyczna to tyle neuronów, ile klas.
Funkcja aktywacji i funkcja kosztu są dobierane do problemu.
10.2. Funkcje aktywacji
- Operacje, które każdy neuron wykonuje, to dodawanie i mnożenie. Są to funkcje liniowe.
- Złożenie funkcji liniowych jest funkcją liniową.
- Gdyby nie było funkcji aktywacji, cała sieć neuronowa działałaby jak regresja liniowa.
- Najważniejszym celem stosowania funkcji aktywacji jest wprowadzenie nieliniowości, dzięki której sieć może uczyć się zależności bardziej skomplikowanych niż tylko liniowe.
Jakie cechy powinna mieć dobra funkcja aktywacji?
- różniczkowalna (co najmniej przedziałami różniczkowalna), aby można było obliczyć jej gradient
- prosta obliczeniowo, ponieważ podczas uczenia sieci jej wartość obliczana jest wiele razy
- odporna na problem zanikającego gradientu (wyjaśnienie kilka slajdów dalej)
%matplotlib inline
import math
import matplotlib.pyplot as plt
import numpy as np
import random
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, SimpleRNN, LSTM
from keras.optimizers import Adagrad, Adam, RMSprop, SGD
from IPython.display import YouTubeVideo2023-05-04 10:23:21.183242: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: AVX2 FMA To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags. 2023-05-04 10:23:22.176521: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory 2023-05-04 10:23:22.176596: I tensorflow/compiler/xla/stream_executor/cuda/cudart_stub.cc:29] Ignore above cudart dlerror if you do not have a GPU set up on your machine. 2023-05-04 10:23:24.881062: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2023-05-04 10:23:24.881370: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2023-05-04 10:23:24.881390: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
def plot(fun):
x = np.arange(-3.0, 3.0, 0.01)
y = [fun(x_i) for x_i in x]
fig = plt.figure(figsize=(14, 7))
ax = fig.add_subplot(111)
fig.subplots_adjust(left=0.1, right=0.9, bottom=0.1, top=0.9)
ax.set_xlim(-3.0, 3.0)
ax.set_ylim(-1.5, 1.5)
ax.grid()
ax.plot(x, y)
plt.show()Funkcja logistyczna
$$ g(x) = \frac{1}{1 + e^{-x}} $$
Funkcja logistyczna – wykres
plot(lambda x: 1 / (1 + math.exp(-x)))- Funkcja logistyczna przyjmuje wartości z przedziału $(0, 1)$.
Tangens hiperboliczny
$$ g(x) = \tanh x = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} $$
Tangens hiperboliczny – wykres
plot(lambda x: math.tanh(x))- Tangens hiperboliczny przyjmuje wartości z przedziału $(-1, 1)$.
- Powstaje z funkcji logistytcznej przez przeskalowanie i przesunięcie.
- Daje szybszą zbieżność niż funkcja logistyczna dzięki temu, że przedział wartości jest symetryczny względem zera.
- Ze względu na ograniczony przedział wartości, obie funkcje (logistyczna i $\tanh$) są podatne na problem zanikającego gradientu.
Problem zanikającego gradientu (_vanishing gradient problem)
- Sigmoidalne funkcje aktywacji ograniczają wartości na wyjściach neuronów do niewielkich przedziałów ($(-1, 1)$, $(0, 1)$ itp.).
- Jeżeli sieć ma wiele warstw, to podczas propagacji wstecznej mnożymy przez siebie wiele małych wartości → obliczony gradient jest mały.
- Im więcej warstw, tym silniejszy efekt zanikania.
Sposoby na zanikający gradient
- Modyfikacja algorytmu optymalizacji (_RProp, RMSProp)
- Użycie innej funckji aktywacji (ReLU, softplus)
- Dodanie warstw _dropout
- Nowe architektury (LSTM itp.)
- Więcej danych, zwiększenie mocy obliczeniowej
ReLU (_Rectifier Linear Unit)
$$ g(x) = \max(0, x) $$
ReLU – wykres
plot(lambda x: max(0, x))ReLU – zalety
- Mniej podatna na problem zanikającego gradientu (_vanishing gradient) niż funkcje sigmoidalne, dzięki czemu SGD jest szybciej zbieżna.
- Prostsze obliczanie gradientu.
- Dzięki zerowaniu ujemnych wartości, wygasza neurony, „rozrzedzając” sieć (_sparsity), co przyspiesza obliczenia.
ReLU – wady
- Dla dużych wartości gradient może „eksplodować”.
- Za dużo „wygaszonych” neuronów może mieć negatywny wpływ na przepływ gradientu do poprzedzających warstw.
Inne funkcje aktywacji
W literaturze zaproponowano też inne funkcje aktywacji, które są lepsze od ReLU pod niektórymi względami:
- softplus
- ELU
- leaky ReLU
- SiLU / swish
W praktyce jednak ReLU pozostaje najpopularniejszą funkcją aktywacji ze względu na jej prostotę, skuteczność i szybkość obliczania.
10.3. Wielowarstwowe sieci neuronowe
czyli _Artificial Neural Networks (ANN) lub Multi-Layer Perceptrons (MLP)
Architektura sieci
- Sieć neuronowa jako graf neuronów.
- Organizacja sieci przez warstwy.
- Najczęściej stosowane są sieci jednokierunkowe i gęste.
- $n$-warstwowa sieć neuronowa ma $n+1$ warstw (nie liczymy wejścia).
- Rozmiary sieci określane poprzez liczbę neuronów lub parametrów.
Sieć neuronowa jednokierunkowa (_feedforward)
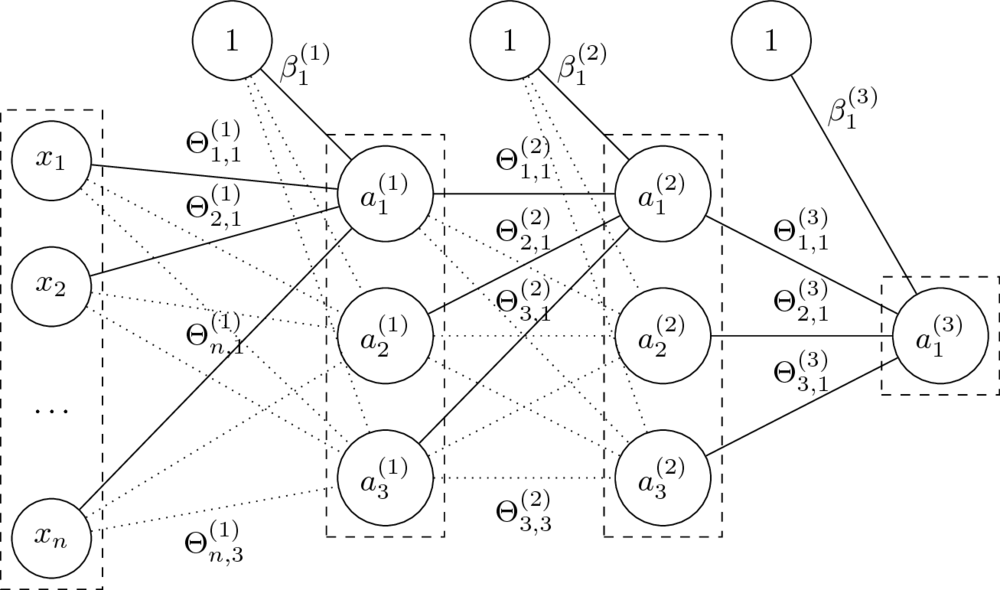
- Mając daną $n$-warstwową sieć neuronową oraz jej parametry $\Theta^{(1)}, \ldots, \Theta^{(L)} $ oraz $\beta^{(1)}, \ldots, \beta^{(L)} $, liczymy:
$$a^{(l)} = g^{(l)}\left( a^{(l-1)} \Theta^{(l)} + \beta^{(l)} \right). $$
- Funkcje $g^{(l)}$ to tzw. funkcje aktywacji.
Dla $i = 0$ przyjmujemy $a^{(0)} = \mathrm{x}$ (wektor wierszowy cech) oraz $g^{(0)}(x) = x$ (identyczność).
- Parametry $\Theta$ to wagi na połączeniach miedzy neuronami dwóch warstw.
Rozmiar macierzy $\Theta^{(l)}$, czyli macierzy wag na połączeniach warstw $a^{(l-1)}$ i $a^{(l)}$, to $\dim(a^{(l-1)}) \times \dim(a^{(l)})$.
- Parametry $\beta$ zastępują tutaj dodawanie kolumny z jedynkami do macierzy cech.
Macierz $\beta^{(l)}$ ma rozmiar równy liczbie neuronów w odpowiedniej warstwie, czyli $1 \times \dim(a^{(l)})$.
- Klasyfikacja: dla ostatniej warstwy $L$ (o rozmiarze równym liczbie klas) przyjmuje się $g^{(L)}(x) = \mathop{\mathrm{softmax}}(x)$.
- Regresja: pojedynczy neuron wyjściowy jak na obrazku. Funkcją aktywacji może wtedy być np. funkcja identycznościowa.
- Pozostałe funkcje aktywacji najcześciej mają postać sigmoidy, np. sigmoidalna, tangens hiperboliczny.
- Mogą mieć też inny kształt, np. ReLU, leaky ReLU, maxout.
Uczenie wielowarstwowych sieci neuronowych
Mając algorytm SGD oraz gradienty wszystkich wag, moglibyśmy trenować każdą sieć.
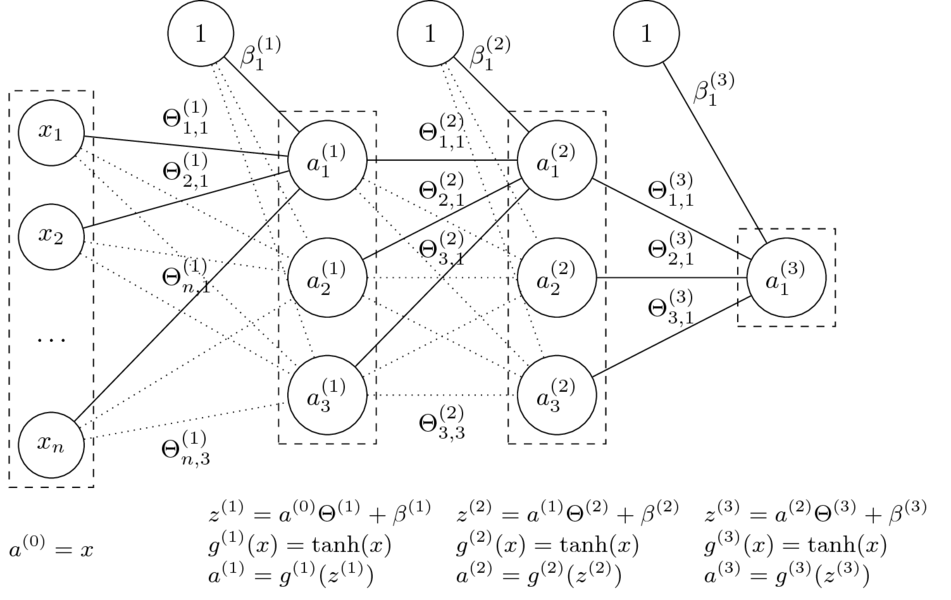
Niech: $$\Theta = (\Theta^{(1)},\Theta^{(2)},\Theta^{(3)},\beta^{(1)},\beta^{(2)},\beta^{(3)})$$
Funkcja sieci neuronowej z grafiki:
$$\small h_\Theta(x) = \tanh(\tanh(\tanh(x\Theta^{(1)}+\beta^{(1)})\Theta^{(2)} + \beta^{(2)})\Theta^{(3)} + \beta^{(3)})$$
- Funkcja kosztu dla regresji: $$J(\Theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h_\Theta(x^{(i)})- y^{(i)})^2 $$
Jak obliczymy gradienty?
$$\nabla_{\Theta^{(l)}} J(\Theta) = ? \quad \nabla_{\beta^{(l)}} J(\Theta) = ?$$
- Postać funkcji kosztu zależna od wybranej architektury sieci oraz funkcji aktywacji.
$$\small J(\Theta) = \frac{1}{2}(a^{(L)} - y)^2 $$ $$\small \dfrac{\partial}{\partial a^{(L)}} J(\Theta) = a^{(L)} - y$$
$$\small \tanh^{\prime}(x) = 1 - \tanh^2(x)$$