grafika-uam-rybki-21-22/cw 4/cw4.md

### 0. (Jeżeli nie zrobiłeś poprzednich zadań związanych z shaderami)
 Obejrzyj pliki shader_4_1.vert i shader_4_1.frag. Zwróć uwagę w szczególności na zmienna interpNormal, przy uzyciu ktorej wektory normalne wierzchołków dostępne w vertex shaderze przesyłane są do fragment shadera. Pliki shader_4_2.vert i shader_4_2.frag na razie nie będą wykorzystywane

### 1. Oblicz we fragment shaderze oświetlenie obiektu przy użyciu modelu Phonga dla światła rozproszonego (`diffuse`):

a) Przekaż źródło światła. Na razie przyjmiemy kierunkowy model oświetlenia, dlatego źródło będzie opisane jako wektor kierunkowy:

- Prześlij do *fragment shadera* zmienna typu `uniform vec3` (nazwij ją np. `lightDir`), w której będzie się znajdować wektor kierunkowy:

- Należy to zrobić podobnie do tego, jak przesyłana jest zmienna `objectColor`. Jedyna różnica będzie taka, ze kierunek padania światła nie zależy od obiektu, wiec wywołanie `glUniform3f` powinno pojawić się tylko raz, przed rysowaniem wszystkich obiektów.

- Jako kierunek światła wybierz dowolny wektor jednostkowy. (Możesz wziąć dowolny niezerowy wektor następnie go znormalizować)


b) Oblicz natężenie:

- znormalizuj wektor normalny przed użyciem go w obliczeniach (uśrednianie wektorów normalnych wierzchołków może spowodować, ze przestaje one być jednostkowe).

- Natężenie to iloczyn skalarny wektora normalnego powierzchni i odwrotnego wektora kierunku padania światła. Skorzystaj z funkcji `dot`.

- Natężenie nie może być ujemne. Przytnij natężenie do zera przy użyciu: `x = max(x, 0.0)`

c) Zastosuj obliczone natężenie aby zmodyfikować kolor obiektu:

- Przemnóż kolor RGB piksela przez obliczone natężenie.

### 2. Dlaczego oświetlenie statku nie zmienia się podczas jego obracania?

(Wektory normalne są w układzie lokalnym modelu, a wektor padania światła w układzie świata)

Należy wykonać transformacje wektorów normalnych do przestrzeni świata:

- Prześlij macierz modelu rysowanego obiektu (*model Matrix*) jako osobna zmienna do *vertex shadera* (`uniform mat4`).

- Przemnóż przez te macierz wektor normalny wierzchołka przed przeslaniem go do *fragment shadera*.

- Współrzędna **w** dopisana do wektora przed mnożeniem przez macierz powinna być ustawiona na 0. Wynika to z tego, ze w przypadku transformacji wektorów reprezentujących kierunki w przestrzeni, nie chcemy dokonywać translacji - np. wektor normalny do powierzchni zależy od orientacji obiektu, ale nie od jego pozycji (przesunięcia) w przestrzeni świata.

### 3. Uzupełnił model o czynnik światła odbitego (`specular`). W tym celu:

a) Potrzebny będzie wektor od rysowanego fragmentu do pozycji kamery:

- Wyślij pozycje kamery (`cameraPos`) jako kolejna zmienna do *fragment shadera*.

- Podobnie jak wektory normalne prześlij z *vertex* do *fragment shadera* pozycje wierzchołków (`vertexPosition`) w przestrzeni świata (czyli pomnożone przez macierz *modelMatrix*). Pamiętaj, ze tym razem wektory reprezentują punkty, a nie kierunki - współrzędna **w** przed mnożeniem musi być ustawiona na 1. W wyniku rasteryzacji otrzymamy w shaderze fragmentu jego pozycję (nazywaną pozycją fragmentu)

- Oblicz wektor **V** jako znormalizowaną różnice pozycji kamery i pozycji fragmentu.

b) Oblicz natężenie światła odbitego we *fragment shaderze*:

- Oblicz wektor kierunku odbicia światła **R** przy użyciu funkcji [`reflect`](https://www.khronos.org/registry/OpenGL-Refpages/gl4/html/reflect.xhtml). Pamiętaj, żeby przesłać do funkcji odwrócony wektor kierunku światła. 

- Oblicz natężenie: iloczyn skalarny **V** i **R**, przycięty do zera ( `max(...,0.0)` ), a następnie podniesiony do wysokiej potęgi (np. 8, 50, 1000), która jest miara połyskliwości powierzchni

c) Ustal ostateczny kolor piksela na  `objectColor * diffuse + vec3(1.0) * specular`. Oznacza to najprostszy przypadek, gdy kolor światła odbitego jest biały.

### 4. Stwórz układ planetarny - jedna nieruchoma kule na środku (Słonce) i kilka orbitujących wokół niej planet.
Niech przynajmniej jedna planeta ma księżyce.

### 5. W układzie planetarnym obiektem oświetlającym powinno być słońce, dlatego zamień oświetlenie kierunkowe na punktowe:

- Zamiast przesyłać (w `lightDir`) kierunek światła, prześlij pozycję słońca (taką jak ustawiłeś w punkcie powyżej) jako uniform vec3 (nazwij go `lightPos`).

- Oblicz kierunek światła odejmując od pozycji fragmentu pozycję światła i normalizując ją. Zapisz wynik w zmiennej `lightDir`.

- Słońce będzie czarne, nie martw się tym, tylko spójrz na punkt następny


###  6. Źródło światła znajduje się wewnątrz kuli, która reprezentuje słońce, dlatego jest czarna. By to naprawić napisz osobny shader, który będzie odpowiadać za renderowanie słońca.
a) zainicjalizuj shader:
- Pliki **shader_4_2.vert**_ i **shader_4_2.frag** są identyczne jak **4_1** na przed zmianami, będą punktem wyjścia dla *shadera* słońca.

- Utwórz zmienną globalną `GLuint programSun` na shader słońca. Załaduj do niej powyższe shadery w funkcji init. (skorzystaj z `shaderLoader.CreateProgram`).


b) zmień shader dla słońca: 
- funkcja `drawObject` korzysta z globalnej zmiennej `program` jako shader. Zmodyfikuj funkcję tak, żeby shader był jej argumentem.
- dodaj odpowiedni shader w wywołaniach `drawObject`

- Musisz zmienić shader na `programSun` na czas rysowania słońca przy użyciu funkcji `glUseProgram.` Pamiętaj, żeby nie rysować tym shaderem innych obiektów. (Najprościej będzie rysować słońce po wszystkich innych obiektach).

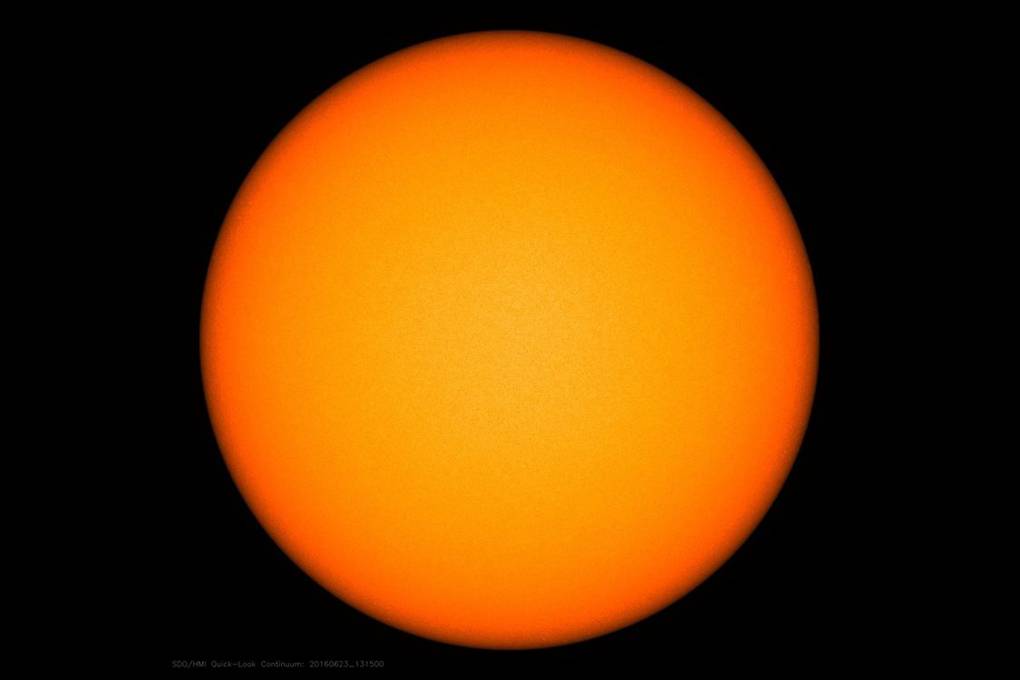
### 7.* Zmień shader słońca na bardziej realistyczny.
Na poniższym obrazku jest zdjęcie słońca. jest ono ciemniejsze na brzegach spróbuj uzyskać podobny efekt. Przydadzą się wektory z poprzednich punktów, jak wektor normalny i wektor **V**.

![](https://wi-images.condecdn.net/image/DEGypMQdE59/crop/1020/f/sunmeta.jpg)