GRK/cw 7/zadanie_2.md

Interpolacja kwaternionów

Celem tego zadania jest przećwiczenie interpolacji obrotów przy użyciu kwaternionów.

Opis projektu

Plik main7 rysuje futurystyczne miasto i latające samochody, które startują z jednego wieżowca, okrążają miasto i lądują na drugim. Jeżeli rysowanie miasta jest zbyt wymagające dla komputera, to w funkcji initModels można podmienić model na mniej złożony, zmniejszenie wartości dla multisamplingu też powinno poprawić wydajność (linijka glutSetOption(GLUT_MULTISAMPLE, 4);). Do ładowania obiektów jest wykorzystywana biblioteka Assimp z prostą obsługą materiałów.

Statki poruszają się po krzywej wyznaczonej przez punkty kontrolne zapisane w keyPoints i interpolowane liniowo. Nie mają one zdefiniowanych obrotów, zadaniem jest wyliczenie im obrotów.

Dla łatwiejszego debugowania kamera została rozwinięta o następujące opcje:

• obroty przy pomocy kwaternionów
• przyciski q i e przenoszą kamerę w okolicę następnego/poprzedniego punktu kontrolnego
• przycisk 0 przenosi do pierwszego punktu kontrolnego
• przycisk 1 przyczepia kamerę do statku.

Materiały i graf sceny

Import

modele które importujemy w trakcie tych zajęć mają rozszerzenie fbx są to dużo bardziej skomplikowane pliki, mogą one zawierać więcej niż jeden mesh lokalne macierze transformacji i informację o materiałach.

Materiały

Do tej pory ręcznie wybieraliśmy program, którym rysowaliśmy. wiązało się to z tym, że trzeba było pamiętać jakie parametry należy przesłać do danego obiektu. Rozwiązaniem jest przechowywanie w materiałach. W projekcie w klasie RenderContext jest wskaźnik na zmienną typu Material, której zadaniem jest przechowywanie tej informacji.

Graf sceny

Sceny w bardziej złożonych projektach potrafią być skomplikowane. Obiekty w scenie są umieszczane hierarchicznie. przykładowo bohater posiada ręce, które poruszają się razem z nim (z reguły) jednak mogą same z siebie się poruszać, gdy postać atakuje. w ręku tej postaci może znajdować się miecz lub inna broń i ta broń będzie poruszać zawsze gdy bohater się się będzie przemieszczać, ale też gdy się zamachnie. W poprzednich projektach przykładem takich zależności była planeta i krążący wokół niej księżyc. Takich zależności może być więcej i pamiętanie wszystkich poprzednich interakcji staje się kłopotliwe. Rozwiązaniem, które pozwala wprowadzić taką hierarchię jest graf sceny. Graf sceny jest drzewem, w którym każdy węzeł jest jakimś obiektem w grze oraz zawiera informację o lokalnej transformacji względem obiektu nadrzędnego-ojca. To rozwiązanie pozwala myśleć tylko o lokalnych transformacjach, a globalne pobrać z nadrzędnych węzłów.

W naszym projekcie graf sceny jest zrealizowany w formie tablicy. To znaczy w projekcie znajdują się 2 tablice city i car. Odpowiadają one za grafy dla miasta i pojazdu, jak nazwa wskazuje. Tablice zawierają struktury Core::Node:

	struct Node {
		std::vector<RenderContext> renderContexts;
		glm::mat4 matrix;
		int parent;
	};

Zawiera ona RenderContexty, które składają się na ten obiekt, macierz transformacji oraz indeks obiektu nadrzędnego, czyli np dla car[3] jego ojcem będzie car[car[3].parent], jeżeli atrybut parent jest równy -1 to znaczy, że dotarliśmy do korzenia, czyli obiektu który już nie ma nadrzędnego.

Zadanie

Prześledź jak ładowane są obiekty w funkcji initModels().

W tej chwili nic się nie wyświetla. Jak wciśniesz r to kamera zostanie przeniesiona do centrum, gdzie znajdują się wszystkie obiekty. Wynika to z tego, że funkcjarenderRecursive jest niekompletna. Dopisz obliczanie macierzy transformacji. Najpierw przypisz do niej macierz transformacji z obecnego węzła node, następnie w pętli domnóż od lewej macierz transformacji nadrzędnego węzła, nadrzędnego nadrzędnego węzła i tak aż do korzenia. Po wykonaniu powinna pojawić scena, która zwiera miasto i latające statki. W następnych zadaniach skupimy się na poprawieniu ich zachowania.

Interpolacja

Większość pracy będzie się dziać w funkcji animationMatrix, ma ona zmienną speed, która może być pomocna przy debugowaniu.

Interpolacja krzywej

W tej punkty kontrolne są interpolowane liniowo w funkcji animationMatrix. Funkcja ta oblicza na podstawie otrzymanego czasu oblicza macierz transformacji obiektu (statku) poruszającego się po krzywej. Oblicza ona pomiędzy jakimi puntami powinien znajdować się obiekt (zmienna i) oraz parametr t który określa jaki punkt pomiędzy punktami kontrolnymi i oraz i+1wybrać. Zastąp interpolację liniową na Catmull-Roma w linii:

	glm::vec3 pos = (keyPoints[std::max(0, index)] * t + keyPoints[std::min(size, index + 1)] * (1 - t));

Użyj funkcji glm::catmullRom(). Przyjmuje ona cztery argumenty typu glm::vec3 (v1, v2, v3, v4) i jeden argument typu float (s). Zwraca ona glm::vec3, w którym znajduje się zinterpolowana pozycja między punktami v2 i v3 (parametr s wybiera punkt na ścieżce; dla s=0 zwracane jest v2, dla s=1 zwracane jest v3, dla 0<s<1 zwracana jest zinterpolowana pozycja na ścieżce). Punkty v1 i v4 są dodatkowymi punktami kontrolującymi krzywiznę ścieżki. Dla krzywych Catmulla-Roma, należy jako v1,v2,v3,v4 podać po prostu cztery kolejne punkty ze zbioru punktów kontrolnych

Interpolacja kwaternionów

Celem tego zadania jest przećwiczenie interpolacji obrotów przy użyciu kwaternionów.

Obliczenie kierunków

W pierwszej kolejności potrzebujemy obliczyć kwaterniony odpowiadające obrotom statków między kolejnymi punktami kontrolnymi. Chcemy, żeby statek był skierowany w kierunku lotu. Najpierw musimy uzyskać znormalizowany wektor kierunkowy dla każdej pary 2 kolejnych punktów kontrolnych jak na rysunku poniżej.

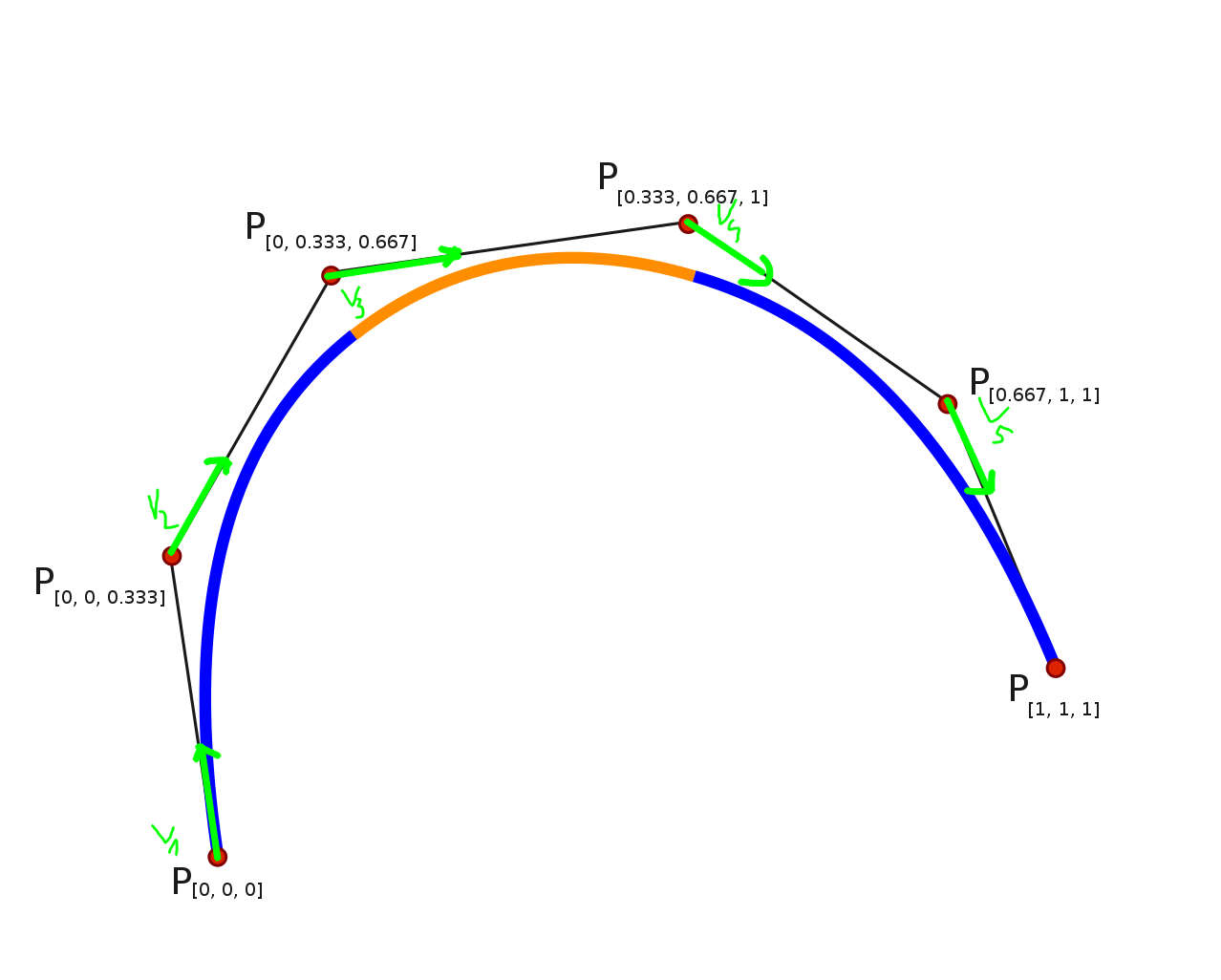Nastęnie należy obliczyć kwaterniony odpowiadające za obrót z początkowej orientacji statku (opisywanej przez wektor (0,0,1)) do orientaci wyznaczonej przez wektory kietunkowe. Żeby obliczyć obrót między jednym wektorem a drugim, należy obliczyć oś obrotu, oblicza się go za pomocą iloczynu wektorowego, oraz kąt obrotu, oblicza się za pomocą iloczynu skalarnego. Może być kuszące policzenie wektora obrotu pomiędzy początkowym wektorem kierunkowym a kolejnymi wektorami, ale takie rozwiązanie może prowadzić do niepożądanych zachowań. Dlatego należy obliczać obroty pomiędzy kolejnymi wektorami i je akumulować.

Zadanie

Uzupełnij funkcję initKeyRoation o wypełnienie std::vector<glm::quat> keyRotation kwaternionami.

1. Zainicjalizuj zmienną glm::vec3 oldDirection wektorem o współrzędnych (0,0,1), czyli początkowej orientacji pojazdu
2. Zainicjalizuj zmienną glm::quat oldRotationCamera kwaternionem identycznościom (1,0,0,0).
3. W pętli for po i od 0 do liczba keyPoints odjąć 1.
   1. Oblicz nowy kierunek: odejmij od punktu końcowego: keyPoints[i+1] punkt początkowy: keyPoints[i].
   2. Oblicz nową rotację, skorzystaj z funkcji glm::rotationCamera przemnóż jej wynik przez oldRotationCamera od prawej i całość znormalizuj.
   3. Dodaj nowy obrót do keyRotation.
   4. Podmień oldDritection na nowy kierunek i oldRotationCamera na nowy obrót.
4. Po wszystkim kwaternionów jest o jeden mniej niż punktów dodaj jeszcze jeden o wartościach (1,0,0,0) na koniec.

Interpolacja

Do interpolacji użyjemy funkcji slerp opisanej wzorem

 slerp(\hat{q}_i,\hat{q}_{i+1},t) = \frac{\sin(\phi(1-t))}{\sin(\phi)}\hat{q}_i+\frac{\sin(\phi t)}{\sin(\phi)}\hat{q}_{i+1}

gdzie \hat{q_i},\hat{q}_{i+1} są interpolowanymi kwaternionami, t jest parametrem od 0 do 1, natomiast \phi można otrzymać z wzoru cos\phi = q_xr_x+q_yr_y+q_zr_z+q_wr_w. dla t\in\left[0,1\right] slerp oblicza najkrótszą ścieżkę pomiędzy kwaternionami p i q w przestrzeni kwaternionów jednostkowych. Nie będziemy jej obliczać samodzielnie, skorzystamy z implementacji glm::slerp.

W funkcji animationMatrix dodaj interpolację kwaternionów

glm::mat4 animationMatrix(float time) {
    ...
	//index of first keyPoint
	int index = 0;

	while (distances[index] <= time) {
		time = time - distances[index];
		index += 1;
	}

	//t coefitient between 0 and 1 for interpolation
	float t = time / distances[index];
    ...
	//implement corect animation
	auto animationRotation = glm::quat(1,0,0,0);

	glm::mat4 result = glm::translate(pos) * glm::mat4_cast(animationRotation);


	return result;

}

Pobierz z keyRotation kwaterniony o indeksach index i index+1 wywołaj glm::slerp z nimi jako argumentami. Trzecim parametrem powinna być wartość t.

Uwaga! pobierając wartości z wektora keyRotation pamiętaj, żeby nie wyjść poza jego zakres, najlepiej weż maksimum z indeksu i zera oraz minimum z indeksu i rozmiaru wektora.

Otrzymana animacja będzie ciągła, ale w punktach kontrolnych będzie widoczne szarpnięcie wywołane przez to, że funkcja slerp nie jest gładka, gdy przechodzimy do kolejnej pary kwaternionów. By zniwelować ten efekt użyjemy funkcji glm::squat.

Funkcja squat podobnie jak Catmull-Rom przyjmuje 4 wartości jednak zamiast przyjmować 4 kolejne wektory, przyjmuje 2 kwaterniony interpolowane i 2 kwaterniony pośrednie. opisana jes t wzorem:

squad(\hat{q}_{i},\hat{q}_{i+1},\hat{a}_{i},\hat{a}_{i+1},t)=slerp(slerp(\hat{q}_{i},\hat{q}_{i+1},t),slerp(\hat{a}_{i},\hat{a}_{i+1},t),2t(1-t))

gdzie \hat{q}_{i},\hat{q}_{i+1} to interpolowane kwaterniony, t to parametr od 0 do 1. Natomiast \hat{a}_{i},\hat{a}_{i+1} są opisane wzorem:

\hat{a}_i = \hat{q}_i\exp\left[-\frac{\log(\hat{q}_i^{-1}\hat{q}_{i-1})+\log(\hat{q}_i^{-1}\hat{q}_{i+1})}{4}\right].

Zadanie

Zamień interpolację kwaternionów ze slerp na squat. Po pierwsze pobierz wartości \hat{q}_{i-1}, \hat{q}_{i}, \hat{q}_{i+2}, \hat{q}_{i+2} z keyRotation (i odpowiada zmiennej index jak poprzednio), oblicz \hat{a}_i, \hat{a}_{i+1}, funkcje, które będą potrzebne to glm::inverse, glm::exp, glm::log. Na koniec podmień slerp na squat.

Teraz przejścia między obrotami powinny być gładkie. Jedna rzecz, która pozostaje, to poprawić moment lądowania. Ustaw ręcznie kilka ostatnich kwaternionów tak, żeby statek lądował poziomo.