xcjajx/Rachunek_prawdopodobienstwa

Fork 0

xcjajx 2c99b7f277 Upload files to "Przewodnik_studenta_lab"

2024-10-03 07:46:39 +02:00

185 KiB

Raw Permalink Blame History

Bardzo krótkie wprowadzenie do programu R

Podstawowe informacje

R - język programowania / pakiet statystyczny.
Jest to język darmowy, rozpowszechniany na licencji GNU General Public License (GPL).
Jest przydatny szczególnie dla osób zainteresowanych statystyką/analizą danych.
R zawiera ponad 10000 pakietów do różnych zastosowań.
Program R można pobrać z następującej strony.

RStudio

R studio - edytor do programu R, ułatwiający pracę z tym programem.
dystrybuowany na licencji AGPL v3.
w RStudio można też wykonywać kody napisane w Pythonie.
RStudio można pobrać z następującej strony.
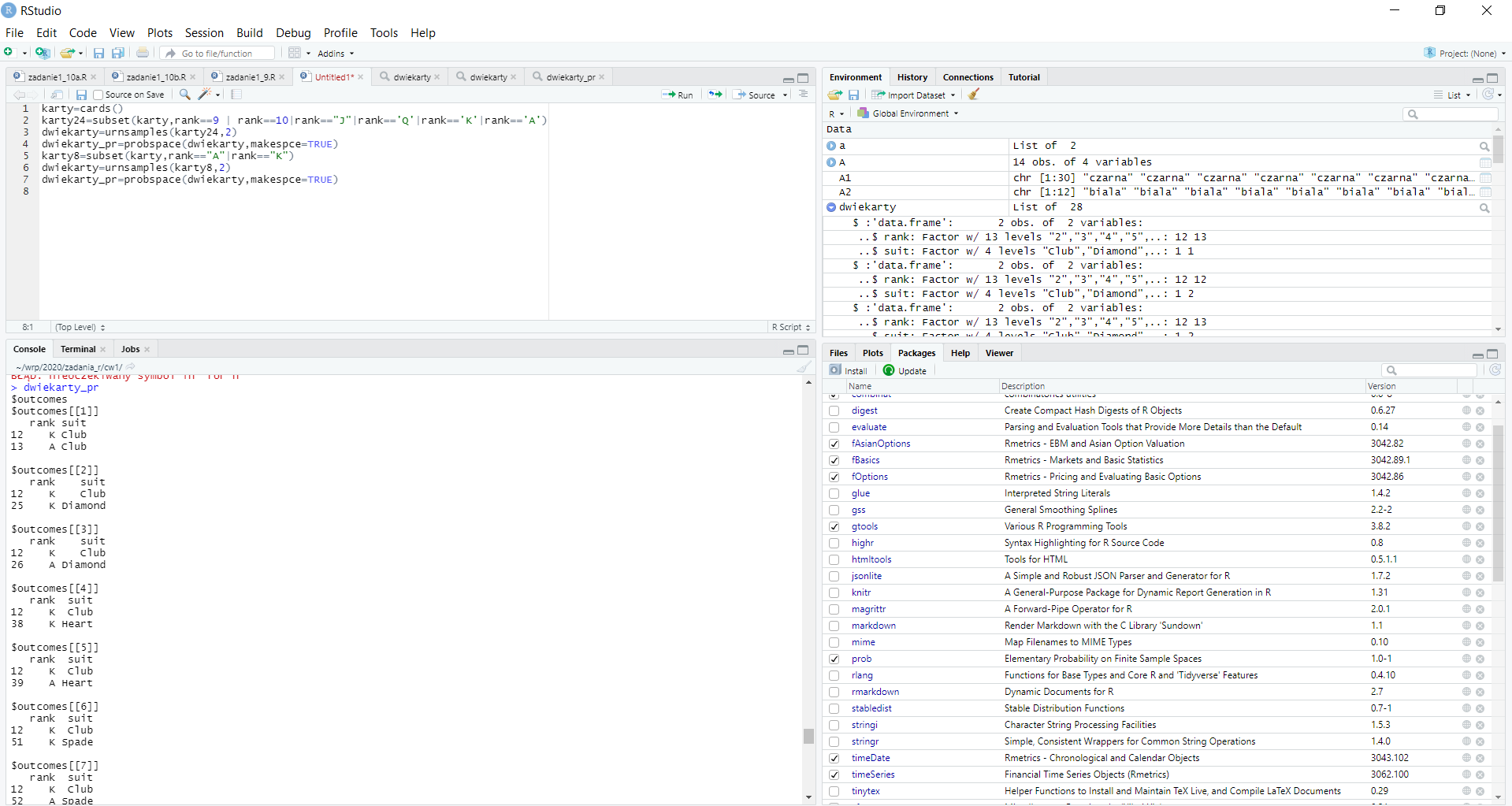
Przykładowy wygląd paneli Rstudio zaprezentowany jest poniżej.

Pakiety

Aby w pełni korzystać z możliwości R, będziemy wykorzystywać różne gotowe pakiety.

Do instalacji pakietu używamy polecenia install.packages().
Do załadowania pakietu używamy polecenia library().
Jeśli używamy RStudio możemy wyświetlić listę zainstalowanych i załadowanych pakietów (na wcześniej zaprezentowanym rysunku znajduje się ona w prawym dolnym rogu - załadowane pakiety oznaczone są haczykiem). Ponadto, możemy też ładować pakiety klikając na kwadraciki znajdujące się na tej liście przy nazwie odpowiedniego pakietu.

Uwaga: Nie wszystkie pakiety są dostępne w wersji online Jupytera. W związku z tym poniższy i kolejne przykłady mogą wymagać przekopiowania instrukcji do RStudio.

install.packages("gtools")
library("gtools")

Installing package into ‘/usr/local/lib/R/site-library’
(as ‘lib’ is unspecified)

Warning message in install.packages("gtools"):
“'lib = "/usr/local/lib/R/site-library"' is not writable”

Error in install.packages("gtools"): unable to install packages
Traceback:

1. install.packages("gtools")
2. stop("unable to install packages")

Wektory i macierze

Jednym z podstawowych obiektów, które będą nas interesowały w kontekście naszych zajęć są wektory i macierze.

Definiowanie wektorów

Poniżej przedstawimy kilka podstawowych sposobów definiowania wektorów wraz z przykładami.

Wektory możemy przypisać do zmiennej używając jednego z operatorów: =, <-, ->.
Podstawową funkcją służącą do definiowania wektorów jest c(), gdzie w nawiasach wpisujemy kolejne elementy wektora.

a = c(1, 2, -4)
b = c('as', 'krol', 'dama')

1
2
-4

'as'
'krol'
'dama'

Polecenie i:j, gdzie $i,j$ to liczby całkowite, tworzy ciąg arytmetyczny o pierwszym elemencie równym $i$ oraz różnicy równej $1$ (jeśli $j>i$) lub $-1$ (jeśli $j<i$), którego ostatni wyraz nie przekracza $j$.
Polecenie seq(from=i,to=j,by=r), gdzie $i,j,r$ to liczby całkowite, tworzy ciąg arytmetyczny o pierwszym elemencie równym $i$ oraz różnicy równej $r$, którego ostatni wyraz nie przekracza $j$.

c = 2:9
d = 9:2
e = seq(2, 9, 3)
f = seq(10, 1, -1.5)

Polecenie rep(x,...) pozwala tworzyć wektory, w których elementy się powtarzają. W tym wypadku x jest wektorem elementów, które mają się powtórzyć, a w miejsce kropek wpisujemy informację o tym, ile razy mają się powtórzyć elementy (jeśli wpiszemy tu liczbę $n$, to cały wektor zostanie powtórzony $n$ razy, a jeśli podamy wektor liczb v o tej samej długości, co x, to każdy element wektora x zostanie powtórzony tyle razy, ile wskazuje na to odpowiednia współrzędna wektora v).

g = rep(c('as', 'krol'), 2)
h = rep(c('as', 'krol'), c(2, 3))

'as'
'krol'
'as'
'krol'

'as'
'as'
'krol'
'krol'
'krol'

Istnieje kilka wbudowanych, przydatnych wektorów, np.:
- letters: wektor zawierajacy $26$-literowy alfabet (małe litery);
- LETTERS: wektor zawierajacy $26$-literowy alfabet (duże litery);
- month.name: wektor zawierający nazwy miesięcy (po angielsku).

letters

LETTERS

month.name

'January'
'February'
'March'
'April'
'May'
'June'
'July'
'August'
'September'
'October'
'November'
'December'

Definiowanie macierzy

Pokażemy teraz, jak możemy definiować macierze.

Podstawowym poleceniem do generowania macierzy jest matrix(v, nrow=n, ncol=m, byrow=FALSE), gdzie v jest wektorem danych do wpisania do macierzy, nrow i ncol oznaczają odpowiednio liczbę wierszy i kolumn w macierzy, a byrow zawiera informację o tym, w jaki sposób elementy wektora v mają być wpisywane do macierzy. Jeśli byrow ma wartość TRUE, to kolejne elementy będą wpisywane w kolejne wiersze macierzy, w przeciwnym przypadku będą wpisywane w kolejnych kolumnach. Nie jest konieczne podawanie zarówno liczby wierszy, jak i kolumn - jeśli podamy tylko jeden wymiar, drugi zostanie wybrany automatycznie tak, aby do macierzy można było wpisać wszystkie elementy wektora v. Jeśli iloczyn liczb $n$ i $m$ jest większy niż długość wektora v, to w brakujące miejsca są ponownie wstawiane elementy początkowe wektora v. Jeśli natomiast ten iloczyn będzie mniejszy od długości wektora v, to do macierzy zostaną wpisane tylko początkowe elementy wektora, a pozostałe zostaną zignorowane. W obu przypadkach zostanie wyświetlone ostrzeżenie o braku kompatybilności wymiarów.

# Definiujemy macierze, których elementami są nazwy miesięcy
m = month.name

# Zwróćmy uwagę, że w macierzy M1 nazwy miesięcy wpisywane są kolejno wierszami
M1 = matrix(m, nrow=3, ncol=4, byrow=TRUE)
# Natomiast w macierzy M2 nazwy wpisywane są kolejno kolumnami
M2 = matrix(m, nrow=3, ncol=4, byrow=FALSE)

# W macierzy M3 liczba wierszy nie jest dzielnikiem długości wektora m, więc niektóre elementy tego wektora zostaną wykorzystane wielokrotnie
M3 = matrix(m, nrow=5)
# Liczba elementów macierzy M4 jest mniejsza od długości wektora m, więc jego końcowe elementy nie zostaną wykorzystane
M4 = matrix(m, nrow=2, ncol=3)

Warning message in matrix(m, nrow = 5):
“data length [12] is not a sub-multiple or multiple of the number of rows [5]”
Warning message in matrix(m, nrow = 2, ncol = 3):
“data length differs from size of matrix: [12 != 2 x 3]”

M1

A matrix: 3 × 4 of type chr
January	February	March	April
May	June	July	August
September	October	November	December

M2

A matrix: 3 × 4 of type chr
January	April	July	October
February	May	August	November
March	June	September	December

M3

A matrix: 5 × 3 of type chr
January	June	November
February	July	December
March	August	January
April	September	February
May	October	March

M4

A matrix: 2 × 3 of type chr
January	March	May
February	April	June

Jeśli mamy dany wektor v o długości $k$, to możemy zamienić go na macierz dwuwymiarową o wymiarach $n\times m$ (gdzie $k=n\cdot m$), używając polecenia dim(v)=c(n,m). Wówczas elementy wektora v zostaną wpisane kolejno kolumnami do macierzy.
Jeśli mamy dany ciąg wektorów/macierzy, to możemy je połączyć w większy obiekt używając poleceń rbind (obiekty będą łaczone wierszowo, tzn. kolejne wektory/macierze będą wpisywane w kolejne wiersze tworzonej tabeli) lub cbind (obiekty będą łączone kolumnowo, tzn. kolejne wektory/macierze będą wpisywane w kolejne kolumny tworzonej tabeli).

dim(c) = c(4,2)
c

A matrix: 4 × 2 of type int
2	6
3	7
4	8
5	9

A = rbind(a, e)
A

A matrix: 2 × 3 of type dbl
a	1	2	-4
e	2	5	8

B = cbind(a, e)
B

A matrix: 3 × 2 of type dbl
a	e
1	2
2	5
-4	8

Odwoływanie się do elementów wektora / macierzy

Pokażemy teraz, w jaki sposób możemy odwoływać się do elementów danego wektora v

v[i] - $i$-ty element wektora v (wektory indeksowane są od $1$);
v[x], gdzie x jest wektorem indeksów zwraca elementy wektora v o indeksach podanych w wektorze x;
v[-i] - wszystkie elementy wektora v poza $i$-tym;
v[-x], gdzie x jest wektorem indeksów - wszystkie elementy wektora v poza tymi, których indeksy są podane w wektorze x;
do wskazywania podciągu elementów wektora v można też używać warunków logicznych.

f[3]

f[c(3,1,4,3)]

f[-5]

f[-seq(1,7,2)]

f[f<5]

W przypadku macierzy podajemy po przecinku indeksy interesujących nas wierszy i kolumn, np. polecenie A[2,3] zwróci element z drugiego wiersza i trzeciej kolumny. Jeśli przed lub po przecinku nic nie wpiszemy, to zostaną wybrane wszystkie elementy z danej kolumny lub wiersza.

A matrix: 2 × 3 of type dbl
a	1	2	-4
e	2	5	8

A[2, 3]

e: 8

A[, 2]

a: 2
e: 5

A[2, ]

Operatory logiczne

x==y - prawda, jeśli x jest równe y;
x!=y - prawda, jeśli x jest różne od y;
x&y - koniunkcja x i y (jeśli x i y są wektorami, to porównywane będą wszystkie odpowiadające sobie współrzędne);
x|y - alternatywa x i y (jeśli x i y są wektorami, to porównywane będą wszystkie odpowiadające sobie współrzędne);
!x - negacja x.

a = c(1, 0, 0, 1)
b = c(1, 1, 0, 0)

a&b

a|b

!a

Instrukcja warunkowa i pętle

Poniżej pokażemy na przykładach, jak możemy tworzyć pętle i instrukcje warunkowe.

Instrukcja if ... else:

if (warunek) {instrukcje_1} else {instrukcje2}

# Instrukcja warunkowa porównująca dwie liczby
a = 5
b = 3
if (a>b) {
    print('a jest większe od b')
    } else {
    print('b jest większe lub równe a')
    }

Pętla for:

for (iterator in kolekcja) {instrukcje}

# Pętla for wyliczająca kwadraty kolejnych liczb z wektora x
x = 1:10
for (i in x) {
    print(i^2)
    }

Pętla while:

while (warunek) {instrukcje}

# Pętla while wyliczająca kwadraty kolejnych liczb z wektora x
i = 0
while (i<10) {
    i = i+1
    print(i^2)
    }

Funkcje

Funkcje możemy zdefiniować w następujący sposób:

nazwa<-function(x1, x2, ..., xn) {instrukcje},

gdzie $x1,x2,\ldots, xn$ są argumentami funkcji.

Możemy podać dowolną liczbę argumentów, ale każdy z nich powinien mieć unikalną nazwę. Możemy też podać dla nich wartości domyślne, podając wartość po nazwie każdego argumentu:

function(x1=wartosc1, x2=wartosc2, ..., xn=wartoscn) {instrukcje}.

W przypadku, gdy funkcję da się zapisać za pomocą pojedynczej instrukcji, nawiasy klamrowe można pominąć, tzn. stosujemy schemat:

nazwa<-function(x1, x2, ..., xn) instrukcja.

Wynikiem działania funkcji będzie wartość wyznaczona w ostatniej linijce instrukcji lub argument instrukcji return().
Aby wywołać funkcję należy podać jej nazwę, a następnie w okrągłych nawiasach podać wartości jej argumentów. Jeśli chcemy podać wartości tylko dla wybranych argumentów (a dla pozostałych zastosować wartości domyślne), to powinniśmy podać nazwę argumentu, a następnie po znaku = podać jego wartość.

pole<-function(a=2, b=3) a*b
#definicja funkcji obliczającej pole prostokąta a wymiarach axb

pole() #zwraca pole prostokąta o domyślnych wymiarach tzn. 2x3

pole(3, 4) #zwraca pole prostokąta o wymiarach 3x4

pole(b=5) #zwraca pole prostokąta o wymiarach 2x5

Wykresy i diagramy

Program R oferuje bardzo szerokie możliwości wizualizacji danych. Podstawowa funkcja generująca wykresy to:

plot(x ,y, ...),

gdzie x i y to wektory zawierające odpowiednio pierwsze i drugie współrzędne punktów, które chcemy umieścić na wykresie. Jeśli podamy tylko wektor y, to domyślnie zostanie przyjęte, że wektor x to kolejne liczby naturalne od $1$ do $n$, gdzie $n$ to długość wektora y. W miejscu '...' możemy podawać najróżniejsze parametry związane z wyglądem wykresu. Wśród najważniejszych opcji, które możemy zdefiniować są:

type - kontroluje typ wykresu. Przykładowe opcje to:
- p - wykres punktowy (jest to opcja domyślna),
- l - wykres liniowy,
- b, o - wykresy liniowo-punktowe (różnica polega na sposobie łączenia punktów z liniami).
xlim, ylim - pozwalają ustalić graniczne wartości odpowiednio na osi $OX$ i $OY$ wykresu,
main - pozwala dodać główny tytuł do wykresu,
sub - pozwala dodać podpis / podtytuł do wykresu,
xlab, ylab - pozwalają dodać nazwy osi,
col - pozwala ustalić kolory punktów / linii umieszczanych na wykresie. Jako argumenty możemy podawać nazwy kolorów (np. blue) lub liczby naturalne,
pch - pozwala ustalić typ (kształt) punktów używanych na wykresie. Poniżej przedstawiono $25$ podstawowych typów punktów, wraz z odpowiadającymi im numerami,
cex - pozwala ustalić wielkość punktów,
lty - pozwala ustalić typ linii (dla wykresów liniowych). Typ można podać słownie lub za pomocą odpowiedniej liczby naturalnej. Podstawowe typy linii to (po nazwie podajemy też przypisaną jej liczbę naturalną):
- solid (1) - linia ciągła (jest to opcja domyślna),
- dashed (2) - linia kreskowana,
- dotted (3) - linia kropkowana.
lwd - pozwala ustalić szerokość linii.

#Zaczniemy od narysowania prostego wykresu punktowego
x = seq(-2, 1, 0.5)
y = c(1, 0, 1, 2, 3, -1, 2)
plot(x, y, pch=2:8, cex=2, col=1:7, main='Przykładowy wykres punktowy', sub='Różne rodzaje punktów')

# Jeśli zmienimy typ wykresu na liniowy, to podane punkty zostaną połączone łamaną
plot(x, y, type='l', lty='dashed', lwd=3, col='green', main='Przykładowy wykres liniowy', xlab='argumenty', ylab='wartosci')

Jeśli chcemy narysować wykres funkcji, dla której znamy wzór, możemy też zastosować następujące polecenie:

curve(f, from=NULL, to=NULL, n, add=FALSE, ...),

gdzie:

f - nazwa lub wzór funkcji,
from, to - minimalny i maksymalny argument, dla których będzie obliczana wartość funkcji,
n - liczba naturalna, która oznacza liczbę punktów, w których będzie obliczana wartość funkcji. Punkty te są rozmieszczone równomiernie w dziedzinie,
add - przyjmuje wartość TRUE, jeśli wykres ma być dorysowany do wcześniej istniejących wykresów i FALSE w przeciwnym przypadku.

Podobnie, jak w przypadku polecenia plot w miejscu ... można wpisać wiele różnych parametrów kontrolujących wygląd wykresu.

# Narysujemy wykres funkcji pierwiastek z x na przedziale [0, 10]
curve(sqrt, from=0, to=10, n=50, col='blue', lty=2, ylim=c(-1,3), main='Przykładowe wykresy funkcji matematycznych', ylab='y')

# Następnie dorysujemy wykres funkcji f(x) = 1/50*x^2-1
curve(1/50*x^2-1, from=0, to=10, col='red', lty=3, add=TRUE)
legend(0, 2.5, c('sqrt(x)', '1/50*x^2-1'), col=c('blue', 'red'), lty=c(2,3))

W R możemy też stworzyć wykresy słupkowe. Służy do tego następujące polecenie:

barplot(height, names.arg=NULL, horiz=FALSE, ...),

gdzie height oznacza wysokość kolejnych słupków, a names.arg etykiety kolejnych słupków. Jeśli horiz ma wartość TRUE, słupki rysowane są poziomo, w przeciwnym przypadku słupki rysowane są pionowe. Ponownie możemy też podać wiele innych argumentów wpływających na wygląd wykresu.

# Narysujmy wykres słupkowy przedstawiający liczebności grup ćwiczeniowych z Rachunku Prawdopodobieństwa
licz = c(18, 24, 21, 21)
grupy = c(1, 11, 12, 13)
barplot(licz, names.arg=grupy, col=10:13, main='Liczebność grup ćwiczeniowych z Rachunku Prawdopodobieństwa')

Literatura

Marek Gągolewski, _Programowanie w języku R. Analiza danych, obliczenia, symulacje. Wydawnictwo Naukowe PWN 2014.
Przemysław Biecek, _Przewodnik po pakiecie R, GiS, 2017 (pierwsze rodziały tej książki są dostępne na stronie autora).
Wiele użytecznych materiałów można też znaleźć na następującej stronie. W szczególności, można znaleźć tam krótkie wprowadzenie do R w języku polskim.

185 KiB Raw Permalink Blame History Unescape Escape