8.7 KiB
- Wygładzanie w n-gramowych modelach języka
Wygładzanie w n-gramowych modelach języka
Dlaczego wygładzanie?
Wyobraźmy sobie urnę, w której znajdują się kule w $m$ kolorach (ściślej: w co najwyżej $m$ kolorach, może w ogóle nie być kul w danym kolorze). Nie wiemy, ile jest ogółem kul w urnie i w jakiej liczbie występuje każdy z kolorów.
Losujemy ze zwracaniem (to istotne!) $T$ kul, załóżmy, że wylosowaliśmy w poszczególnych kolorach $\{k_1,\dots,k_m\}$ kul (tzn. pierwszą kolor wylosowaliśmy $k_1$ razy, drugi kolor — $k_2$ razy itd.). Rzecz jasna, $\sum_{i=1}^m k_i = T$.
Jak powinniśmy racjonalnie szacować prawdopodobieństwa wylosowania kuli w $i$-tym kolorze ($p_i$)?
Wydawałoby się wystarczyłoby liczbę wylosowanych kul w danym kolorze podzielić przez liczbę wszystkich prób:
$$p_i = \frac{k_i}{T}.$$
Wygładzanie — przykład
Rozpatrzmy przykład z 3 kolorami (wiemy, że w urnie mogą być urny żółte, zielone i czerwone, tj. $m=3$) i 4 losowaniami ($T=4$):
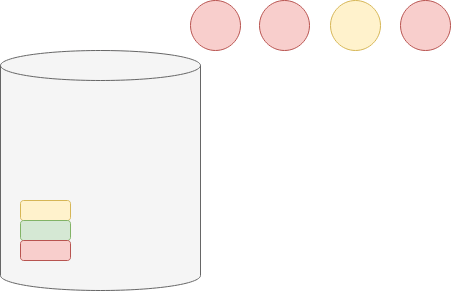
Gdybyśmy w prosty sposób oszacowali prawdopodobieństwa, doszlibyśmy do wniosku, że prawdopodobieństwo wylosowania kuli czerwonej wynosi 3/4, żółtej — 1/4, a zielonej — 0. Wartości te są jednak dość problematyczne:
- Za bardzo przywiązujemy się do naszej skromnej próby, potrzebowalibyśmy większej liczby losowań, żeby być bardziej pewnym naszych estymacji.
- W szczególności stwierdzenie, że prawdopodobieństwo wylosowania kuli zielonej wynosi 0 jest bardzo mocnym stwierdzeniem (twierdzimy, że NIEMOŻLIWE jest wylosowanie kuli zielonej), dopiero większa liczba prób bez wylosowania zielonej kuli mogłaby sugerować prawdopodobieństwo bliskie zeru.
- Zauważmy, że niemożliwe jest wylosowanie ułamka kuli, jeśli w rzeczywistości 10% kul jest żółtych to nie oznacza się wylosujemy $4\frac{1}{10} = \frac{2}{5}$ kuli. Prawdopodobnie wylosujemy jedną kulę żółtą albo żadną. Wylosowanie dwóch kul żółtych byłoby możliwe, ale mniej prawdopodobne. Jeszcze mniej prawdopodobne byłoby wylosowanie 3 lub 4 kul żółtych.
Idea wygładzania
Wygładzanie (ang. smoothing) polega na tym, że „uszczknąć” nieco masy prawdopodobieństwa zdarzeniom wskazywanym przez eksperyment czy zbiór uczący i rozdzielić ją między mniej prawdopodobne zdarzenia.
Wygładzanie +1
Najprostszy sposób wygładzania to wygładzania +1, nazywane też wygładzaniem Laplace'a, zdefiniowane za pomocą następującego wzoru:
$$p_i = \frac{k_i+1}{T+m}.$$
W naszym przypadku z urną prawdopodobieństwo wylosowania kuli czerwonej określimy na $\frac{3+1}{4+3} = \frac{4/7}$, kuli żółtej — $\frac{1+1}{4+3}=2/7$, zielonej — $\frac{0+1}{4+3}=1/7$. Tym samym, kula zielona uzyskała niezerowe prawdopodobieństwo, żółta — nieco zyska, zaś czerwona — straciła.
Własności wygładzania +1
Zauważmy, że większa liczba prób $m$, tym bardziej ufamy naszemu eksperymentowi (czy zbiorowi uczącemu) i tym bardziej zbliżamy się do niewygładzonej wartości:
$$\lim_{m \rightarrow \infty} \frac{k_i +1}{T + m} = \frac{k_i}{T}.$$
Inna dobra, zdroworozsądkowo, własność to to, że prawdopodobieństwo nigdy nie będzie zerowe:
$$frac{k_i + 1}{T + m} > 0.$$
Wygładzanie w unigramowym modelu języku
Analogia do urny
Unigramowy model języka, abstrakcyjnie, dokładnie realizuje scenariusz losowania kul z urny: $m$ to liczba wszystkich wyrazów (czyli rozmiar słownika $|V|$), $k_i$ to ile razy w zbiorze uczącym pojawił się $i$-ty wyraz słownika, $T$ — długość zbioru uczącego.
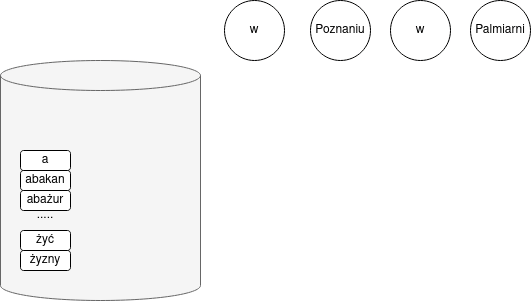
A zatem przy użyciu wygładzania +1 w następujący sposób estymować będziemy prawdopodobieństwo słowa $w$:
$$P(w) = \fraq{\# w + 1}{|C| + |V|}.$$
Wygładzanie $+\alpha$
W modelowaniu języka wygładzanie $+1$ daje zazwyczaj niepoprawne wyniki, dlatego częściej zamiast wartości 1 używa się współczynnika $0 < \alpha < 1$. W innych praktycznych zastosowaniach statystyki przyjmuje się $\alpha = \frac{1}{2}$, ale w przypadku n-gramowych modeli języka i to będzie zbyt duża wartość.
W jaki sposób ustalić wartość $\alpha$? Można $\alpha$ potraktować $\alpha$ jako hiperparametr i dostroić ją na odłożonym zbiorze.
Jak wybrać wygładzanie?
Jak ocenić, który sposób wygładzania jest lepszy? Jak wybrać $\alpha$ w czasie dostrajania?
Najprościej można sprawdzić estymowane prawdopodobieństwa na zbiorze strojącym (developerskim). Dla celów poglądowych bardziej czytelny będzie podział zbioru uczącego na dwie równe części — będziemy porównywać częstości estymowane na jednej połówce korpusu z rzeczywistymi, empirycznymi częstościami z drugiej połówki.
Wyniki będziemy przedstawiać w postaci tabeli, gdzie w poszczególnych wierszach będziemy opisywać częstości estymowane dla wszystkich wyrazów, które pojawiły się określoną liczbę razy w pierwszej połówce korpusu.
Ostatecznie możemy też po prostu policzyć perplexity na zbiorze testowym
Wygładzanie Gooda-Turinga
Inna metoda — wygładzanie Gooda-Turinga — polega na zliczaniu, ile $n$-gramów (na razie rozpatrujemy model unigramowy, więc po prostu pojedynczych wyrazów) wystąpiło zadaną liczbę razy. Niech $N_r$ oznacza właśnie, ile $n$-gramów wystąpiło dokładnie $r$ razy; na przykład $N_1$ oznacza liczbę hapax legomena.
W metodzie Gooda-Turinga używamy następującej estymacji:
$$p(w) = \frac{\# w + 1}{|C|}\frac{N_{r+1}}{N_r}.$$
Wygładzanie dla $n$-gramów
Rzadkość danych
W wypadku bigramów, trigramów itd. jeszcze dotkliwy staje się problem rzadkości danych (data sparsity). Przestrzeń możliwych zdarzeń jest jeszcze większa ($|V|^2$ dla bigramów), więc estymacje stają się jeszcze mniej pewne.
Back-off
Dla $n$-gramów, gdzie $n>1$, nie jesteśmy ograniczeni do wygładzania $+1$, $+k$ czy Gooda-Turinga. W przypadku rzadkich $n$-gramów, w szczególności gdy $n$-gram w ogóle się nie pojawił w korpusie, możemy „zejść” na poziom krótszych $n$-gramów. Na tym polega back-off.
Otóż jeśli $\# w_{i-n+1}\ldots w_{i-1} > 0$, wówczas estymujemy prawdopodobieństwa w tradycyjny sposób:
$$P_B(w_i|w_{i-n+1}\ldots w_{i-1}) = d_n(w_{i-n+1}\ldots w_{i-1}\ldots w_{i-1}) P(w_i|w_{i-n+1}\ldots w_{i-1})$$
W przeciwnym razie, rozpatrujemy rekurencyjnie krótszy $n$-gram:
$$P_B(w_i|w_{i-n+1}\ldots w_{i-1}) = \delta_n(w_{i-n+1}\ldots w_{i-1}\ldots w_{i-1}) P_B(w_i|w_{i-n+2}\ldots w_{i-1}).$$
Technicznie, aby $P_B$ stanowiło rozkład prawdopodobieństwa, trzeba dobrać współczynniki $d$ i $\delta$.
Interpolacja
Alternatywą do metody back-off jest interpolacja — zawsze z pewnym współczynnikiem uwzględniamy prawdopodobieństwa dla krótszych $n$-gramów:
$$P_I(w_i|w_{i-n+1}\ldots w_{i-1}) = \lambda P(w_i|w_{i-n+1}\dots w_{i-1}) + (1-\lambda) P_I(w_i|w_{i-n+2}\dots w_{i-1}).$$
Na przykład, dla trigramów:
$$P_I(w_i|w_{i-2}w_{i-1}) = \lambda P_(w_i|w_{i-2}w_{i-1}) + (1-\lambda)(\lambda P(w_i|w_{i-1}) + (1-\lambda)P_I(w_i)).$$
Uwzględnianie różnorodności
Różnorodność kontynuacji
Zauważmy, że słowa mogą bardzo różnić się co do różnorodności kontynuacji. Na przykład po słowie szop spodziewamy się raczej tylko słowa pracz, każde inne, niewidziane w zbiorze uczącym, będzie zaskakujące. Dla porównania słowo seledynowy ma bardzo dużo możliwych kontynuacji i powinniśmy przeznaczyć znaczniejszą część masy prawdopodobieństwa na kontynuacje niewidziane w zbiorze uczącym.
Różnorodność kontynuacji bierze pod uwagę metoda wygładzania Wittena-Bella, będącą wersją interpolacji.
Wprowadźmy oznaczenie na liczbę możliwych kontynuacji $n-1$-gramu $w_1\ldots w_{n-1}$:
$$N_{1+}(w_1\ldots w_{n-1}\dot\bullet) = |\{w_n : \# w_1\ldots w_{n-1}w_n > 0\}|.$$
Teraz zastosujemy interpolację z następującą wartością parametru $1-\lambda$, sterującego wagą, jaką przypisujemy do krótszych $n$-gramów:
$$1 - \lambda = \frag{N_{1+}(w_1\ldots w_{n-1}\dot\bullet)}{N_{1+}(w_1\ldots w_{n-1}\dot\bullet) + \# w_1\ldots w_{n-1}}.$$
Wygładzanie Knesera-Neya
Zamiast brać pod uwagę różnorodność kontynuacji, możemy rozpatrywać różnorodność historii — w momencie liczenia prawdopodobieństwa dla unigramów dla interpolacji (nie ma to zastosowania dla modeli unigramowych). Na przykład dla wyrazu Jork spodziewamy się tylko bigramu Nowy Jork, a zatem przy interpolacji czy back-off prawdopodobieństwo unigramowe powinno być niskie.
Wprowadźmy oznaczenia na liczbę możliwych historii:
$$N_{1+}(\bullet w) = |\{w_j : \# w_jw > 0\}|$$.
W metodzie Knesera-Neya w następujący sposób estymujemy prawdopodobieństwo unigramu:
$$P(w) = \frac{N_{1+}(\bullet w)}{\sum_{w_j} N_{1+}(\bullet w_j)}.$$