20 KiB

Modelowanie języka
09. Zanurzenia słów (Word2vec) [wykład]
Filip Graliński (2022)

Zanurzenia słów (Word2vec)
W praktyce stosowalność słowosieci okazała się zaskakująco ograniczona. Większy przełom w przetwarzaniu języka naturalnego przyniosły wielowymiarowe reprezentacje słów, inaczej: zanurzenia słów.
„Wymiary” słów
Moglibyśmy zanurzyć (ang. _embed) w wielowymiarowej przestrzeni, tzn. zdefiniować odwzorowanie $E \colon V \rightarrow \mathcal{R}^m$ dla pewnego $m$ i określić taki sposób estymowania prawdopodobieństw $P(u|v)$, by dla par $E(v)$ i $E(v')$ oraz $E(u)$ i $E(u')$ znajdujących się w pobliżu (według jakiejś metryki odległości, na przykład zwykłej odległości euklidesowej):
$$P(u|v) \approx P(u'|v').$$
$E(u)$ nazywamy zanurzeniem (embeddingiem) słowa.
Wymiary określone z góry?
Można by sobie wyobrazić, że $m$ wymiarów mogłoby być z góry określonych przez lingwistę. Wymiary te byłyby związane z typowymi „osiami” rozpatrywanymi w językoznawstwie, na przykład:
- czy słowo jest wulgarne, pospolite, potoczne, neutralne czy książkowe?
- czy słowo jest archaiczne, wychodzące z użycia czy jest neologizmem?
- czy słowo dotyczy kobiet, czy mężczyzn (w sensie rodzaju gramatycznego i/lub socjolingwistycznym)?
- czy słowo jest w liczbie pojedynczej czy mnogiej?
- czy słowo jest rzeczownikiem czy czasownikiem?
- czy słowo jest rdzennym słowem czy zapożyczeniem?
- czy słowo jest nazwą czy słowem pospolitym?
- czy słowo opisuje konkretną rzecz czy pojęcie abstrakcyjne?
- …
W praktyce okazało się jednak, że lepiej, żeby komputer uczył się sam możliwych wymiarów — z góry określamy tylko $m$ (liczbę wymiarów).
Bigramowy model języka oparty na zanurzeniach
Zbudujemy teraz najprostszy model język oparty na zanurzeniach. Będzie to właściwie najprostszy neuronowy model języka, jako że zbudowany model można traktować jako prostą sieć neuronową.
Słownik
W typowym neuronowym modelu języka rozmiar słownika musi być z góry
ograniczony. Zazwyczaj jest to liczba rzędu kilkudziesięciu wyrazów —
po prostu będziemy rozpatrywać $|V|$ najczęstszych wyrazów, pozostałe zamienimy
na specjalny token <unk> reprezentujący nieznany (_unknown) wyraz.
Aby utworzyć taki słownik, użyjemy gotowej klasy Vocab z pakietu torchtext:
from itertools import islice
import regex as re
import sys
from torchtext.vocab import build_vocab_from_iterator
def get_words_from_line(line):
line = line.rstrip()
yield '<s>'
for m in re.finditer(r'[\p{L}0-9\*]+|\p{P}+', line):
yield m.group(0).lower()
yield '</s>'
def get_word_lines_from_file(file_name):
with open(file_name, 'r') as fh:
for line in fh:
yield get_words_from_line(line)
vocab_size = 20000
vocab = build_vocab_from_iterator(
get_word_lines_from_file('/home/filipg/in.txt'),
max_tokens = vocab_size,
specials = ['<unk>'])
vocab['jest']10518
vocab.lookup_tokens([0, 1, 2, 10, 12345])['<unk>', 'the', ',', 'that', 'dividual']
Definicja sieci
Naszą prostą sieć neuronową zaimplementujemy używając frameworku PyTorch.
from torch import nn
import torch
embed_size = 100
class SimpleBigramNeuralLanguageModel(nn.Module):
def __init__(self, vocabulary_size, embedding_size):
super(SimpleBigramNeuralLanguageModel, self).__init__()
self.model = nn.Sequential(
nn.Embedding(vocabulary_size, embedding_size),
nn.Linear(embedding_size, vocabulary_size),
nn.Softmax()
)
def forward(self, x):
return self.model(x)
model = SimpleBigramNeuralLanguageModel(vocab_size, embed_size)
vocab.set_default_index(vocab['<unk>'])
ixs = torch.tensor(vocab.forward(['dog']))
out = model(ixs)
out[0][vocab['jest']]/home/filipg/.local/lib/python3.10/site-packages/torch/nn/modules/container.py:217: UserWarning: Implicit dimension choice for softmax has been deprecated. Change the call to include dim=X as an argument. input = module(input)
tensor(2.9242e-05, grad_fn=<SelectBackward0>)
Teraz wyuczmy model. Wpierw tylko potasujmy nasz plik:
shuf < opensubtitlesA.pl.txt > opensubtitlesA.pl.shuf.txt
from torch.utils.data import IterableDataset
import itertools
def look_ahead_iterator(gen):
prev = None
for item in gen:
if prev is not None:
yield (prev, item)
prev = item
class Bigrams(IterableDataset):
def __init__(self, text_file, vocabulary_size):
self.vocab = build_vocab_from_iterator(
get_word_lines_from_file(text_file),
max_tokens = vocabulary_size,
specials = ['<unk>'])
self.vocab.set_default_index(self.vocab['<unk>'])
self.vocabulary_size = vocabulary_size
self.text_file = text_file
def __iter__(self):
return look_ahead_iterator(
(self.vocab[t] for t in itertools.chain.from_iterable(get_word_lines_from_file(self.text_file))))
train_dataset = Bigrams('/home/filipg/in.txt', vocab_size)from torch.utils.data import DataLoader
next(iter(train_dataset))(19, 236)
from torch.utils.data import DataLoader
next(iter(DataLoader(train_dataset, batch_size=5)))[tensor([ 2, 5, 51, 3481, 231]), tensor([ 5, 51, 3481, 231, 4])]
device = 'cuda'
model = SimpleBigramNeuralLanguageModel(vocab_size, embed_size).to(device)
data = DataLoader(train_dataset, batch_size=5000)
optimizer = torch.optim.Adam(model.parameters())
criterion = torch.nn.NLLLoss()
model.train()
step = 0
for x, y in data:
x = x.to(device)
y = y.to(device)
optimizer.zero_grad()
ypredicted = model(x)
loss = criterion(torch.log(ypredicted), y)
if step % 100 == 0:
print(step, loss)
step += 1
loss.backward()
optimizer.step()
torch.save(model.state_dict(), 'model1.bin')0 tensor(10.1095, device='cuda:0', grad_fn=<NllLossBackward0>) 100 tensor(8.4894, device='cuda:0', grad_fn=<NllLossBackward0>) 200 tensor(7.6437, device='cuda:0', grad_fn=<NllLossBackward0>) 300 tensor(7.0887, device='cuda:0', grad_fn=<NllLossBackward0>) 400 tensor(6.7963, device='cuda:0', grad_fn=<NllLossBackward0>) 500 tensor(6.3892, device='cuda:0', grad_fn=<NllLossBackward0>) 600 tensor(6.1413, device='cuda:0', grad_fn=<NllLossBackward0>) 700 tensor(6.1875, device='cuda:0', grad_fn=<NllLossBackward0>) 800 tensor(6.1369, device='cuda:0', grad_fn=<NllLossBackward0>) 900 tensor(5.9865, device='cuda:0', grad_fn=<NllLossBackward0>) 1000 tensor(5.9185, device='cuda:0', grad_fn=<NllLossBackward0>) 1100 tensor(5.9149, device='cuda:0', grad_fn=<NllLossBackward0>) 1200 tensor(5.8374, device='cuda:0', grad_fn=<NllLossBackward0>) 1300 tensor(5.7507, device='cuda:0', grad_fn=<NllLossBackward0>) 1400 tensor(5.7998, device='cuda:0', grad_fn=<NllLossBackward0>) 1500 tensor(5.7555, device='cuda:0', grad_fn=<NllLossBackward0>) 1600 tensor(5.7237, device='cuda:0', grad_fn=<NllLossBackward0>) 1700 tensor(5.6886, device='cuda:0', grad_fn=<NllLossBackward0>) 1800 tensor(5.7297, device='cuda:0', grad_fn=<NllLossBackward0>) 1900 tensor(5.7816, device='cuda:0', grad_fn=<NllLossBackward0>) 2000 tensor(5.7083, device='cuda:0', grad_fn=<NllLossBackward0>) 2100 tensor(5.7132, device='cuda:0', grad_fn=<NllLossBackward0>) 2200 tensor(5.8103, device='cuda:0', grad_fn=<NllLossBackward0>) 2300 tensor(5.7318, device='cuda:0', grad_fn=<NllLossBackward0>) 2400 tensor(5.6933, device='cuda:0', grad_fn=<NllLossBackward0>) 2500 tensor(5.5518, device='cuda:0', grad_fn=<NllLossBackward0>) 2600 tensor(5.5967, device='cuda:0', grad_fn=<NllLossBackward0>) 2700 tensor(5.7234, device='cuda:0', grad_fn=<NllLossBackward0>) 2800 tensor(5.5497, device='cuda:0', grad_fn=<NllLossBackward0>) 2900 tensor(5.6449, device='cuda:0', grad_fn=<NllLossBackward0>) 3000 tensor(5.6020, device='cuda:0', grad_fn=<NllLossBackward0>) 3100 tensor(5.6002, device='cuda:0', grad_fn=<NllLossBackward0>) 3200 tensor(5.5400, device='cuda:0', grad_fn=<NllLossBackward0>) 3300 tensor(5.5242, device='cuda:0', grad_fn=<NllLossBackward0>) 3400 tensor(5.6654, device='cuda:0', grad_fn=<NllLossBackward0>) 3500 tensor(5.7363, device='cuda:0', grad_fn=<NllLossBackward0>) 3600 tensor(5.4690, device='cuda:0', grad_fn=<NllLossBackward0>) 3700 tensor(5.6095, device='cuda:0', grad_fn=<NllLossBackward0>) 3800 tensor(5.6472, device='cuda:0', grad_fn=<NllLossBackward0>)
Policzmy najbardziej prawdopodobne kontynuacje dla zadanego słowa:
device = 'cuda'
model = SimpleBigramNeuralLanguageModel(vocab_size, embed_size).to(device)
model.load_state_dict(torch.load('model1.bin'))
model.eval()
ixs = torch.tensor(vocab.forward(['dla'])).to(device)
out = model(ixs)
top = torch.topk(out[0], 10)
top_indices = top.indices.tolist()
top_probs = top.values.tolist()
top_words = vocab.lookup_tokens(top_indices)
list(zip(top_words, top_indices, top_probs))[('ciebie', 73, 0.1580502986907959), ('mnie', 26, 0.15395283699035645), ('<unk>', 0, 0.12862136960029602), ('nas', 83, 0.0410110242664814), ('niego', 172, 0.03281523287296295), ('niej', 245, 0.02104802615940571), ('siebie', 181, 0.020788608118891716), ('którego', 365, 0.019379809498786926), ('was', 162, 0.013852755539119244), ('wszystkich', 235, 0.01381855271756649)]Teraz zbadajmy najbardziej podobne zanurzenia dla zadanego słowa:
vocab = train_dataset.vocab
ixs = torch.tensor(vocab.forward(['kłopot'])).to(device)
out = model(ixs)
top = torch.topk(out[0], 10)
top_indices = top.indices.tolist()
top_probs = top.values.tolist()
top_words = vocab.lookup_tokens(top_indices)
list(zip(top_words, top_indices, top_probs))[('.', 3, 0.404473215341568), (',', 4, 0.14222915470600128), ('z', 14, 0.10945753753185272), ('?', 6, 0.09583134204149246), ('w', 10, 0.050338443368673325), ('na', 12, 0.020703863352537155), ('i', 11, 0.016762692481279373), ('<unk>', 0, 0.014571071602404118), ('...', 15, 0.01453721895813942), ('</s>', 1, 0.011769450269639492)]cos = nn.CosineSimilarity(dim=1, eps=1e-6)
embeddings = model.model[0].weight
vec = embeddings[vocab['poszedł']]
similarities = cos(vec, embeddings)
top = torch.topk(similarities, 10)
top_indices = top.indices.tolist()
top_probs = top.values.tolist()
top_words = vocab.lookup_tokens(top_indices)
list(zip(top_words, top_indices, top_probs))[('poszedł', 1087, 1.0), ('idziesz', 1050, 0.4907470941543579), ('przyjeżdża', 4920, 0.45242372155189514), ('pojechałam', 12784, 0.4342481195926666), ('wrócił', 1023, 0.431664377450943), ('dobrać', 10351, 0.4312002956867218), ('stałeś', 5738, 0.4258835017681122), ('poszła', 1563, 0.41979148983955383), ('trafiłam', 18857, 0.4109022617340088), ('jedzie', 1674, 0.4091658890247345)]Zapis przy użyciu wzoru matematycznego
Powyżej zaprogramowaną sieć neuronową można opisać następującym wzorem:
$$\vec{y} = \operatorname{softmax}(CE(w_{i-1}),$$
gdzie:
- $w_{i-1}$ to pierwszy wyraz w bigramie (poprzedzający wyraz),
- $E(w)$ to zanurzenie (embedding) wyrazy $w$ — wektor o rozmiarze $m$,
- $C$ to macierz o rozmiarze $|V| \times m$, która rzutuje wektor zanurzenia w wektor o rozmiarze słownika,
- $\vec{y}$ to wyjściowy wektor prawdopodobieństw o rozmiarze $|V|$.
Hiperparametry
Zauważmy, że nasz model ma dwa hiperparametry:
- $m$ — rozmiar zanurzenia,
- $|V|$ — rozmiar słownika, jeśli zakładamy, że możemy sterować
rozmiarem słownika (np. przez obcinanie słownika do zadanej liczby
najczęstszych wyrazów i zamiany pozostałych na specjalny token, powiedzmy,
<UNK>.
Oczywiście możemy próbować manipulować wartościami $m$ i $|V|$ w celu polepszenia wyników naszego modelu.
Pytanie: dlaczego nie ma sensu wartość $m \approx |V|$ ? dlaczego nie ma sensu wartość $m = 1$?
Diagram sieci
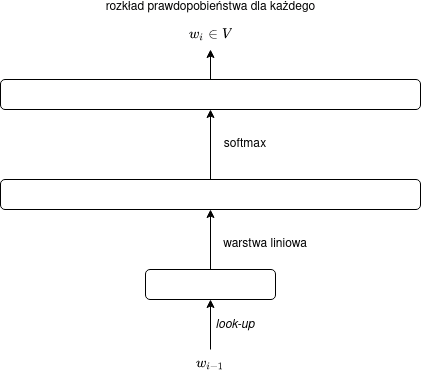
Jako że mnożenie przez macierz ($C$) oznacza po prostu zastosowanie warstwy liniowej, naszą sieć możemy interpretować jako jednowarstwową sieć neuronową, co można zilustrować za pomocą następującego diagramu:
Zanurzenie jako mnożenie przez macierz
Uzyskanie zanurzenia ($E(w)$) zazwyczaj realizowane jest na zasadzie odpytania (look-up_). Co ciekawe, zanurzenie można intepretować jako mnożenie przez macierz zanurzeń (embeddingów) $E$ o rozmiarze $m \times |V|$ — jeśli słowo będziemy na wejściu kodowali przy użyciu wektora z gorącą jedynką (one-hot encoding_), tzn. słowo $w$ zostanie podane na wejściu jako wektor $\vec{1_V}(w) = [0,\ldots,0,1,0\ldots,0]$ o rozmiarze $|V|$ złożony z samych zer z wyjątkiem jedynki na pozycji odpowiadającej indeksowi wyrazu $w$ w słowniku $V$.
Wówczas wzór przyjmie postać:
$$\vec{y} = \operatorname{softmax}(CE\vec{1_V}(w_{i-1})),$$
gdzie $E$ będzie tym razem macierzą $m \times |V|$.
Pytanie: czy $\vec{1_V}(w)$ intepretujemy jako wektor wierszowy czy kolumnowy?
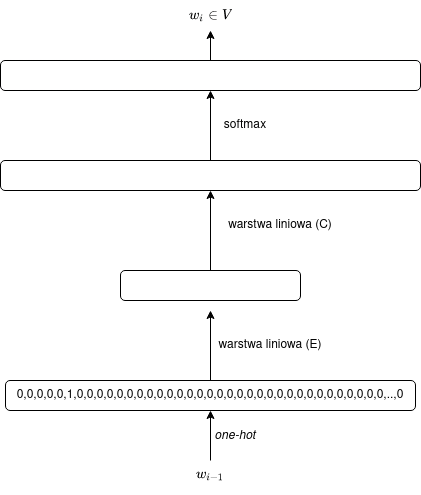
W postaci diagramu można tę interpretację zilustrować w następujący sposób: