15 KiB

Modelowanie języka
11. Model worka słów w sieci feed-forward [wykład]
Filip Graliński (2022)

Model worka słów w sieci feed-forward
Jak stwierdziliśmy w poprzednim wykładzie, dwuwarstwowy n-gramowy model języka może działać dla stosunkowo dużego $n$. Zauważmy jednak, że istnieje pewna słabość tego modelu. Otóż o ile intuicyjnie ma sens odróżniać słowo poprzedzające, słowo występujące dwie pozycje wstecz i zapewne trzy pozycje wstecz, a zatem uczyć się osobnych macierzy $C_{-1}$, $C_{-2}$, $C_{-3}$ to różnica między wpływem słowa występującego cztery pozycje wstecz i pięć pozycji wstecz jest już raczej nieistotna; innymi słowy różnica między macierzami $C_{-4}$ i $C_{-5}$ będzie raczej niewielka i sieć niepotrzebnie będzie uczyła się dwukrotnie podobnych wag. Im dalej wstecz, tym różnica wpływu będzie jeszcze mniej istotna, można np. przypuszczać, że różnica między $C_{-10}$ i $C_{-13}$ nie powinna być duża.
Spróbujmy najpierw zaproponować radykalne podejście, w którym nie będziemy w ogóle uwzględniać pozycji słów (lub będziemy je uwzględniać w niewielkim stopniu), później połączymy to z omówionym wcześniej modelem $n$-gramowym.
Agregacja wektorów
Zamiast patrzeć na kilka poprzedzających słów, można przewidywać na podstawie całego ciągu słów poprzedzających odgadywane słowo. Zauważmy jednak, że sieć neuronowa musi mieć ustaloną strukturę, nie możemy zmieniać jej rozmiaru. Musimy zatem najpierw zagregować cały ciąg do wektora o stałej długości. Potrzebujemy zatem pewnej funkcji agregującej $A$, takiej by $A(w_1,\dots,w_{i-1})$ było wektorem o stałej długości, niezależnie od $i$.
Worek słów
Najprostszą funkcją agregującą jest po prostu… suma. Dodajemy po prostu zanurzenia słów:
$$A(w_1,\dots,w_{i-1}) = E(w_1) + \dots + E(w_{i-1}) = \sum_{j=1}^{i-1} E(w_j).$$
Uwaga: zanurzenia słów nie zależą od pozycji słowa (podobnie było w wypadku n-gramowego modelu!).
Jeśli rozmiar zanurzenia (embeddingu) wynosi $m$, wówczas rozmiar wektora uzyskanego dla całego poprzedzającego tekstu wynosi również $m$.
Proste dodawanie wydaje się bardzo „prostacką” metodą, a jednak suma wektorów słów jest zaskakująco skuteczną metodą zanurzenia (embedowania) całych tekstów (doc2vec). Prostym wariantem dodawania jest obliczanie średniej wektorów:
$$A(w_1,\dots,w_{i-1}) = \frac{E(w_1) + \dots + E(w_{i-1})}{i-1} = \frac{\sum_{j=1}^{i-1} E(w_j)}{i-1}.$$
Tak czy siak uzyskany wektor nie zależy od kolejności słów (dodawanie jest przemienne i łączne!). Mówimy więc o worku słów (_bag of words, BoW) — co ma symbolizować fakt, że słowa są przemieszane, niczym produkty w torbie na zakupy.
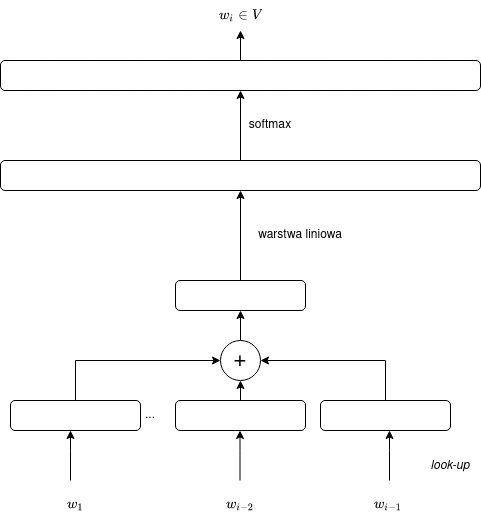
Schemat graficzny modelu typu worek słów
Po zanurzeniu całego poprzedzającego tekstu postępujemy podobnie jak w modelu bigramowym — rzutujemy embedding na długi wektor wartości, na którym stosujemy funkcję softmax:
Odpowiada to wzorowi:
$$y = \operatorname{softmax}(C\sum_{j=1}^{i-1} E(w_j)).$$
Jak traktować powtarzające się słowa?
Według wzoru podanego wyżej, jeśli słowo w poprzedzającym tekście pojawia się więcej niż raz, jego embedding zostanie zsumowany odpowiednią liczbę razy. Na przykład embedding tekstu _to be or not to be będzie wynosił:
$$E(\mathrm{to}) + E(\mathrm{be}) + E(\mathrm{or}) + E(\mathrm{not}) + E(\mathrm{to}) + E(\mathrm{be}) = 2E(\mathrm{to}) + 2E(\mathrm{be}) + E(\mathrm{or}) + E(\mathrm{not}).$$
Innymi słowy, choć w worku słów nie uwzględniamy kolejności słów, to liczba wystąpień ma dla nas ciągle znaczenie. Można powiedzieć, że traktujemy poprzedzający tekst jako multizbiór (struktura matematyczna, w której nie uwzględnia się kolejności, choć zachowana jest informacja o liczbie wystąpień).
Zbiór słów
Oczywiście moglibyśmy przy agregowaniu zanurzeń pomijać powtarzające się słowa, a zatem zamiast multizbioru słów rozpatrywać po prostu ich zbiór:
$$A(w_1,\dots,w_{i-1}) = \sum_{w \in \{w_1,\dots,w_{i-1}\}} E(w).$$
Jest kwestią dyskusyjną, czy to lepsze czy gorsze podejście — w końcu liczba wystąpień np. słów _Ukraina czy Polska może wpływać w jakimś stopniu na prawdopodobieństwo kolejnego słowa (_Kijów czy _Warszawa?).
Worek słów a wektoryzacja tf
Wzór na sumę zanurzeń słów można przekształcić w taki sposób, by sumować po wszystkich słowach ze słownika, zamiast po słowach rzeczywiście występujących w tekście:
$$A(w_1,\dots,w_{i-1}) = \sum_{j=1}^{i-1} E(w_j) = \sum_{w \in V} #wE(w)$$
gdzie $#w$ to liczba wystąpień słowa $w$ w ciagu $w_1,\dots,w_{i-1}$ (w wielu przypadkach równa zero!).
Jeśli teraz zanurzenia będziemy reprezentować jako macierz $E$ (por. poprzedni wykład), wówczas sumę można przedstawić jako iloczyn macierzy $E$ i pewnego wektora:
$$A(w_1,\dots,w_{i-1}) = E(w) [#w^1,\dots,#w^{|V|}]^T.$$
(Odróżniamy $w^i$ jako $i$-ty wyraz w słowniku $V$ od $w_i$ jako $i$-tego wyraz w rozpatrywanym ciągu).
Zwróćmy uwagę, że wektor $[#w_1,\dots,#w_{|V|}]$ to po prostu reprezentacja wektora poprzedzającego tekstu (tj. ciągu $(w_1,\dots,w_{i-1})$) przy użyciu schematu wektoryzacji tf (_term frequencyrzadkie, tj. na wielu pozycjach zawierają zera.
Innymi słowy, nasz model języka _bag of words można przedstawić za pomocą wzoru:
$$y = \operatorname{softmax}(C\operatorname{tf}(w_1,\dots,w_{i-1})),$$
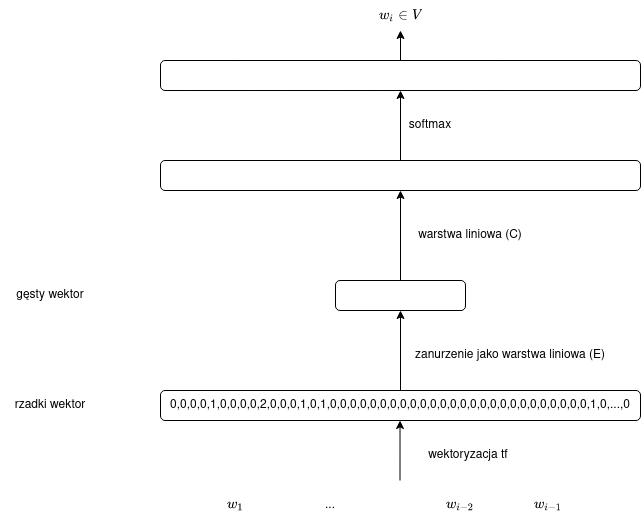
co można zilustrować w następujący sposób:
Można stwierdzić, że zanurzenie tekstu przekształca rzadki, długi wektor tf w gęsty, krótki wektor.
Ważenie słów
Czy wszystkie słowa są tak samo istotne? Rzecz jasna, nie:
- jak już wiemy z naszych rozważań dotyczących n-gramowych modeli języka, słowa bezpośrednio poprzedzające odgadywany wyraz mają większy wpływ niż słowa wcześniejsze; intuicyjnie, wpływ słów stopniowo spada — tym bardziej, im bardziej słowo jest oddalone od słowa odgadywanego;
- jak wiemy z wyszukiwania informacji, słowa, które występują w wielu tekstach czy dokumentach, powinny mieć mniejsze znaczenie, w skrajnym przypadku słowa występujące w prawie każdym tekście (_że, w, i itd.) powinny być praktycznie pomijane jako _stop words (jeśli rozpatrywać je w „masie” worka słów — oczywiście to, czy słowo poprzedzające odgadywane słowo to _że, w czy i ma olbrzymie znaczenie!).
Zamiast po prostu dodawać zanurzenia, można operować na sumie (bądź średniej) ważonej:
$$\sum_{j=1}^{i-1} \omega(j, w_j)E(w_j),$$
gdzie $\omega(j, w_j)$ jest pewną wagą, która może zależeć od pozycji $j$ lub samego słowa $w_j$.
Uwzględnienie pozycji
Można w pewnym stopniu złamać „workowatość” naszej sieci przez proste uwzględnienie pozycji słowa, np. w taki sposób:
$$\omega(j, w_j) = \beta^{i-j-1},$$
dla pewnego hiperparametru $\beta$. Na przykład jeśli $\beta=0,9$, wówczas słowo bezpośrednio poprzedzające dane słowo ma $1 / 0,9^9 \approx 2,58$ większy wpływ niż słowo występujące 10 pozycji wstecz.
Odwrócona częstość dokumentowa
Aby większą wagę przykładać do słów występujących w mniejszej liczbie dokumentów, możemy użyć, znanej z wyszukiwania informacji, odwrotnej częstości dokumentowej (_inverted document frequency, idf):
$$\omega(j, w_j) = \operatorname{idf}_S(w_j) = \operatorname{log}\frac{|S|}{\operatorname{df}_S(w_j)},$$
gdzie:
- $S$ jest pewną kolekcją dokumentów czy tekstów, z którego pochodzi przedmiotowy ciąg słów,
- $\operatorname{df}_S(w)$ to częstość dokumentowa słowa $w$ w kolekcji $S$, tzn. odpowiedź na pytanie, w ilu dokumentach występuje $w$.
Rzecz jasna, ten sposób ważenia oznacza tak naprawdę zastosowanie wektoryzacji tf-idf zamiast tf, nasza sieć będzie dana zatem wzorem:
$$y = \operatorname{softmax}(C\operatorname{tfidf}(w_1,\dots,w_{i-1})).$$
Bardziej skomplikowane sposoby ważenia słów
Można oczywiście połączyć odwrotną częstość dokumentową z uwzględnieniem pozycji słowa:
$$\omega(j, w_j) = \beta^{i-j-1}\operatorname{idf}_S(w_j).$$
Uwaga: „wagi” $\omega(j, w_j)$ nie są tak naprawdę wyuczalnymi wagami (parametrami) naszej sieci neuronowej, terminologia może być tutaj myląca. Z punktu widzenia sieci neuronowej $\omega(j, w_j)$ są stałe i nie są optymalizowane w procesie propagacji wstecznej. Innymi słowy, tak zdefiniowane $\omega(j, w_j)$ zależą tylko od:
- hiperparametru $\beta$, który może być optymalizowany już poza siecią (w procesie hiperoptymalizacji),
- wartości $\operatorname{idf}_S(w_j)$ wyliczanych wcześniej na podstawie kolekcji $S$.
Pytanie: czy wagi $\omega(j, w_j)$ mogłyby sensownie uwzględniać jakieś parametry wyuczalne z całą siecią?
Modelowanie języka przy użyciu bardziej złożonych neuronowych sieci _feed-forward
Można połączyć zalety obu ogólnych podejść (n-gramowego modelu i worka słów) — można równocześnie traktować w specjalny sposób (na przykład) dwa poprzedzające wyrazy, wszystkie zaś inne wyrazy reprezentować jako „tło” modelowane za pomocą worka słów lub podobnej reprezentacji. Osiągamy to poprzez konkatenację wektora poprzedzającego słowa, słowa występującego dwie pozycje wstecz oraz zagregowanego zanurzenia całego wcześniejszego tekstu:
$$y = \operatorname{softmax}(C[E(w_{i-1}),E(w_{i-2}),A(w_1,\dots,w_{i-3})]),$$
czy lepiej z dodatkową warstwą ukrytą:
$$y = \operatorname{softmax}(C\operatorname{tgh}(W[E(w_{i-1}),E(w_{i-2}),A(w_1,\dots,w_{i-3})])),$$
W tak uzyskanym dwuwarstwowym neuronowym modelu języka, łączącym model trigramowy z workiem słów, macierz $W$ ma rozmiar $h \times 3m$.
Pytanie: jakie mamy możliwości, jeśli zamiast przewidywać kolejne słowo, mamy za zadanie odgadywać słowo w luce (jak w wyzwaniach typu _word gap)?
Literatura
Skuteczny n-gramowy neuronowy model języka opisano po raz pierwszy w pracy A Neural Probabilistic Language Model autorstwa Yoshua Bengio i in.