moj-2024/wyk/12_Rekurencyjny_model_jezyka.ipynb

Modelowanie języka

12. Model języka oparty na rekurencyjnej sieci neuronowej [wykład]

Filip Graliński (2022)

Model języka oparty na rekurencyjnej sieci neuronowej

Podejście rekurencyjne

Na poprzednim wykładzie rozpatrywaliśmy różne funkcje $A(w_1,\dots,w_{i-1})$, dzięki którym możliwe było „skompresowanie” ciągu słów (a właściwie ich zanurzeń) o dowolnej długości w wektor o stałej długości.

Funkcję $A$ moglibyśmy zdefiniować w inny sposób, w sposób rekurencyjny.

Otóż moglibyśmy zdekomponować funkcję $A$ do

• pewnego stanu początkowego $\vec{s_0} \in \mathcal{R}^p$,
• pewnej funkcji rekurencyjnej $R : \mathcal{R}^p \times \mathcal{R}^m \rightarrow \mathcal{R}^p$.

Wówczas funkcję $A$ można będzie zdefiniować rekurencyjnie jako:

$$A(w_1,\dots,w_t) = R(A(w_1,\dots,w_{t-1}), E(w_t)),$$

przy czym dla ciągu pustego:

$$A(\epsilon) = \vec{s_0}$$

Przypomnijmy, że $m$ to rozmiar zanurzenia (embeddingu). Z kolei $p$ to rozmiar wektora stanu (często $p=m$, ale nie jest to konieczne).

Przy takim podejściu rekurencyjnym wprowadzamy niejako „strzałkę czasu”, możemy mówić o przetwarzaniu krok po kroku.

W wypadku modelowania języka możemy końcowy wektor stanu zrzutować do wektora o rozmiarze słownika i zastosować softmax:

$$\vec{y} = \operatorname{softmax}(CA(w_1,\dots,w_{i-1})),$$

gdzie $C$ jest wyuczalną macierzą o rozmiarze $|V| \times p$.

Worek słów zdefiniowany rekurencyjnie

Nietrudno zdefiniować model „worka słów” w taki rekurencyjny sposób:

• $p=m$,
• $\vec{s_0} = [0,\dots,0]$,
• $R(\vec{s}, \vec{x}) = \vec{s} + \vec{x}.$

Dodawanie (również wektorowe) jest operacją przemienną i łączną, więc to rekurencyjne spojrzenie niewiele tu wnosi. Można jednak zastosować inną funkcję $R$, która nie jest przemienna — w ten sposób wyjdziemy poza nieuporządkowany worek słów.

Związek z programowaniem funkcyjnym

Zauważmy, że stosowane tutaj podejście jest tożsame z zastosowaniem funkcji typu fold w językach funkcyjnych:

W Pythonie odpowiednik fold jest funkcja reduce z pakietu functools:

from functools import reduce

def product(ns):
  return reduce(lambda a, b: a * b, ns, 1)

product([2, 3, 1, 3])

18

Sieci rekurencyjne

W jaki sposób „złamać” przemienność i wprowadzić porządek? Jedną z najprostszych operacji nieprzemiennych jest konkatenacja — możemy dokonać konkatenacji wektora stanu i bieżącego stanu, a następnie zastosować jakąś prostą operację (na wyjściu musimy mieć wektor o rozmiarze $p$, nie $p + m$!), dobrze przy okazji „złamać” też liniowość operacji. Możemy po prostu zastosować rzutowanie (mnożenie przez macierz) i jakąś prostą funkcję aktywacji (na przykład sigmoidę):

$$R(\vec{s}, \vec{e}) = \sigma(W[\vec{s},\vec{e}] + \vec{b}).$$

Dodatkowo jeszcze wprowadziliśmy wektor obciążeń $\vec{b}$, a zatem wyuczalne wagi obejmują:

• macierz $W \in \mathcal{R}^p \times \mathcal{R}^{p+m}$,
• wektor obciążeń $b \in \mathcal{R}^p$.

Olbrzymią zaletą sieci rekurencyjnych jest fakt, że liczba wag nie zależy od rozmiaru wejścia!

Zwykła sieć rekurencyjna

Wyżej zdefiniową sieć nazywamy „zwykłą” siecią rekurencyjną (_Vanilla RNN).

Uwaga: przez RNN czasami rozumie się taką „zwykłą” sieć rekurencyjną, a czasami szerszą klasę sieci rekurencyjnych obejmujących również sieci GRU czy LSTM (zob. poniżej).

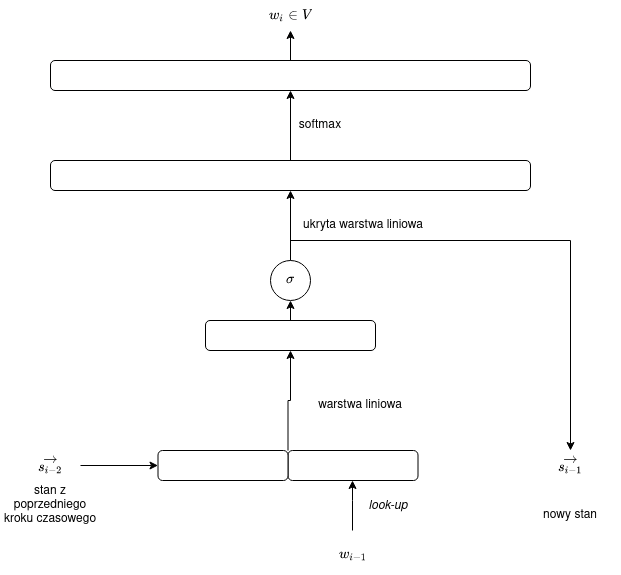
Uwaga: powyższy schemat nie obejmuje już „całego” działania sieci, tylko pojedynczy krok czasowy.

Praktyczna niestosowalność prostych sieci RNN

Niestety w praktyce proste sieci RNN sprawiają duże trudności jeśli chodzi o propagację wsteczną — pojawia się zjawisko zanikającego (rzadziej: eksplodującego) gradientu. Dlatego zaproponowano różne modyfikacje sieci RNN. Zacznijmy od omówienia stosunkowo prostej sieci GRU.

Sieć GRU

GRU (_Gated Recurrent Unit) to sieć z dwiema bramkami (gates):

• bramką resetu (_reset gate) $\Gamma_\gamma \in \mathcal{R}^p$ — która określa, w jakim stopniu sieć ma pamiętać albo zapominać stan z poprzedniego kroku,
• bramką aktualizacji (_update gate) $\Gamma_u \in \mathcal{R}^p$ — która określa wpływ bieżącego wyrazu na zmianę stanu.

Tak więc w skrajnym przypadku:

• jeśli $\Gamma_\gamma = [0,\dots,0]$, sieć całkowicie zapomina informację płynącą z poprzednich wyrazów,
• jeśli $\Gamma_u = [0,\dots,0]$, sieć nie bierze pod uwagę bieżącego wyrazu.

Zauważmy, że bramki mogą selektywnie, na każdej pozycji wektora stanu, sterować przepływem informacji. Na przykład $\Gamma_\gamma = [0,1,\dots,1]$ oznacza, że pierwsza pozycja wektora stanu jest zapominana, a pozostałe — wnoszą wkład w całości.

Wzory

Najpierw zdefiniujmy pośredni stan $\vec{\xi} \in \mathcal{R}^p$:

$$\vec{\xi_t} = \operatorname{tanh}(W_{\xi}[\Gamma_\gamma \bullet \vec{s_{t-1}}, E(w_t)] + b_{\xi}),$$

gdzie $\bullet$ oznacza iloczyn Hadamarda (nie iloczyn skalarny!) dwóch wektorów:

$$[x_1,\dots,x_n] \bullet [y_1,\dots,y_n] = [x_1 y_1,\dots,x_n y_n].$$

Jak widać, obliczanie $\vec{\xi_t}$ bardzo przypomina zwykłą sieć rekurencyjną, jedyna różnica polega na tym, że za pomocą bramki $\Gamma_\gamma$ modulujemy wpływ poprzedniego stanu.

Ostateczna wartość stanu jest średnią ważoną poprzedniego stanu i bieżącego stanu pośredniego:

$$\vec{s_t} = \Gamma_u \bullet \vec{\xi_t} + (1 - \Gamma_u) \bullet \vec{s_{t-1}}.$$

Skąd się biorą bramki $\Gamma_\gamma$ i $\Gamma_u$? Również z poprzedniego stanu i z bieżącego wyrazu.

$$\Gamma_\gamma = \sigma(W_\gamma[\vec{s_{t-1}},E(w_t)] + \vec{b_\gamma}),$$

$$\Gamma_u = \sigma(W_u[\vec{s_{t-1}},E(w_t)] + \vec{b_u}),$$

Sieć LSTM

Architektura LSTM (_Long Short-Term Memory), choć powstała wcześniej niż GRU, jest od niej nieco bardziej skomplikowana.

• zamiast dwóch bramek LSTM zawiera trzy bramki: bramkę wejścia (_input gate), bramkę wyjścia (_output gate) i bramkę zapominania (forget gate),
• oprócz ukrytego stanu $\vec{s_t}$ sieć LSTM posiada również komórkę pamięci (_memory cell), $\vec{c_t}$, komórka pamięci, w przeciwieństwie do stanu, zmienia się wolniej (intuicyjnie: _jeśli nie zrobimy nic specjalnego, wartość komórki pamięci się nie zmieni).

Wzory

Komórka pamięci modulowana jest za pomocą bramki zapominania ($\Gamma_f$) i bramki wejścia ($\Gamma_i$), bramki te określają, na ile uwzględniamy, odpowiednio, poprzednią wartość komórki pamięci $\vec{c_{t-1}}$ i wejście, a właściwie wejście w połączeniu z poprzednim stanem:

$$\vec{c_t} = \Gamma_f \bullet \vec{c_{t-1}} + \Gamma_i \bullet \vec{\xi_t},$$

gdzie wektor pomocniczy $\vec{\xi_t}$ wyliczany jest w następujący sposób:

$$\vec{\xi_t} = \operatorname{tanh}(W_{\xi}[\vec{s_{t-1}}, E(w_t)] + \vec{b_\xi}.$$

Nowa wartość stanu sieci nie zależy bezpośrednio od poprzedniej wartości stanu, lecz jest równa komórce pamięci modulowanej bramką wyjścia:

$$\vec{h_t} = \Gamma_o \bullet \operatorname{tanh}(\vec{c_t}).$$

Obliczanie bramek

Wartości wszystkie trzech bramek są liczone w identyczny sposób (wzory różnią się tylko macierzami wag i wektorem obciążeń):

$$\Gamma_f = \sigma(W_f[\vec{s_{t-1}}, E(w_t)] + \vec{b_f}),$$

$$\Gamma_i = \sigma(W_i[\vec{s_{t-1}}, E(w_t)] + \vec{b_i}),$$

$$\Gamma_o = \sigma(W_o[\vec{s_{t-1}}, E(w_t)] + \vec{b_o}).$$

Wartości początkowe

Początkowe wartości stanu i komórki pamięci mogą być ustawione na zero:

$$\vec{s_0} = \vec{0},$$

$$\vec{c_0} = \vec{0}.$$

Podsumowanie

Sieci LSTM dominowały w zagadnieniach przetwarzania języka naturalnego (ogólniej: przetwarzania sekwencji) do czasu pojawienia się architektury Transformer w 2017 roku.

Na sieci LSTM oparty był ELMo, jeden z pierwszych dużych pretrenowanych modeli języka, dostrajanych później pod konkretne zadania (na przykład klasyfikację tekstu), zob. artykuł Deep contextualized word representations. Dokładniej mówiąc, ELMo był siecią BiLSTM, połączeniem dwóch sieci, jednej działającej z lewej strony na prawą, drugiej — z prawej do lewej.