pms/moj-2024
3
2
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity
0ac61134ef
moj-2024/wyk/01_Jezyk.ipynb
Filip Gralinski 7ff8deed2c Wykład
2024-02-27 21:20:36 +01:00

19 KiB
Raw Blame History

Logo 1

Modelowanie języka

1. Język i jego zapis [wykład]

Filip Graliński (2022)

Logo 2

Język — różne perspektywy

Słowo wstępne

W matematyce istnieją dwa spojrzenia na rzeczywistość: ciągłe i dyskretne.

Otaczająca nas rzeczywistość fizyczna jest z natury ciągła (przynajmniej jeśli nie operujemy w mikroskali), lecz język jest dyskretnym wyłomem w ciągłej rzeczywistości.

Lingwistyka matematyczna

Przypomnijmy sobie definicję języka przyjętą w lingwistyce matematycznej, w kontekście, na przykład, teorii automatów.

Alfabetem nazywamy skończony zbiór symboli.

Łańcuchem (napisem) nad alfabetem $\Sigma$ nazywamy dowolny, skończony, ciąg złożony z symboli z $\Sigma$.

Językiem nazywamy dowolny, skończony bądź nieskończony, zbiór łańcuchów.

W tym formalnym ujęciu językami są na przykład następujące zbiory:

  • $\{\mathit{poniedziałek},\mathit{wtorek},\mathit{środa},\mathit{czwartek},\mathit{piątek},\mathit{sobota},\mathit{niedziela}\}$
  • $\{\mathit{ab},\mathit{abb},\mathit{abbb},\mathit{abbbb},\ldots\}$

To podejście, z jednej strony oczywiście nie do końca się pokrywa się z potocznym rozumieniem słowa _język, z drugiej kojarzy nam się z takimi narzędziami informatyki jak wyrażenia regularne, automaty skończenie stanowe czy gramatyki języków programowania.

import regex as re
rx = re.compile(r'ab+')

rx.search('żabbba').group(0)
abbb
import rstr

rstr.xeger(r'ab+')
abbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb

Ujęcie probabilistyczne

Na tym wykładzie przyjmiemy inną perspektywą, częściowo ciągłą, opartą na probabilistyce. Język będziemy definiować poprzez rozkład prawdopodobieństwa: sensownym wypowiedziom czy tekstom będziemy przypisywać stosunkowe wysokie prawdopodobieństwo, „ułomnym” tekstom — niższe (być może zerowe).

Na ogół nie mamy jednak do czynienia z językiem jako takim tylko z jego przybliżeniami, modelami (model może być lepszy lub gorszy, ale przynajmniej powinien być użyteczny…). Formalnie $M$ nazywamy modelem języka (nad skończonym alfabetem $\Sigma$), jeśli określa dyskretny rozkład prawdopodobieństwa $P_M$:

$$P_M \colon \Sigma^{*} \rightarrow [0,1].$$

Rzecz jasna, skoro mamy do czynienia z rozkładem prawdopodobieństwa, to:

$$\sum_{\alpha \in \Sigma^{*}} P_M(\alpha) = 1.$$

Jeśli $M$ ma być modelem języka polskiego, oczekiwalibyśmy, że dla napisów:

  • $z_1$ — _W tym stanie rzeczy pan Ignacy coraz częściej myślał o Wokulskim.
  • $z_2$ — _Po wypełniony zbiornik pełny i należne kwotę, usłyszała w attendant
  • $z_3$ — _xxxxyźźźźźit backspace hoooooooooop x y z

zachodzić będzie:

$$ P_M(z_1) > P_M(z_2) > P_M(z_3). $$

Pytanie Jakiej konkretnie wartości prawdopodobieństwa spodziewalibyśmy się dla zdania _Dzisiaj rano kupiłem w piekarni sześć bułek dla sensownego modelu języka polskiego?

Moglibyśmy sprowadzić tę definicję języka do tej „dyskretnej”, tzn. moglibyśmy przyjąć, że łańcuch $\alpha$ należy do języka wyznaczonego przez model $M$, jeśli $P_M(\alpha) > 0$.

Pytanie Czy moglibyśmy w ten sposób opisać język nieskończony? Czy może istnieć dyskretny rozkład prawdopodobieństwa dla nieskończonego zbioru?

Co jest symbolem?

Model języka daje rozkład prawdopodobieństwa nad zbiorem łańcuchów opartym na skończonym alfabecie, tj. zbiorze symboli. W praktyce alfabet nie musi być zgodny z potocznym czy językoznawczym rozumieniem tego słowa. To znaczy alfabet może być zbiorem znaków (liter), ale modelować język możemy też przyjmując inny typ symboli: sylaby, morfemy (cząstki wyrazów) czy po prostu całe wyrazy.

Powinniśmy przy tym pamiętać, że, koniec końców, w pamięci komputera wszelkiego rodzaju łańcuchy są zapisywane jako ciągi zer i jedynek — bitów. Omówmy pokrótce techniczną stronę modelowania języka.

Kodowanie znaków

Cóż może być prostszego od pliku tekstowego?

Ala ma kota.

Komputer nic nie wie o literach.

… w rzeczywistości operuje tylko na liczbach …

… czy raczej na zerach i jedynkach …

… a tak naprawdę na ciągłym sygnale elektrycznym …

img

… zera i jedynki są w naszej głowie …

… co jest dziwne, _naprawdę dziwne …

… ale nikt normalny się tym nie przejmuje.

Jak zakodować literę?

Zakodowanie pikseli składających się na kształtu (glyfu) litery A _oczywiście nie jest dobrym pomysłem.

img

Nie, potrzebujemy _arbitralnego kodowania dla wszystkich możliwych kształtów litery A (_w naszych głowach): A, $\mathcal{A}$, $\mathbb{A}$, $\mathfrak{A}$ powinny otrzymać ten sam kod, powiedzmy 65 (binarnie: 1000001).

ASCII

ASCII to 7-bitowy (nie 8-bitowy!) system kodowania znaków.

for code in range(40, 128):
  print(f'{code}: {chr(code)}')
40: (
41: )
42: *
43: +
44: ,
45: -
46: .
47: /
48: 0
49: 1
50: 2
51: 3
52: 4
53: 5
54: 6
55: 7
56: 8
57: 9
58: :
59: ;
60: <
61: =
62: >
63: ?
64: @
65: A
66: B
67: C
68: D
69: E
70: F
71: G
72: H
73: I
74: J
75: K
76: L
77: M
78: N
79: O
80: P
81: Q
82: R
83: S
84: T
85: U
86: V
87: W
88: X
89: Y
90: Z
91: [
92: \
93: ]
94: ^
95: _
96: `
97: a
98: b
99: c
100: d
101: e
102: f
103: g
104: h
105: i
106: j
107: k
108: l
109: m
110: n
111: o
112: p
113: q
114: r
115: s
116: t
117: u
118: v
119: w
120: x
121: y
122: z
123: {
124: |
125: }
126: ~
127: 

Jak zejść na poziom bitów?

Linux — wiersz poleceń

Linux command line:

$ echo 'Ala ma kota' > file.txt
$ hexdump -C file.txt
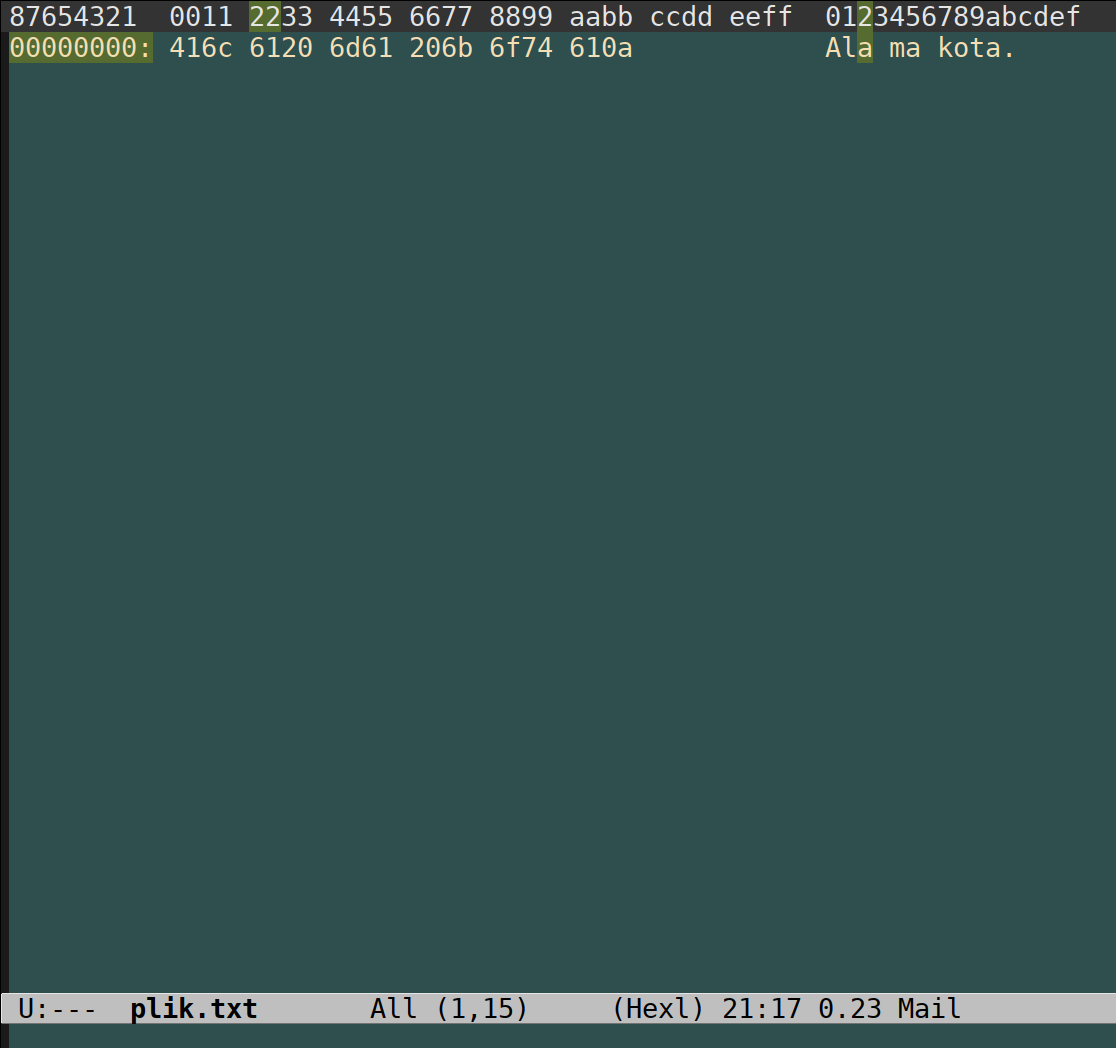
00000000  41 6c 61 20 6d 61 20 6b  6f 74 61 0a   |Ala ma kota.|
0000000c

Edytor tekstu (Emacs)

img

Uwaga!

  • kiedy dzieje się coś dziwnego, sprawdź, co tak _naprawdę jest w pliku
  • ASCII jest 7-bitowym kodowaniem (128 znaków)
    • choć zazwyczaj uzupełnionym (ang. _padded) do 8 bitów
    • nie mów plik _plik ASCII, kiedy masz na myśli prosty/czysty plik tekstowy (ang. plain text file)

Higiena plików tekstowych

Piekło końca wiersza

img

Więcej na https://re-research.pl/pl/post/2017-01-28-00042-anatomia-pliku-tekstowego-2.html

Dobre rady

  • żadnych niepotrzebnych spacji na końcu wiersza

  • żadnych niepotrzebnych pustych wierszy na końcu pliku

  • … ale ostatni wiersz powinien zakończyć się znakiem końca wiersza

  • nie używać znaków tabulacji (zamiast tego 4 spacje)

    • wyjątek: pliki TSV
    • wyjątek: pliki Makefile

  • uwaga na niestandardowe spacje i dziwne znaki o zerowej długości

Unikod

ASCII obejmuje 128 znaków: litery alfabetu łacińskiego (właściwie angielskiego), cyfry, znaki interpunkcyjne, znaki specjalne itd.

Co z pozostałymi znakami? Polskimi ogonkami, czeskimi haczykami, francuskimi akcentami, cyrylicą, koreańskim alfabetem, chińskimi znakami, rongorongo?

워싱턴, 부산, 삼성

Rozwiązaniem jest Unikod (ang. _Unicode) system, który przypisuje znakom używanym przez ludzkość liczby (kody, ang. _code points).

Znak Kod ASCII Kod Unikodowy
9 57 57
a 97 97
ą - 261
ł - 322
$\aleph$ - 1488
ặ - 7861
☣ - 9763
😇 - 128519

UTF-8

Kody znaków są pojęciem abstrakcyjnym. Potrzebujemy konkretnego kodowania by zamienić kody w sekwencję bajtów. Najpopularniejszym kodowaniem jest UTF-8.

W kodowaniu UTF-8 znaki zapisywane za pomocą 1, 2, 3, 4, 5 lub 6 bajtów (w praktyce — raczej to 4 bajtów).

Znak Kod Unikodowy Szesnastkowo UTF-8 (binarnie)
9 57 U+0049 01001001
a 97 U+0061 01100001
ą 261 U+0105 11000100:10000101
ł 322 U+0142 11000101:10000010
$\aleph$ 1488 U+05D0 11010111:10010000
ặ 7861 U+1EB7 11100001:10111010:10110111
☣ 9763 U+2623 11100010:10011000:10100011
😇 128519 U+1f607 11110000:10011111:10011000:10000111

UTF-8 — ogólny schemat zamiany kodu na bajty

  • 0x00 do 0x7F – 0xxxxxxx,
  • 0x80 do 0x7FF – 110xxxxx 10xxxxxx
  • 0x800 do 0xFFFF — 1110xxxx 10xxxxxx 10xxxxxx
  • 0x10000 do 0x1FFFFF – 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
  • 0x200000 do 0x3FFFFFF – 111110xx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
  • 0x4000000 do 0x7FFFFFFF – 1111110x 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx

Symbol x oznacza znaczący bit.

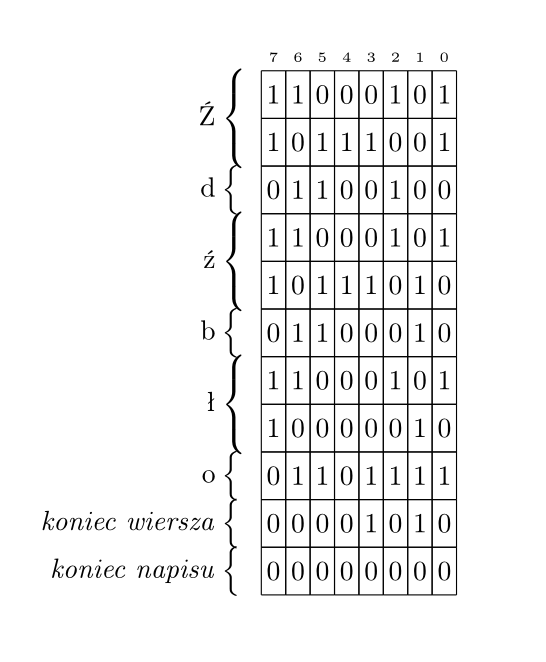
_Źdźbło to ile bajtów w UTF-8?

Jeśli wczytać jako wiersz w języku C, 11 bajtów!

img

Dlaczego UTF-8 jest doskonałym systemem kodowania?

  • wstecznie kompatybilny z ASCII
    • plik ASCII jest poprawnym plikiem UTF-8
  • nie zajmuje dużo miejsca
    • chyba że w tekście jest dużo „dziwnych” znaków
  • proste grepowanie działa
    • grep UAM text-in-utf8.txt zadziała
    • ale nawet nie próbuj: grep SRPOL text-in-utf16.txt

Porady

  • zawsze używaj UTF-8
    • bądź asertywny! jeśli w pracy każą używać czegoś innego — rezygnuj z pracy
    • NIE używaj innych unikodowych kodowań: UTF-16, UTF-32, UCS-2
    • NIE używaj nieunikodowych systemów kodowania
      • ISO-8859-2, Windows-1250, Mazovia, IEA Świerk, …
  • uwaga na pułapki UTF-8
    • ustalenie długości napisu w znakach wymaga przejścia znak po znaku
    • jeśli napis w kodowaniu UTF-8 zajmuje 9 bajtów, ile to znaków? 3, 4, 5, 6, 7, 8 lub 9!

NIE używaj sekwencji BOM

img

Unikod/UTF-8 a języki programowania

Pamiętaj, żeby być konsekwentnym!

  • kodowanie kodu źródłowego (literały!)
    • czasami podawane na początku pliku
    • … albo brane z ustawień _locale
    • … albo — domyślnie — UTF-8 (w nowszych językach programowania)
  • kodowanie standardowego wejścia/wyjścia i plików
  • jak sekwencje bajtów są interpretowane w czasie działania programu?
    • _Źdźbło jest łańcuchem złożonym z 6 czy 9 elementów??
      • 9 bajtów
      • 6 kodów
    • "Źdźbło"[1] …
      • d
      • … albo śmieci

Python 2

#!/usr/bin/python2
# -*- coding: utf-8 -*-
import sys
for line in sys.stdin:
   line = line.decode('utf-8').rstrip()
   if "źdźbło".decode('utf-8') in line:
      print len(line), ' ', line

Python3

#!/usr/bin/python3
import sys
for line in sys.stdin:
   line = line.strip()
   if "źdźbło" in line:
       print(len(line), ' ', line)

Uwaga: zakładając, że zmienna środowiskowa LANG jest ustawiona na UTF-8.