12 KiB
Klasyfikacja w Pythonie
zad. 1 Które z poniższych problemów jest problemem regresji, a które klasyfikacji?
Sprawdzenie, czy wiadomość jest spamem.
Przewidzenie oceny (od 1 do 5 gwiazdek) na podstawie komentarza.
OCR cyfr: rozpoznanie cyfry z obrazka.
Jeżeli problem jest klasyfikacyjny, to jakie mamy klasy?
Miary dla klasyfikacji
Istnieje wieje miar (metryk), na podstawie których możemy ocenić jakość modelu. Podobnie jak w przypadku regresji liniowej potrzebne są dwie listy: lista poprawnych klas i lista predykcji z modelu. Najpopularniejszą z metryk jest trafność, którą definiuje się w następujący sposób: $$ACC = \frac{k}{N}$$
gdzie:
- $k$ to liczba poprawnie zaklasyfikowanych przypadków,
- $N$ liczebność zbioru testującego.
zadanie Napisz funkcję, która jako parametry przyjmnie dwie listy (lista poprawnych klas i wyjście z klasyfikatora) i zwróci trafność.
def accuracy_measure(true, predicted):
pass
true_label = [1, 1, 1, 0, 0]
predicted = [0, 1, 0, 1, 0]
print("ACC:", accuracy_measure(true_label, predicted))Klasyfikator $k$ najbliższych sąsiadów _(ang. k-nearest neighbors, KNN)
Klasyfikator KNN, który został wprowadzony na ostatnim wykładzie, jest bardzo intuicyjny. Pomysł, który stoi za tym klasyfikatorem jest bardzo prosty: Jeżeli mamy nowy obiekt do zaklasyfikowania, to szukamy wśród danych trenujących $k$ najbardziej podobnych do niego przykładów i na ich podstawie decydujemy (np. biorąc większość) do jakie klasy powinien należeć dany obiekt.
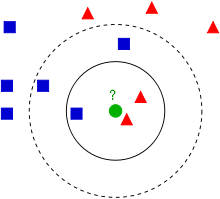
** Przykład 1** Mamy za zadanie przydzielenie obiektów do dwóch klas: trójkątów lub kwadratów. Rozpatrywany obiekt jest zaznaczony zielonym kółkiem. Przyjmując $k=3$, mamy wśród sąsiadów 2 trójkąty i 1 kwadrat. Stąd obiekt powinienm zostać zaklasyfikowany jako trójkąt. Jak zmienia się sytuacja, gdy przyjmiemy $k=5$?
Herbal Iris
_Herbal Iris jest klasycznym zbiorem danych w uczeniu maszynowym, który powstał w 1936 roku. Zawiera on informacje na 150 egzemplarzy roślin, które należą do jednej z 3 odmian.
zad. 2 Wczytaj do zmiennej data zbiór _Herbal Iris, który znajduje się w pliku iris.data. Jest to plik csv.
zad. 3 Odpowiedz na poniższe pytania:
- Które atrybuty są wejściowe, a w której kolumnie znajduje się klasa wyjściowa?
- Ile jest różnych klas? Wypisz je ekran.
- Jaka jest średnia wartość w kolumnie
sepal_length? Jak zachowuje się średnia, jeżeli policzymy ją dla każdej z klas osobno?
Wytrenujmy klasyfikator _KNN, ale najpierw przygotujmy dane. Fukcja train_test_split dzieli zadany zbiór danych na dwie części. My wykorzystamy ją do podziału na zbiór treningowy (66%) i testowy (33%), służy do tego parametr test_size.
from sklearn.model_selection import train_test_split
X = data.loc[:, 'sepal_length':'petal_width']
Y = data['class']
(train_X, test_X, train_Y, test_Y) = train_test_split(X, Y, test_size=0.33, random_state=42)
Trenowanie klasyfikatora wygląda bardzo podobnie do treningi modelu regresji liniowej:
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=3)
model.fit(train_X, train_Y)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=3, p=2,
weights='uniform')Mając wytrenowany model możemy wykorzystać go do predykcji na zbiorze testowym.
predicted = model.predict(test_X)
for i in range(10):
print("Zaklasyfikowane: {}, Orginalne: {}".format(predicted[i], test_Y.reset_index()['class'][i]))
Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor Zaklasyfikowane: Iris-setosa, Orginalne: Iris-setosa Zaklasyfikowane: Iris-virginica, Orginalne: Iris-virginica Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor Zaklasyfikowane: Iris-setosa, Orginalne: Iris-setosa Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor Zaklasyfikowane: Iris-virginica, Orginalne: Iris-virginica Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor Zaklasyfikowane: Iris-versicolor, Orginalne: Iris-versicolor
Możemy obliczyć _accuracy:
from sklearn.metrics import accuracy_score
print(accuracy_score(test_Y, predicted))0.98
zad. 4 Wytrenuj nowy model model_2 zmieniając liczbę sąsiadów na 20. Czy zmieniły się wyniki?
zad. 5 Wytrenuj model z $k=1$. Przeprowadź walidację na zbiorze trenującym zamiast na zbiorze testowym? Jakie wyniki otrzymałeś? Czy jest to wyjątek? Dlaczego tak się dzieje?
Walidacja krzyżowa
Zbiór _herbal Iris jest bardzo małym zbiorem. Wydzielenie z niego zbioru testowego jest obciążone dużą wariancją wyników, tj. w zależności od sposoby wyboru zbioru testowego wyniki mogą się bardzo różnic. Żeby temu zaradzić, stosuje się algorytm walidacji krzyżowej. Algorytm wygląda następująco:
Podziel zbiór danych na $n$ części (losowo).
Dla każdego i od 1 do $n$ wykonaj:
Weź $i$-tą część jako zbiór testowy, pozostałe dane jako zbiór trenujący.
Wytrenuj model na zbiorze trenującym.
Uruchom model na danych testowych i zapisz wyniki.
Ostateczne wyniki to średnia z $n$ wyników częściowych.
W Pythonie służy do tego funkcja
cross_val_score, która przyjmuje jako parametry (kolejno) model, zbiór X, zbiór Y. Możemy ustawić parametrcv, który określa na ile części mamy podzielić zbiór danych oraz parametrscoringokreślający miarę.W poniższym przykładzie dzielimy zbiór danych na 10 części (10-krotna walidacja krzyżowa) i jako miarę ustawiany celność (ang. accuracy).
from sklearn.model_selection import cross_val_score
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, Y, cv=10, scoring='accuracy')
print("Wynik walidacji krzyżowej:", scores.mean())zad. 6 Klasyfikator $k$ najbliższych sąsiadów posiada jeden parametr: $k$, który określa liczbę sąsiadów podczas klasyfikacji. Jak widzieliśmy, wybór $k$ może mieć duże znaczenie dla jakości klasyfikatora. Wykonaj:
- Stwórz listę
neighborswszystkich liczb nieparzystych od 1 do 50. - Dla każdego elementu
iz listyneighborszbuduj klasyfikator _KNN o liczbie sąsiadów równeji. Nastepnie przeprowadz walidację krzyżową (parametry takie same jak powyżej) i zapisz wyniki do tablicycv_scores. - Znajdź
k, dla którego klasyfikator osiąga najwyższy wynik.
Wykres przedstawiający precent błedów w zależnosci od liczby sąsiadów.
import matplotlib.pyplot as plt
# changing to misclassification error
MSE = [1 - x for x in cv_scores]
# plot misclassification error vs k
plt.plot(neighbors, MSE)
plt.xlabel('Liczba sąsiadów')
plt.ylabel('Procent błędów')
plt.show()Przejdź teraz do arkusza z zadaniem domowym, gdzie zastosujemy klasyfikator _kNN na zbiorze danych z pierwszych zajęć.