kerreg-MPSKICB/kernel_regression.ipynb

Regresja jądrowa

Karolina Oparczyk, Tomasz Grzybowski, Jan Nowak

Regresja jądrowa używana jest jako funkcja wagi do opracowania modelu regresji nieparametrycznej. Nadaje ona niektórym elementom zbioru większą "wagę", która ma wpływ na ostateczny wynik.

Można ją porównać do rysowania krzywej na wykresie punktowym tak, aby była jak najlepiej do nich dopasowana.

Właściwości regresji jądrowej:

• symetryczna - wartość maksymalna leży pośrodku krzywej
• powierzchnia pod krzywą funkcji wynosi 1
• wartość funkcji jądrowej nie jest ujemna

Do implementacji regresji jądrowej można użyć wielu różnych jąder. Przykłady użyte w projekcie:

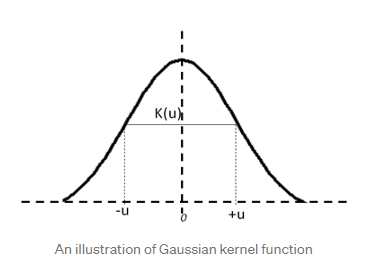
• jądro Gaussa \begin{equation} K(x) = \frac1{h\sqrt{2\pi}}e^{-\frac12(\frac{x - x_i}h)^2} \end{equation}

import KernelRegression
import plotly.express as px
import numpy as np
kernel_x = np.arange(-4,4,0.1)
col = KernelRegression.kernel_function(1, kernel_x, 0)
px.line(x=kernel_x, y=col, title='Funkcja jądrowa Gaussa')

• jądro Epanechnikova \begin{equation} K(x) = (\frac34)(1-(\frac{x - x_i}h)^2) \text{ dla } {|x|\leq1} \end{equation}

kernel_x = np.arange(-2,2,0.1)
col = KernelRegression.epanechnikov_list(1, kernel_x, 0)
px.line(x=kernel_x, y=col, title='Funkcja jądrowa Epanechnikova')

Istotne znaczenie ma nie tylko dobór jądra, ale również parametru wygładzania, czyli szerokości okna. W zależności od niego, punkty są grupowane i dla każdej grupy wyliczana jest wartość funkcji. Jeśli okno będzie zbyt szerokie, funkcja będzie bardziej przypominała prostą (under-fitting). Natomiast jeśli będzie zbyt wąskie, funkcja będzie za bardzo "skakać" (over-fitting).

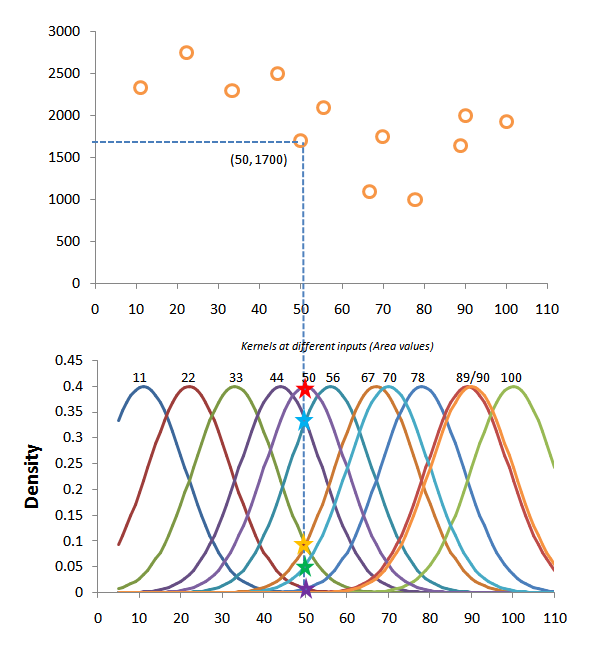
Wyliczenie wartości funkcji polega na wzięciu średniej ważonej z $y_{i}$ dla takich $x_{i}$, które znajdują się blisko x, dla którego wyznaczamy wartość. Wagi przy $y_{i}$ dla x sumują się do 1 i są wyższe, kiedy $x_{i}$ jest bliżej x oraz niższe w przeciwnym przypadku.

\begin{equation}w_i= \frac{K_i}{\sum\limits_{i=1}^n K_i} \end{equation}

\begin{equation} Y=w_1*x_1+w_2*x_2+ \text{...} +w_n*x_n \end{equation}

import ipywidgets as widgets
import plotly.graph_objs as go
import pandas as pd 

fires_thefts = pd.read_csv('fires_thefts.csv', names=['x','y'])
fires_thefts=fires_thefts.sort_values('x')
XXX = np.array(fires_thefts.x)
YYY = np.array(fires_thefts.y)

dropdown_bw = widgets.Dropdown(options=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10], value=1, description='Szerokość okna')

def interactive_kernel(bw_manual):    
    Y_pred_gauss = KernelRegression.ker_reg(XXX, YYY, bw_manual, 'gauss')
    Y_pred_epanechnikov = KernelRegression.ker_reg(XXX, YYY, bw_manual, 'epanechnikov')

    fig = px.scatter(x=XXX,y=YYY)
    fig.add_trace(go.Scatter(x=XXX, y=np.array(Y_pred_gauss), name='Gauss',  mode='lines'))
    fig.add_trace(go.Scatter(x=XXX, y=np.array(Y_pred_epanechnikov), name='Epanechnikov',  mode='lines'))
    fig.show()
    
    # kernel regression
    kernel_x = np.arange(min(XXX)-5,max(XXX)+5, 0.1)

    ## Plotting gaussian for all input x points 
    kernel_fns = {'kernel_x': kernel_x}
    for input_x in XXX: 
        input_string= 'x_value_{}'.format(np.round(input_x,2)) 
        kernel_fns[input_string] = KernelRegression.kernel_function(bw_manual, kernel_x, input_x)

    kernels_df = pd.DataFrame(data=kernel_fns)
    y_all = kernels_df.drop(columns='kernel_x')
    fig = px.line(kernels_df, x='kernel_x', y=y_all.columns, title='Gaussian for all input points', range_x=[min(XXX)-5,max(XXX)+5])    
    fig.show()

widgets.interact(interactive_kernel, bw_manual=dropdown_bw)

interactive(children=(Dropdown(description='Szerokość okna', options=(1, 2, 3, 4, 5, 6, 7, 8, 9, 10), value=1)…

<function __main__.interactive_kernel(bw_manual)>

bw_manual = 3
input_x = XXX[37]
kernel_x = XXX
weigths = KernelRegression.weights(bw_manual, input_x, XXX)
# Dataframe for a single observation point x_i. In the code x_i comes from new_x
data = {'Input_x': [input_x for x in kernel_x],
        'kernel_x': kernel_x,
        'weigth': weigths,
        'Y': YYY,
        'Y=w0*x0+w1*x1+...+w41*x41': ''
        }
single_pt_KE = pd.DataFrame(data=data)
single_pt_KE.at[len(YYY)//2, 'Y=w0*x0+w1*x1+...+w41*x41'] = sum([weigths[index]*YYY[index] for index, x in enumerate(kernel_x)])
single_pt_KE['weigth'] = single_pt_KE['weigth'].map('{:,.10f}'.format)
single_pt_KE['kernel_x'] = single_pt_KE['kernel_x'].map('K({})'.format)
single_pt_KE

	Input_x	kernel_x	weigth	Y	Y=w0*x0+w1*x1+...+w41*x41
0	28.6	K(2.0)	0.0000000000	11
1	28.6	K(2.2)	0.0000000000	9
2	28.6	K(2.2)	0.0000000000	14
3	28.6	K(2.5)	0.0000000000	22
4	28.6	K(3.4)	0.0000000000	17
5	28.6	K(3.6)	0.0000000000	15
6	28.6	K(4.0)	0.0000000000	16
7	28.6	K(4.8)	0.0000000000	19
8	28.6	K(5.0)	0.0000000000	32
9	28.6	K(5.4)	0.0000000000	27
10	28.6	K(5.6)	0.0000000000	23
11	28.6	K(5.7)	0.0000000000	11
12	28.6	K(6.2)	0.0000000000	29
13	28.6	K(6.9)	0.0000000000	18
14	28.6	K(7.2)	0.0000000000	29
15	28.6	K(7.3)	0.0000000000	31
16	28.6	K(7.7)	0.0000000000	37
17	28.6	K(8.6)	0.0000000001	53
18	28.6	K(9.0)	0.0000000002	39
19	28.6	K(9.5)	0.0000000006	44
20	28.6	K(10.5)	0.0000000048	42
21	28.6	K(10.5)	0.0000000048	36	32.501314
22	28.6	K(10.7)	0.0000000072	43
23	28.6	K(10.8)	0.0000000088	34
24	28.6	K(11.0)	0.0000000131	75
25	28.6	K(11.3)	0.0000000233	34
26	28.6	K(11.9)	0.0000000725	46
27	28.6	K(12.2)	0.0000001259	46
28	28.6	K(15.1)	0.0000155643	25
29	28.6	K(15.1)	0.0000155643	30
30	28.6	K(16.5)	0.0001139880	40
31	28.6	K(17.4)	0.0003654367	32
32	28.6	K(18.4)	0.0011998863	32
33	28.6	K(18.5)	0.0013431325	22
34	28.6	K(21.6)	0.0255338383	31
35	28.6	K(21.8)	0.0297651397	4
36	28.6	K(23.3)	0.0815871059	29
37	28.6	K(28.6)	0.3884742117	27
38	28.6	K(29.1)	0.3831160323	34
39	28.6	K(34.1)	0.0723612716	68
40	28.6	K(36.2)	0.0156949327	41
41	28.6	K(39.7)	0.0004136342	147

from sklearn.linear_model import LinearRegression
# linear regression
reg = LinearRegression().fit(XXX.reshape(-1, 1), YYY.reshape(-1, 1))
Y_pred_linear = reg.predict(XXX.reshape(-1, 1))

# kernel regression
Y_pred_gauss = KernelRegression.ker_reg(XXX, YYY, bw_manual, 'gauss')
Y_pred_epanechnikov = KernelRegression.ker_reg(XXX, YYY, bw_manual, 'epanechnikov')

fig = px.scatter(x=XXX,y=YYY)
fig.add_trace(go.Scatter(x=XXX, y=np.array(Y_pred_gauss), name='Gauss',  mode='lines'))
fig.add_trace(go.Scatter(x=XXX, y=np.array(Y_pred_epanechnikov), name='Epanechnikov',  mode='lines'))
fig.add_trace(go.Scatter(x=XXX, y=np.array(Y_pred_linear.flatten().tolist()), name='Linear',  mode='lines'))