Przygotowali

Wojciech Jarmosz
Michał Kubiak
Przemysław Owczarczyk

Temat:

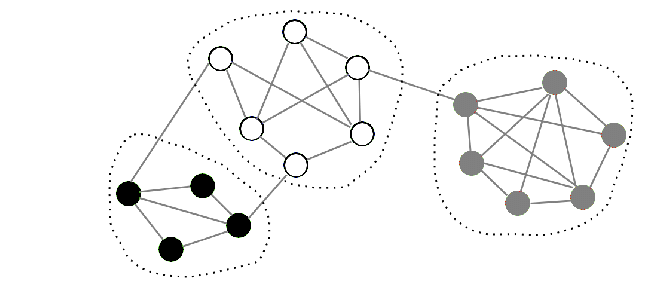
Spacery losowe po grafach: algorytm wyszukiwania klastrów. Dla dużych grafów istotną informacją jest wykrycie podgrafów, które są silnie ze sobą powiązane. Za pomocą spacerów losowych po grafach zaprojektuj algorytm, który odkrywa strukturę klastrów w grafie (clustering algorithm). Wykorzystaj swój algorytm do wskazania krytycznych wierzchołków, tj. wierzchołków, których usunięcie rozspójnia graf. Przeanalizuj wariant algorytmu dla grafów skierowanych i grafów nieskierowanych.

Wstęp

W tym projekcie opiszemy i przedstawimy skuteczny algorytm grupowania oparty na grafach, zwany grupowaniem Markowa. Podobnie jak inne algorytmy klastrowania oparte na grafach i w przeciwieństwie do klastrowania K- średnich, algorytm ten nie wymaga wcześniejszej znajomości liczby klastrów. Algorytm ten jest bardzo popularny w klastrowaniu danych bioinformatycznych, w szczególności do klastrowania sekwencji białek i klastrowania genów. Algorytm ten nadaje się również do obliczeń rozproszonych.

Spacery losowe

Spacery losowe są podstawą algorytmu MCL.
Poruszając się losowo od węzła do węzła, istnieje większe prawdopodobieństwo poruszania się wewnątrz klastru, niż przecinania klastrów. Dzieje się tak, ponieważ z definicji klastry są wewnętrznie gęste, a są oddzielone rzadkimi regionami. W grupowaniu grafów gęstość i rzadkość definiuje się jako proporcję szczelin krawędziowych, które mają w sobie krawędzie.
Przeprowadzając spacery losowe, mamy większą szansę na znalezienie trendu gromadzenia się wierzchołków i definicji klastrów w grafie.
Spacery losowe w grafie są obliczane za pomocą łańcuchów Markowa.

Markov Chains

Przykład ilustrujący działania łańcuchów Markova:
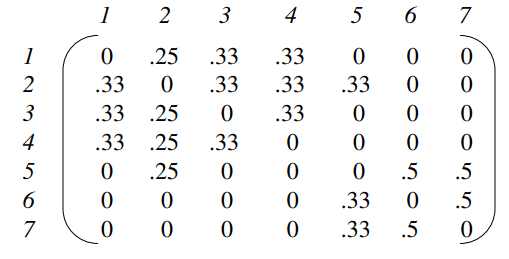
Będąc w węźlę 1 "random walker" ma 33% szansy na przejścia do węzłów 2, 3 i 4 oraz 0% do węzłów 5, 6 i 7.
Z węzła 2 ma 25% szansy na przejście do węzłów 1, 3, 4, 5 oraz 0% do węzłów 6 i 7.
Dla tego grafu macierz przejścia wygląda następująco. Można na nią patrzeć jako macierz prawdopodobieństwa, ponieważ każda kolumna sumuję się do 1.

Algorytm MCL

Korzystając z łańcuchów Markowa, rozważ dla każdej pary wezłów u i v prawdopodobieństwo rozpoczęcia od węzła u i zakończenia w węźle v po przejściu k kroków. Prawdopodobieństwo przejścia z u do v wynosi 1/u.
Znormalizuj macierz do wartości w przedziale <0,1>
Dla tak powstałej macierzy prawdopodobieństw P, obliczamy P(k) mnożąc P przez siebie k razy. (k wynosi zazwyczaj 2 lub 3). Dla początkowych potęg macierzy, poszczególne wagi połączeń będą większe w przypadku wierzchołków znajdujących się w obrębie klastra oraz niższe w przypadku połączeń pomiędzy klastrami.
Wzmocnij obserwację z poprzedniego punktu stosując tzw. inflację z parametrem r, wpływa ona na "ziarnistość" klastrów.
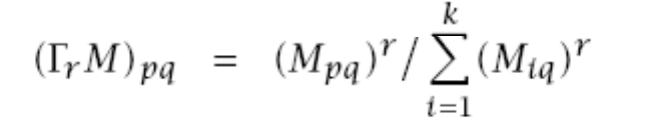
Powtarzaj kroki 3 i 4 do momentu osiągnięcia ustalonego stanu (konwergancja) - suma wartości w pojedynczej kolumnie sumuje się do tej samej liczby, w praktyce taka własność zachodzi często ale nie zawsze.
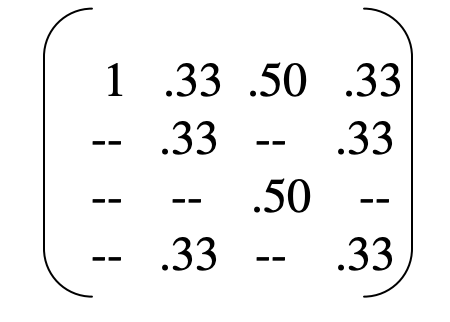
Zinterpretuj powstałą macierz w celu odkrycia klastrów. {1}, {2, 4}, {3}

4.8 KiB Raw Permalink Blame History