| .. | ||
| .RData | ||
| .Rhistory | ||
| q-q.png | ||
| README.md | ||
| test_t_dla jednej próby.pdf | ||
| zadania.R | ||
| zajecia6.Rproj | ||
| Zajęcia6.pdf | ||
Zajęcia 6
Testowanie hipotez statystycznych.
Test t-Studenta
Test t Studenta jest metodą statystyczną służącą do porównania dwóch średnich między sobą jeśli znamy liczbę badanych osób, średnią arytmetyczną oraz wartość odchylenia standardowego lub wariancji.
Jest to jeden z mniej skomplikowanych i bardzo często wykorzystywanych testów statystycznych używanych do weryfikacji hipotez. Dzięki niemu możemy dowiedzieć się czy dwie różne średnie są różne niechcący (w wyniku przypadku) czy są różne istotnie statystycznie (np. z uwagi na naszą manipulację eksperymentalna).
Są gotowe wzory do których podstawiamy wartości w zalezności od rodzaju próby.
P-wartość
P-wartość (p-value) to graniczny poziom istotności - najmniejszy, przy którym zaobserwowana wartość statystyki testowej prowadzi do odrzucenia hipotezy zerowej. Im p-wartość jest większa, tym bardziej hipoteza H0 jest prawdziwa. Im mniejsza tym niej prawdopodobna jest hipoteza H0
Wartość p, p-wartość, prawdopodobieństwo testowe.
Wykres Q-Q
Ten wykres (kwantyl - kwantyl) słuzy do porównania wartości estymowanej - na podstawie kwantyli
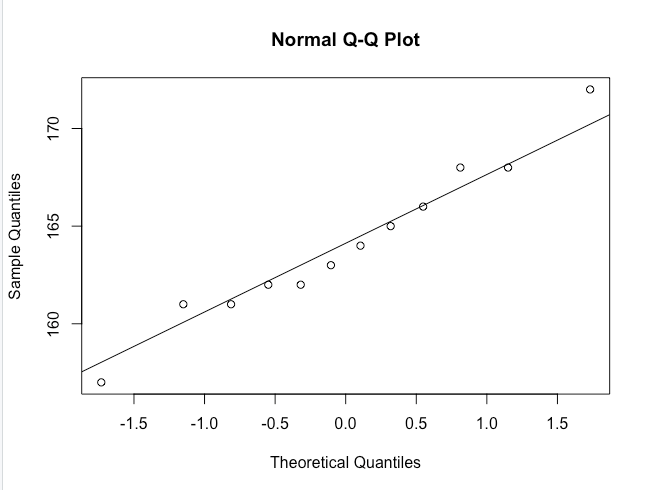
Test Shapiro-Wilka
Hipotezy:
-
H0 : Próba pochodzi z populacji o rozkładzie normalnym
-
H1 : Próba nie pochodzi z populacji o rozkładzie normalnym.
Hipoteza zerowa tego testu mówi nam o tym, że nasza próba badawcza pochodzi z populacji o normalnym rozkładzie. Jeśli test Shapiro-Wilka osiąga istotność statystyczną (p < 0,05), świadczy to o rozkładzie oddalonym od krzywej Gaussa. W przypadku tego testu najczęściej chcemy otrzymać wartości nieistotne statystyczne (p > 0,05), ponieważ świadczą one o zgodności rozkładu zmiennej z rozkładem normalnym.
Var.test
Wariancja - Intuicyjnie utożsamiana ze zróżnicowaniem zbiorowości. Wg dokumentacji jest to test pozwalający porównać wariancje z dwóch rozkładów normalnych.